一道高中数学竞赛试题的解法探究与溯源*

●宫前长　(天水市第一中学　甘肃天水　741000)



一道高中数学竞赛试题的解法探究与溯源*

●宫前长(天水市第一中学甘肃天水741000)

摘要:数学解题是数学学习的主要方式．对于有价值的典型试题，一定要弄清试题所涉及的知识点、蕴涵的思想方法和解题策略，从不同的视角进行多层次的剖析，挖掘命题的立足点，追根溯源，明确试题所要考查的知识和方法，充分展示试题探究、解法探究的作用，彰显命题人的意图和期望．

关键词:试题探究;解法探究;溯源

2015年全国高中数学联赛陕西赛区预赛试题第2试的第5题是一道有关函数、导数与恒成立交汇的题目，笔者读题、做题时发现这是一道值得探究和研究的竞赛题．现将解题方法的思考过程、试题的命制背景以及题源探究进行整理，诚请各位同仁指导!

1　问题展示

例1已知函数f(x)=xlnx，g(x)=－x2+ ax－3，其中a∈R．

(2015年全国高中数学联赛陕西赛区预赛试题)

该题目的背景是以常用的二次函数、对数函数为载体，设置为有一个参数的恒成立问题，属于常见题型．只要细心剖析，就会发现不等式中含有lnx，ex的数式结构，常常要化为和，或将lnx，ex分离出来，从而增强了不等式的等价转化．该题注重对学生逻辑思维能力的考查和数学方法的运用，融数学逻辑、方法以及操作等为一体，难度不大，却是一道具有较好区分度的试题．

2　解法探究

2．1第1)小题解法探究

第1)小题涉及含参不等式恒成立问题，是高考和竞赛持之以“恒”设问的重点，常采用函数的最值法、分离参数法、充要条件等方法来求参数的取值范围．下面只介绍分离参数法:

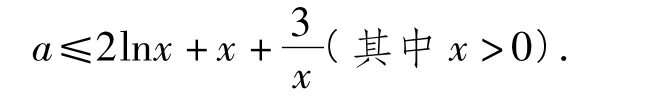
对函数h(x)求导，得

从而函数h(x)在(0，1)上单调递减，在(1，+∞)上单调递增，因此

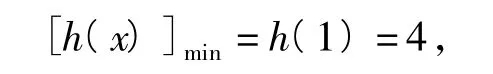
即a≤4，故a的取值范围为(－∞，4］．

2．2第2)小题解法探究

思路分析1最值法:对任意实数x∈D，函数f(x)＞g(x)恒成立等价于只需证明f(x)－g(x)＞0恒成立，即只需证明(f(x)－g(x))min＞0．有时采用中间量法:对任意实数x∈D，存在一个数M，使得函数f(x)＞g(x)恒成立等价于只需证明f(x)min≥M且M≥g(x)max成立，注意强调等号成立时x的值不同．从形的角度理解就是:要证f(x)＞g(x)成立，只要满足函数f(x)的图像始终在函数g(x)图像上方即可．

解法1对任意x∈(0，+∞)，有

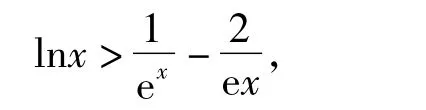
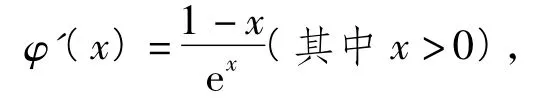
从而φ(x)在(0，1)上单调递增，在(1，+∞)上单调递减，因此

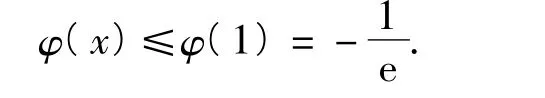
思路分析2根据重要不等式ex＞x+1(其中，得到ex－1＞x(其中x＞0)，即(其中x＞0)．再对所要证明的不等式变形、局部放缩来证明．

防治方法：由于稻蓟马很小，一般情况下，不易引起人们注意，只是当水稻严重危害而造成大量卷叶时才被发现，因此，要及时检查，把稻蓟马消灭在幼虫期。每亩用40%乐果乳剂1500～2000倍液，秧田和大田施药后，都要保持水层。防治稻蓟马后要补施速效肥，促使秧苗和分蘖恢复生长。

解法3据重要不等式ex＞x+1(其中x＞0)，得到ex－1＞x(其中x＞0)，即(其中x＞ 0)．对任意x∈(0，+∞)，要证，只要证明，此时只需要证明

点评此方法属于常规方法，将所要证明的不等式的局部进行放缩，再证明放缩后的不等式成立即可．

思路分析3结合思路分析1，2以及不等式的性质，通过放缩进行证明．根据f(x)=xlnx的性质易知:(其中x＞0)进行局部放缩，思路明了，操作方便．

点评此方法属于常规方法，根据f(x)=xlnx的性质易知:(其中x＞0)进行局部放缩，方法简捷．

思路分析4从课本习题结论出发，通过各种变形和不等式的性质来直接证明不等式成立，难度较大，容易想到，却不容易操作．

解法5易证ex＞x+1(当且仅当x=0时等号成立)．因为ex＞x+1，所以ex－1＞x，即ex≥ex，从而(当且仅当x=1时等号成立)．由(当且仅当x=1时等号成立)，得，即边取以e为底数的对数，可得，变形得(当且仅当x=时等号成立)．

点评此方法属于常规方法，容易想到教材习题的结论:1)ex＞1+x(其中x≠0);2)lnx＜x＜ex(其中x＞0)，但变形操作不容易．

3　试题溯源

这道竞赛题的第1)，2)小题其实是源于高考题，且这2个小题都涉及到课本习题．

题源1利用函数单调性，证明下列不等式: ex＞1+x(其中x≠0);lnx＜x＜ex(其中x＞0)．

(人教A版《数学(选修2-2)》习题1．3B组第1题的第3)，4)小题)

题源2已知函数f(x)=(x+1)lnx－x+1．

1)若xf'(x)≤x2+ax+1，求a的取值范围;

2)证明:(x－1)f(x)≥0．

(2010年全国数学高考理科试题第20题)

1)求a，b;

2)证明:f(x)＞1．

(2014年全国数学高考新课标卷理科试题第21题)

题源2与例1的共同特征是:对函数f(x)求导，得

原不等式xf'(x)≤x2+ax+1等价于lnx－x≤a，转化为只求得函数y=lnx－x的最大值小于a即可．只不过例1的第1)小题比高考题的外形有一些复杂，添加了心理压力，其解题的思路和方法是一样的．

题源3与例1的共同特征是:题源3通过第1)小题求得a=1，b=2后，所得函数f(x)=，对第2)小题要证明的不等式f(x)＞ 1具体化，即，通过变形处理就是所要证明的不等式:例1第2)小题给人的感觉就是将题源2进行压缩和对不等式外形进行包装、美化，比起高考题增强了外形的亲和力，更加接近学生平时熟悉的函数，其证明的入口宽，具有很好的研究价值．

通过以上对试题的解法探究、分析和背景解读，不仅挖掘出试题的源与流，而且有利于加深学生对数学知识的灵活应用，能够更全面地、深刻地理解数学概念，梳理数学知识体系和强化各个知识点之间的联系，真正做到理解数学，感悟数学!

作者简介:宫前长(1964－)，男，甘肃礼县人，中学高级教师，研究方向:中学数学教育、高考试题命制、解法研究．

修订日期:*收文日期:2015-10-13;2015-11-21．

中图分类号:O122

文献标识码:A

文章编号:1003－6407(2016)04-46-03