基本勾股数公式的一个新证法*
2016-05-10吕孙忠北京师范大学研究生院北京100875
●吕孙忠 (北京师范大学研究生院 北京 100875)
基本勾股数公式的一个新证法*
●吕孙忠(北京师范大学研究生院北京100875)
摘要:文章从三角函数的角度证明了基本勾股数公式.首先说明了一个角的正弦和余弦值同时为有理数时,该半角的正切值为有理数,接着解释了基本勾股数和单位圆上的有理点之间的关系,最后在这2个命题的基础上证明了基本勾股数公式.
关键词:基本勾股数公式;三角函数
在我国古代数学著作的《周髀算经》中,就有“勾三,股四,弦五”的原始说法,继而诞生了不定方程x2+y2=z2.人们称满足这种不定方程的正整数解(x,y,z)为勾股数.
勾股数有无数多组,并且:若(x,y,z)为勾股数,则(kx,ky,kz)也为勾股数.在这一类勾股数中找出最简单的那一组(x,y,z),其中,x,y,z两两互素,称这样的勾股数为基本勾股数[1].
基本勾股数定理[2]不定方程x2+y2=z2适合条件“x>0,y>0,z>0,(x,y)=1,x为偶数”的一切正整数解可以用下列公式表达出来:x= 2p2q2,y=p2-q2,z=p2+q2,p>q>0,(p,q)=1,且p,q一奇一偶.
分析先说明x,y,z两两互素,若(y,z)=d>1,则d|y,d|z.由x2+y2=z2,可知d|x,与(x,y)=1矛盾,故(y,z)=1,同理可推出(x,y)=(x,z)=1.于是x,y,z两两互素.下面说明x,y一奇一偶,因为(x,y)=1,所以x,y不能同时为偶数;若x,y同时为奇数,则z为偶数,此时
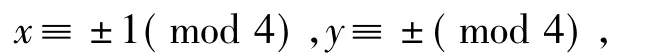
但z2≡0(mod4),这与x2+y2=z2矛盾!因此x,y一奇一偶,在定理中,不妨规定x为偶数.
再将方程x2+y2=z2变形为
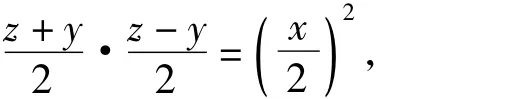
文献[2]和文献[3]分别利用了不定方程的理论和数形结合的思想证明了基本勾股数定理,具体证明请参考原文.此外,张景中院士在文献[4]中用了一种初等变形,找到了全部的基本勾股数,这种方法颇具新意,证明也较为简洁,这里对张院士的方法做简要说明.
工伤保险的目的是为了让被保人有能力再就业,使其恢复获得基本生活保障能力,保证社会持续发展,因此工伤保险的重点应是预防和康复,而不是赔偿,赔偿只是消极的事后补偿措施。目前大众对工伤保险的认识仍旧停留在补偿上,往往忽略了对工伤的预防和康复,造成终身残疾,使社会劳动力整体素质下降。
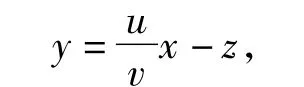
代入x2+y2=z2,整理可得
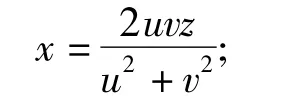
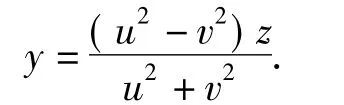
分析x,y的代数结构,使得它们成为整数,取z= (u2+v2)t,其中t为任意正整数,这样可以得到

仔细观察该式,当t=1且(u,v)=1时,所有的基本勾股数就都在这里了.
笔者在前人的研究基础之上,利用三角函数的知识,证明了基本勾股数定理.在介绍定理的证明前,先介绍2个命题.
证明根据万能公式
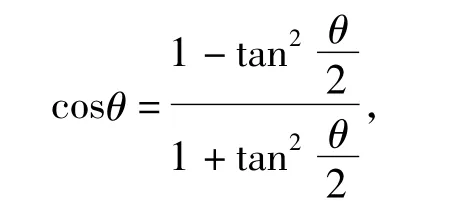
得

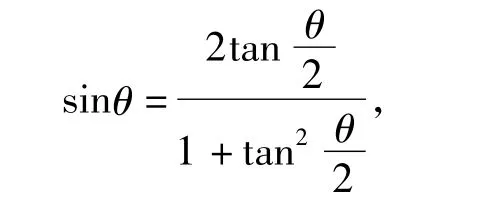
命题2所有的基本勾股数和单位圆上第一象限内所有的有理点构成一一对应的关系.
证明一方面,对于任意一组基本勾股数(x0, y0,z0),满足,它对应单位圆上第一象限内的一个点另一方面,对于第一象限内单位圆上的任意一个有理点(x1,y1),满足x21+,不妨设,其中(p1,q1)=1且 (p2,q2)=1,则
2边约去公因子,可得一组两两互素的数,这组数对应着一组基本勾股数.于是,这就建立了2者之间的一一对应关系.需要作一个假设,这里的基本勾股数,不根据奇偶性限定排序,例如(3,4,5)和(4,3,5)是2组不同的基本勾股数,它们对应的点和是圆上2个不同的点.
根据命题2可知,全部的基本勾股数和单位圆上全部的有理点之间存在着一一对应关系,换一个角度来说,如果找到了第一象限内单位圆上所有有理点的表示形式,再将它们的坐标转化为勾股数的表示形式,那么基本勾股数定理就得以证明了.沿着这条思路,展开以下证明.
命题3利用三角函数证明基本勾股数公式.
证明设(x0.y0)为第一象限内的单位圆x2+ y2=1上一个有理点,利用三角代换,可得(x0,y0)=(cosθ,sinθ),当cosθ,sinθ都为有理数时,根据命题1可知为有理数,不妨设(p0,q0)=1.因为,所以p0> q0.若p0,q0一奇一偶,则令p=p0,q=q0,代入万能公式,可得
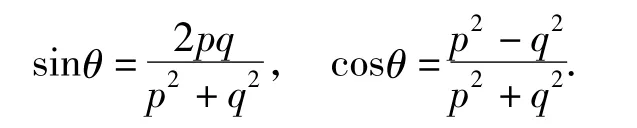
若p0,q0为2个奇数,令,则(p,q)=1,且p,q一奇一偶,代入万能公式,可得
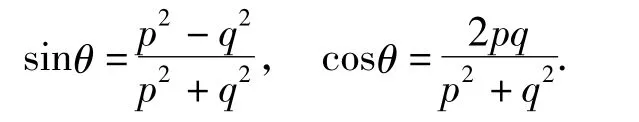
结合上述2种情况,根据命题2,这个有理点对应的基本勾股数为
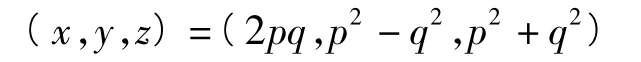
其中(p,q)=1,且p,q一奇一偶,(x,y)=1,且x,y一奇一偶.这就找到了所有的基本勾股数.若根据奇偶性调整x,y的顺序,将其中的偶数赋值给x,也就是基本勾股数定理的结论.命题3证毕..
通过以上的讨论,笔者巧用三角函数解决了基本勾股数的公式表示形式,而三角函数也有它的几何意义,有兴趣的读者可以参考文献[3]进行研究.
参考文献
[1]居复苏.勾股数,有理代换及其它[J].数学通报,1988(08):15-18.
[2]闵嗣鹤,严士健.初等数论.3版[M].北京:高等教育出版社,2005.
[3]严镇军.基本勾股数公式的几何证明[J].中学数学教学,1982(04):12-13.
[4]张景中.漫话数学[M].北京:中国少年儿童出版社,2011.
作者简介:吕孙忠(1991-),男,浙江温州人,硕士研究生,研究方向:数学教育.
修订日期:*收文日期:2015-12-07;2016-01-04.
中图分类号:O121
文献标识码:A
文章编号:1003-6407(2016)04-25-02
