例谈高中数学几种常见的命题失误*

●黄可旺　(温州第二高级中学　浙江温州　325000)



例谈高中数学几种常见的命题失误*

●黄可旺(温州第二高级中学浙江温州325000)

摘要:从当前高中数学试卷中出现的典型错例出发，剖析高中数学命题中出现的常见失误及其诱因，提醒广大教师在命题工作中既要防范出现科学性错误，也要注重试题题干语言表述简洁、规范、不产生歧义，更要关注试题设计的有效性，体现试题的公平性及对教学的导向性．

关键词:命题失误;诱因;有效性

命题是数学教师教学工作的重要环节．一个高质量的试题可帮助学生更好地掌握所学知识，理解数学思想方法．对每一位教师来说，命制出高质量的习题、试题为教学所用，是必备的基本功之一［1］．然而在实际命题过程中，因为命题者的不慎，忽视命题条件的相容性、存在性以及表意的唯一性等原则要求，导致命题失误的例子时有发生．本文以具体实例来剖析这些命题失误及其诱因，以引起教师(命题者)的注意，避免在命题中出现类似失误．

1　忽视条件间的相容性

一道数学命题应是一个有机的整体，它要求组成命题的条件与结论，以及各条件之间互相独立，且不能互相矛盾［2］．

例1已知△ABC的一个内角平分线所在的直线方程为2x+y－1=0，且顶点为A(－1，1)，B(1，2)，求顶点C的坐标．

(浙江省温州第二高级中学2015年高二期中考试试题)

分析点A(－1，1)，B(1，2)都不满足方程2x+y－1=0，因此直线2x+y－1=0是∠ACB的平分线．设点A(1，2)关于直线2x+y－1=0的对称点是A'(a，b)，则点A'在直线BC上，从而

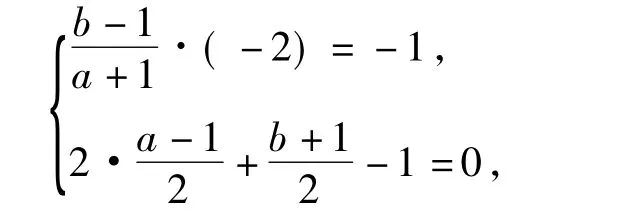
评注上述解法没有错误，但此时点A，B，C共线，这与题设“点A，B，C是△ABC的顶点”相矛盾．修正方法:调整点A(或点B)的坐标使得点A，B位于直线2x+y－1=0的2侧，且直线AB与直线2x+y－1=0相交但不垂直即可．

2　忽视几何图形的存在性

例2设△AnBnCn的3条边分别为an，bn，cn，其中n=1，2，3，……，若b1＞c1，b1+c1=2a1，，则角An的最大值是______．

(吉林省延边州2015届数学高考一模试题)

分析因为an+1=an，所以an=a1．又因为，所以

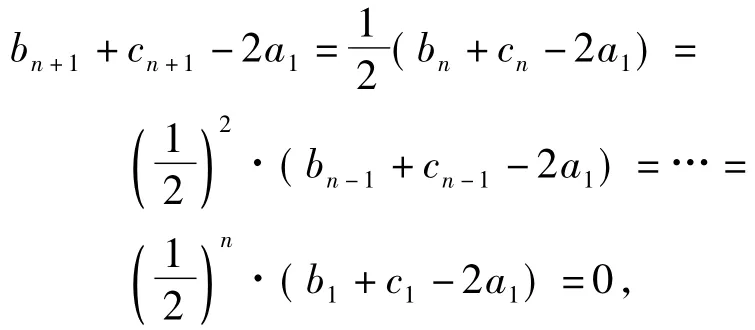
即bn+cn为常数．又由基本不等式可得

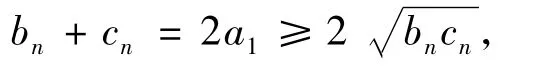
由余弦定理得

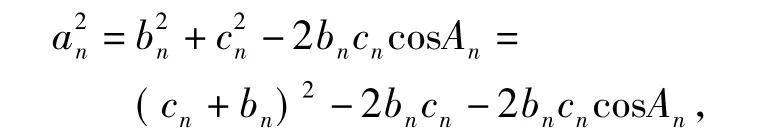
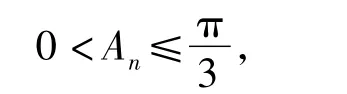
故角An的最大值是

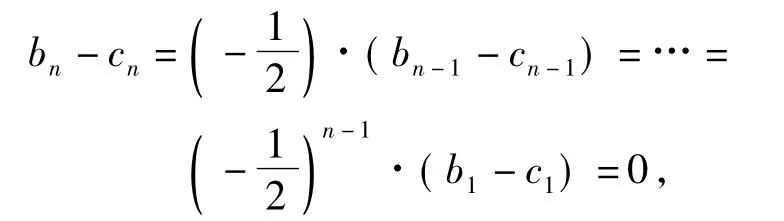
这与题干b1＞c1矛盾．故角An不存在最大值．本例出现失误的原因在于命题者未检验取得最值时三角形的存在性．若将本例的设问改为求角An的取值范围不失为一道好题．

3　混淆相近的概念

例3在△ABC中，已知AB=2AC．

1)略;

2)若AD是角A的角平分线，且AD=kAC，求k的取值范围．

(浙江省新昌中学2015年高三期中考试试题)

评注我们知道:从一个角的顶点引出一条射线，把这个角分成2个完全相同的角，这条射线叫做这个角的角平分线．由此可见，角平分线是一条射线，因此题设中点D的位置是不明确的．事实上，三角形的一个角的平分线与这个角的对边相交，联结这个角的顶点与对边交点的线段叫做三角形的角平分线(也叫三角形的内角平分线)．本例中，第2)小题应将条件修改为“若AD是角A的内角平分线”．

4　题干条件赘余

一道数学试题中各条件应当既相互独立，又缺一不可．就是说数学试题的呈现方式应符合数学学科的特征，即严谨、精确并且表述言简意赅，否则会给人造成拖沓、繁杂之感，影响考生正常作答．忽视这一原则，也会造成命题失误．

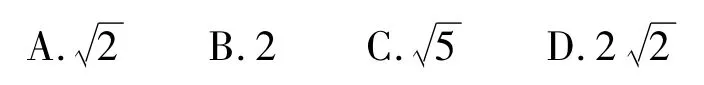
(浙江省深化课改协作校2016届高三期中联考文科试题)

分析设tanC=n，tanB=m，tan∠BAC=p，可得

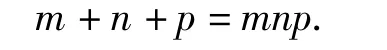
若C＞90°，n＜0＜p＜m，则m+n+p=mnp＜n，矛盾;若C＜90°，0＜p＜m＜n，则

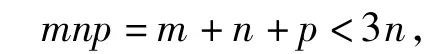
因此mp＜3．又因为m，p∈N*，所以p=1，m=2，n=3．由正弦定理可知

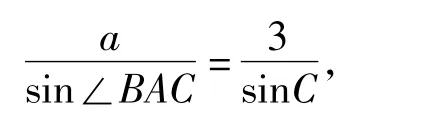
5　语义表述不清

例5某单位安排7位员工在周一至周日值班，每天一人，每人值班一天，若7位员工中的甲、乙排在相邻2天，丙不排在周一，丁不排在周日，问:有多少种安排方案?()

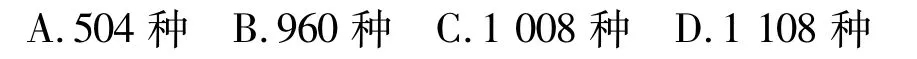
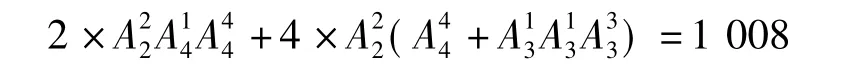
种方法．故选C．

评注若值班期限仅有一周，则答案为1008 种;若值班期限不止一周，则把甲、乙排在周日、周一，也符合相邻2天的要求，此时共有种排法，故总共有1248种排法．笔者认为本题在语言表述上存在歧义，建议将“丁不排在周日”改为“丁不排在周六”可消除歧义．

6　混淆逻辑关系

例6已知函数f(x)不是偶函数，则下列命题一定为真命题的是()

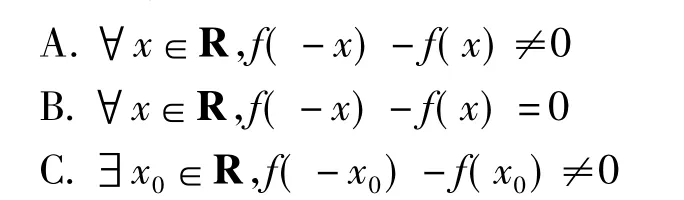
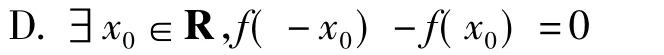
(浙江省名校新高考研究联盟2016届第一次联考理科试题)

评注本例给出的参考答案为C．本例中，若默认函数f(x)的定义域为R，则选项C，D均正确;否则，取f(x)=x，x∈［1，2］，显然此函数不是偶函数，也不存在，可见本题选项设置有误．本例错误根源在于命题者混淆了逻辑关系，误以为命题“函数f(x)是偶函数”的否定形式为事实上，命题“函数f(x)为偶函数”的全部内涵是:函数f(x)的定义域D关于原点对称且对∀x∈D，f(－x)= f(x)，故其否定形式应为“函数f(x)的定义域D不关于原点对称或∃x∈D，f(－x)≠f(x)”．修改方法:题干中增加函数f(x)的定义域为(－∞，0)∪(0，+∞)．

7　偏离考核目标

对于一道具体的试题而言，其难度的大小及在整卷中的地位在命题中必须有个清晰准确的定位．然后从“试题如何有利于学生发挥水平?如何对下一阶段的数学教与学起到良好的导向作用?试题的难度立意是否恰当?”等角度进行调整，从而使试题更趋于符合预先设定的考核目标［3］．否则，容易失去方向，人为地拔高试题难度，超出应考查的范围和难度值，将会丧失考试的公平性和对教学的导向性．

例7设函数f:N+→N+，且对所有正整数n，有f(n+1)＞f(n)，f(f(n))=3n，则f(2015)= ()

(浙江省名校新高考研究联盟2016届第一次联考理科试题)

目前，在天然药物学基础教学中，中药口袋标本已经成为学生重要的学习工具。走进药剂班，就可闻到浓浓的中药味，课间经常看见学生拿着口袋标本在认药，这对提升教学实效起到了极大的促进作用。但在应用过程中也出现了一些问题，有待改进。

分析令n=1，得f(f(1))=3;对f(1)的值进行讨论得f(1)=2，f(2)=3．当n∈N+时，

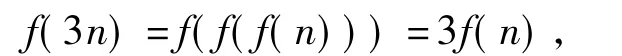
从而

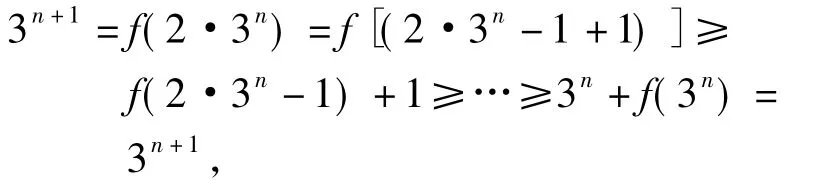
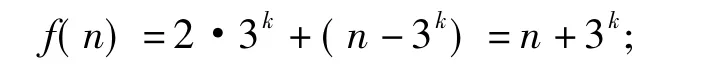
且

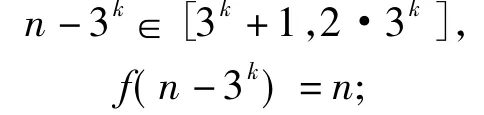
于是

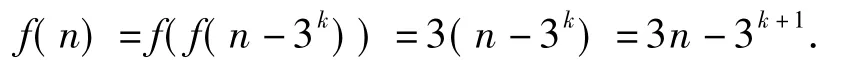
若将本题改为填空题，求f(5)的值，则不失为一道有区分度的好题．

8　忽视子题间的独立性

1)若函数g(x)与f(x)的图像关于x=1对称，求g(x)的解析式．

(第4届“睿达杯”高中生数学能力竞赛高三试题)

评注组委会公布参考答案如下:

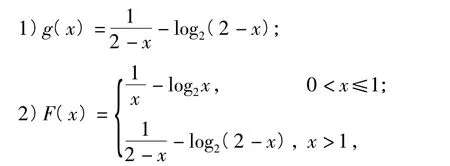
F(x)关于直线x=1对称，且F(x)在(0，1)上单调递减，在(1，2)上递增，因此

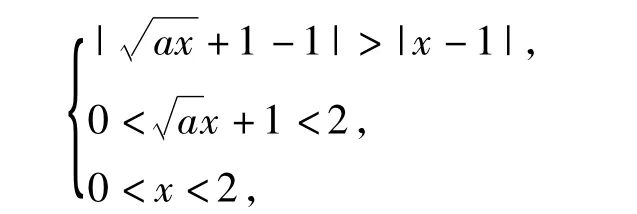
解得0≤a＜1．

我们知道，在大前提中的条件及其所推导出的结论，各子题都可用;而某个子题中的条件或推出的结论，在求解其他并列的子题时，则不能作为已知条件使用．在本例中，由第1)小题中的条件“函数g(x)与f(x)的图像关于x=1对称”得出的结论只适用第1)小题，而不适用于第2)小题．若要得到原来的解，笔者认为应把第1)小题中的条件提到大题干中，或在第2)小题中添加条件“在第1)小题的条件下”．

从上述的几个例子可以看出，虽然很多命题的错误都有一定的隐蔽，但均能找到其产生的根源．因而一道科学的数学题，必须经过命题者反复推敲，反复论证，确认没有问题后才能交给学生，不能仅凭经验，草率编题、改题．同时，教师在教学中也要引导学生辨认错题的结构及其诱因，找出修正错误的方法，从而培养其思维的批判性、严密性．

参考文献

［1］张金良．一份优质高中数学试卷的衡量标准与命制技术［J］．中学数学教育，2012(4):2-4．

［2］王从文．例说初中数学的几种命题失误［J］．中学数学教学，2001(1):36-37．

［3］董建功．如何命好数学题［M］．上海:华东师范大学出版社，2009．

作者简介:黄可旺(1981－)，男，浙江温州人，中学一级教师，教育硕士研究生，研究方向:数学教育．

修订日期:*收文日期:2015-12-19;2016-01-19．

中图分类号:O12

文献标识码:A

文章编号:1003－6407(2016)04-31-04