用本促真 贴地前行*——一道高二考题的思考历程

●李学军　(平湖中学　浙江平湖　314200)



用本促真贴地前行*——一道高二考题的思考历程

●李学军(平湖中学浙江平湖314200)

摘要:数学教师不仅要研究解题，更要研究学生的解题，引导学生用数学的思维去思考和解决问题，去体会、体验在解题过程中的纠结和成功之后的快乐，实现真正意义的数学学习．本文结合一道学生似乎无法入手的考题，展示出笔者的思考历程，得到6种解法，并进行一定的拓展．

关键词:本真;迷茫;反思;拓展

学生在做数学题的过程中，大多数是寻找曾经做过的题目的味道，对于呈现他们面前的数学试题，不能很好地思考试题的根本考点、考查的基本数学方法，当在遇到陌生的数学试题时，有时会有一种无助的感觉．当遇到暂时无法入手的试题时，我们是否真正地想到了数学学习的本质，真正想起了用数学思维去思考需要解决的问题．章建跃也曾说过:“要让学生养成‘回到概念去’思考和解决问题的习惯．”作为一线教师，笔者认为在平时的教学过程中，更应该关注数学学习的本质，用数学思维去思考数学问题．下面笔者以所任教学校2015年高二期中考试中的一道填空题为例，将这道试题的思考历程呈现如下．

例1已知实数a，b满足a2+b2≠0，过点M(－1，0)作直线ax+by+2b－a=0的垂线，垂足为N，点P(1，1)，则的最大值为______(答案:

1　不识庐山真面目——迷茫

初识此题，似乎无处着手，纠结于已知条件到底要告诉我们什么信息，因此，在这个犹豫徘徊的过程中有大量的时间从我们身边悄悄溜走，与其临渊羡渔，不如退而结网，我们完全可以从结论入手，要想求|PN|的最大值，必须要表示出|PN|，因此，非常自然就产生了如下的解法．

视角1函数思想

解法1过点M(－1，0)并且与直线ax+by+ 2b－a=0垂直的直线方程为

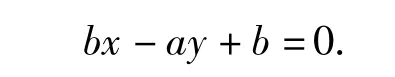
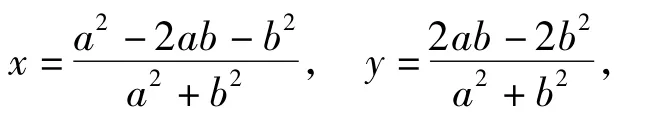
从而

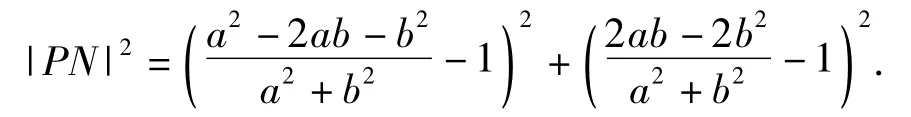
当b=0时，N(1，0)，此时|PN|=1，

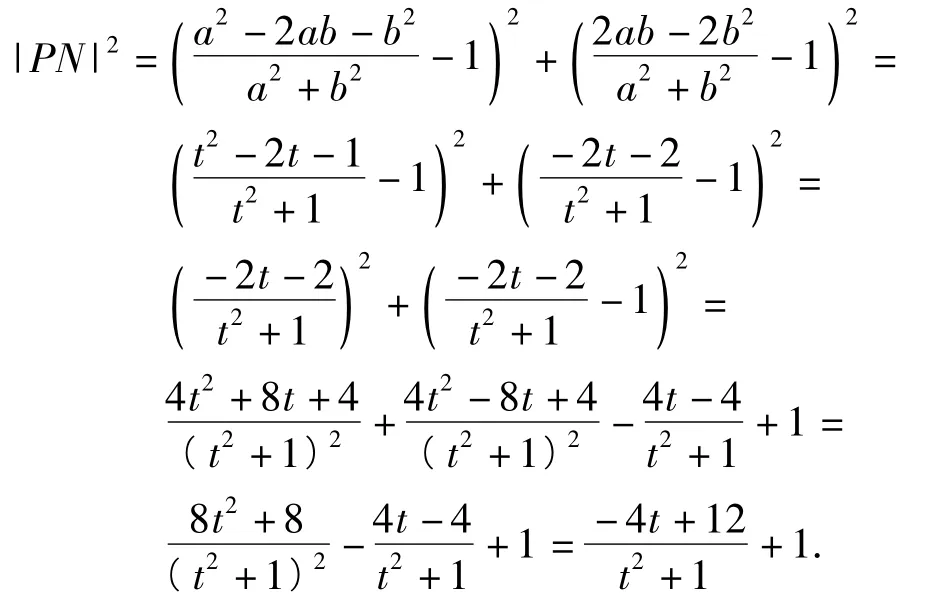
令t－3=n，则

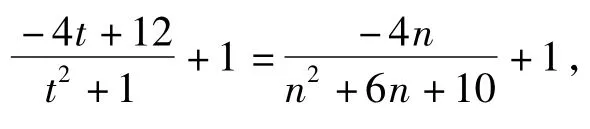
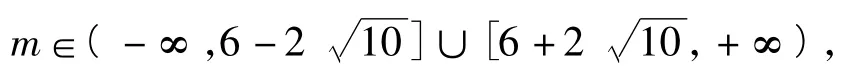
则

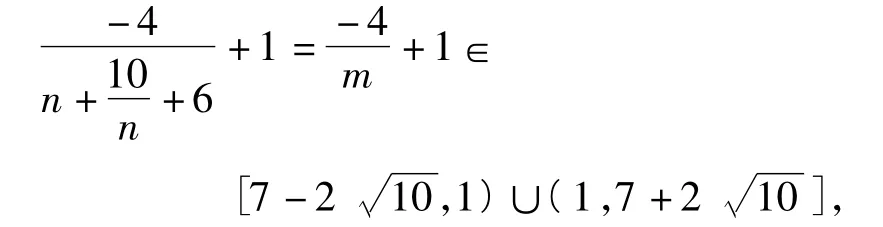
解后反思这种解法对于学生来说，“痛处”在于较大的计算量，仅仅算出点的坐标就已经让一部分学生感觉心生怯意了，接下来存在一定技巧的数据处理即二元变量到一元变量的转化也是一部分学生无法掌握并且熟练运用的，第3层操作的障碍就是函数最值的处理，总体说来这种解法对于学生来说困难重重，算对实属不易．

2　小荷才露尖尖角——清晰

在计算出|PN|2之后，发现表达式中有题目已知条件当中的a2+b2≠0，这难道是一种巧合还是另有玄机呢?这个形式却可以让我们联想到圆的方程，因此，圆的参数方程的引入的想法也就产生了，就有了如下的解法．

视角2三角函数思维

解法2令a2+b2=r2(其中r＞0)，设a= rcosθ，b=rsinθ，则

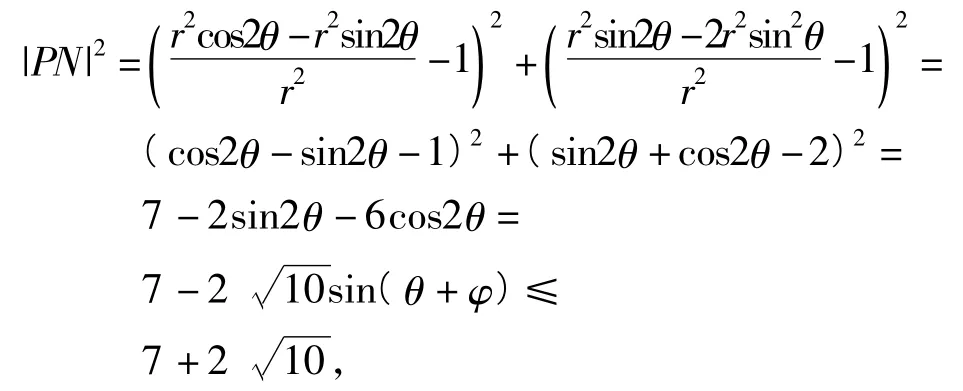
解后反思这种解法的产生来源于对圆的参数方程的深入理解及结构形式的深入认识，以及对试题中所提供的已知条件能够充分的衔接，能够很好地考查学生对于知识的理解和运用的能力，存在一定的技巧性．

视角3轨迹法

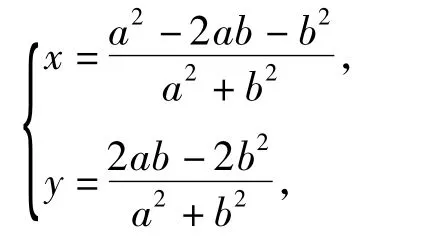
解法3事实上点N的坐标满足关系式也就是以字母a，b为参数的参数方程，如果通过消参化成普通方程，就能够比较清楚地认识点N的轨迹方程，对于研究|PN|的最大值是非常有帮助的．因为

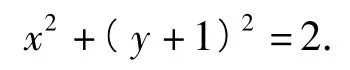
设点N(x，y)，则

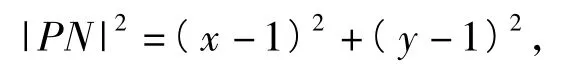
设(x－1)2+(y－1)2=m，由

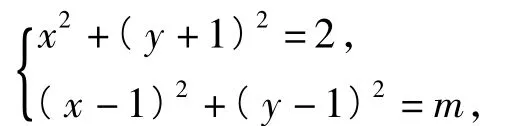
从而

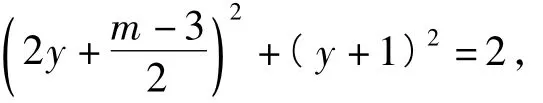
因为关于y的一元二次方程有实数根，所以

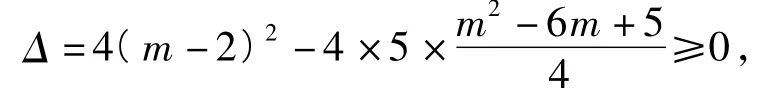
解后反思对于同样的一组数据，观察的角度不同，就会产生不一样的想法．对于已经解出的点N的坐标满足关系式

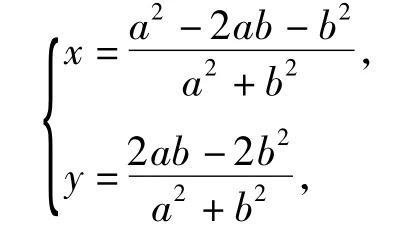
我们可以把它们看成是关于参数a，b的参数方程．但是，对于这组参数进行整体消参还是具有较大的难度，需要较高的数学综合素质．通过把参数方程转化为普通方程，就能够比较清楚地认识点N的轨迹是一个圆，然后再利用圆的相关知识进行求解．

3　横看成岭侧成峰——再思

通过上述多种方法，已经探讨出点N的轨迹方程是一个圆，那么这个问题就可以转化为圆外一点到圆上一点的距离的最大值问题，接下来利用圆的相关知识和方法对解法进行如下优化．

视角4换元法

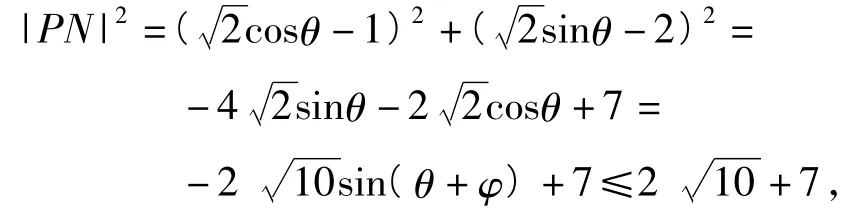
解后反思当我们已经知道点N的轨迹是一个圆的时候，就比较容易联想到圆的参数方程，从而把问题转化为求相关三角函数的最值问题．

视角五几何法

解法5如图1，设x2+(y+1)2=2的圆心C(0，－1)，直线PC交⊙C于点A，B，则

推荐理由:本书是数年难得一遇的思想巨制，是一本集经管、科普、社科、新思维于一身的作品，可以帮你化繁为简，重审世界，将世间万事的发展逻辑化作简单、可预测、可推演的规模法则。利用规模法则，不仅可以了解身体机能，甚至可以重新审视生活节奏、居住环境、就业情况以及国家的未来。本书倾注了作者在物理学、生物学、经济学、社会学等跨学科领域的毕生研究。

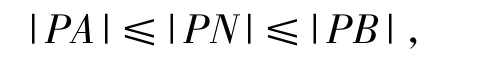
解后反思对于圆的问题一定关注圆心，利用数形结合构造三角不等式，从而能够快速地得出想要的结果．

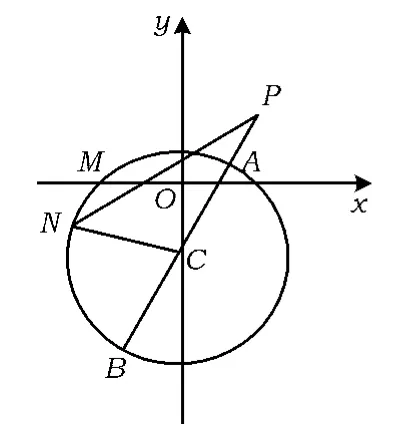
图1

图2

视角6特殊到一般

在讲评的过程中，和学生进行沟通时发现:如图2，大多数学生都已经发现了直线ax+by+2ba=0经过定点Q(1，－2)，然而学生不知道该如何利用这个定点的条件．事实上，学生在考试的过程中的确很难发现交点N的轨迹是一个圆，但是学生在思考的过程中真正缺少的却是数学思考的基本思维方式:归纳、猜想、论证．学生仅仅画出一个交点，根本就没有办法归纳出结论，但是只要多画几个交点N，然后再进行观察，直观感觉完全是可以猜测出点的轨迹有可能一个圆，然后充分利用好直角的关系，很快就可以得到点N的轨迹就是一个圆．

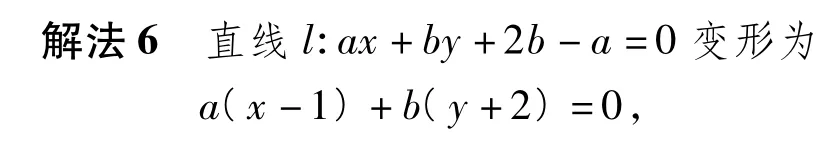
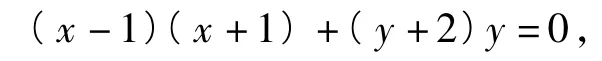
余下解法同上．

4　绝知此事要躬行——拓展

一道试题研究到这里，应该算是非常圆满了，但是似乎还有些许意犹未尽的感觉．加涅曾经说过:“问题解决并不是简单的就先前习得的规则的运用，它也是一个产生新的学习的过程．”因此，笔者尝试了进行如下拓展．

解如图3，由圆的知识知点N的轨迹是以线段QM为弦的圆所对的劣弧，QM: x+y+1=0，过线段QM的中点C的垂线方程为x－y－1=0．设圆心(t，t－1)，则

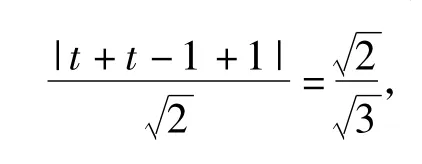
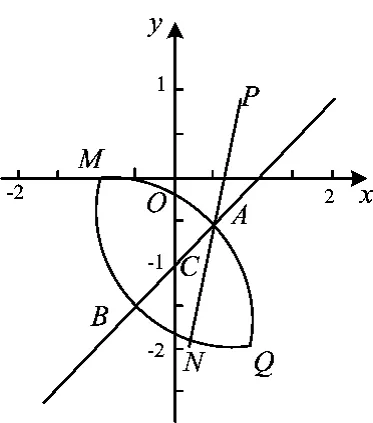
图3

求出2段圆弧所在的圆的方程分别为

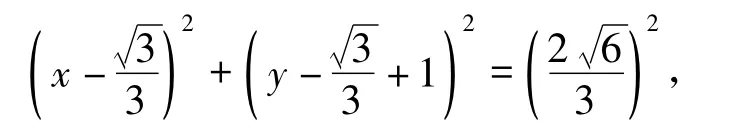
又因为

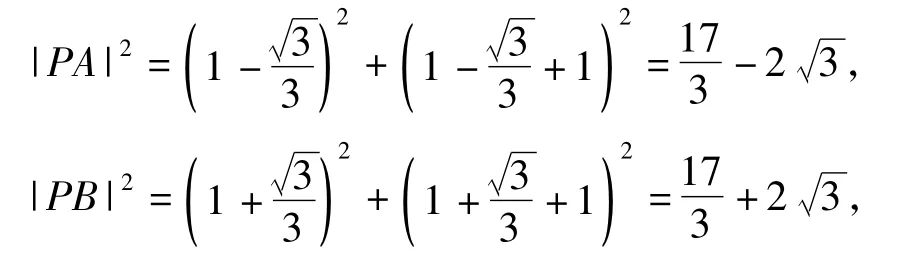
所以

解略，答案为:

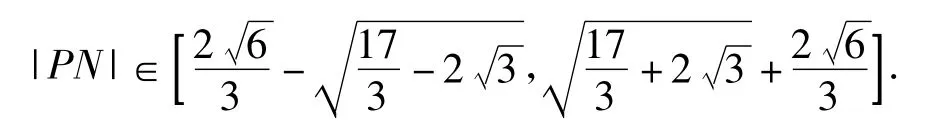
拓展3已知点M(－1，0)，点Q(1，－2)且∠QNM=α(其中0＜α＜π)，点P(1，1)，求|PN|的取值范围．

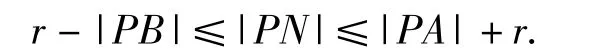
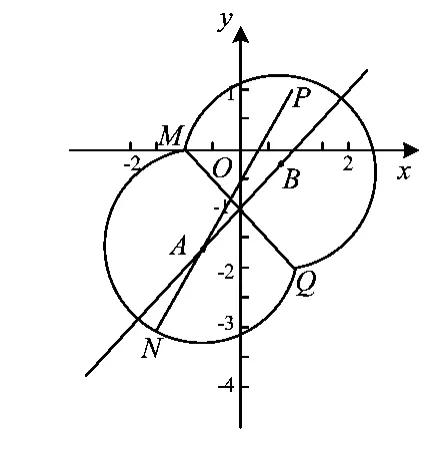
图4

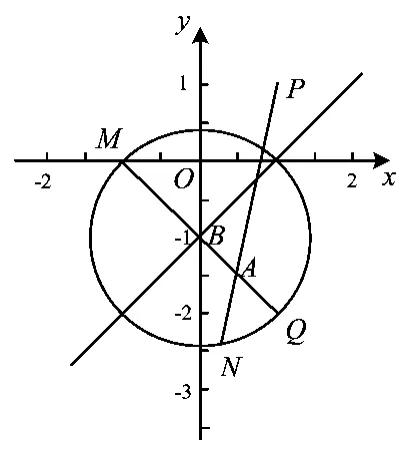
图5

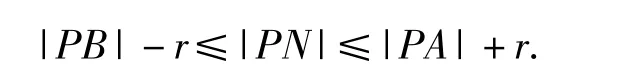
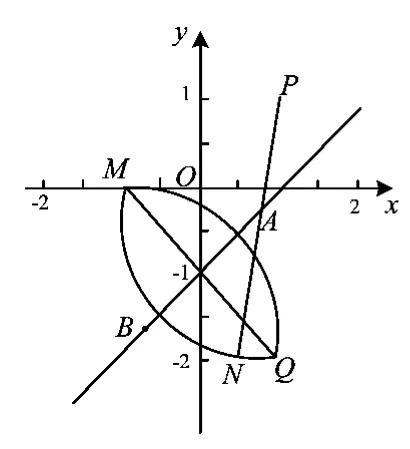
图6

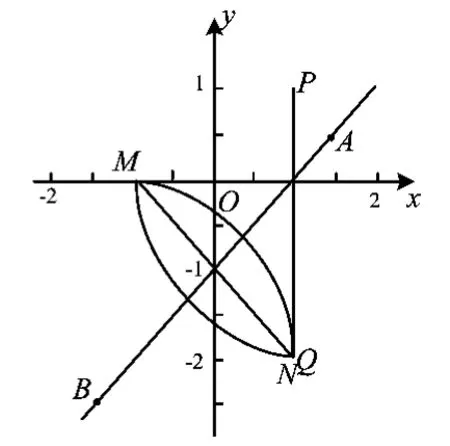
图7

4)当时(如图7)，此时点N的轨迹为以线段MQ为弦所在圆的2段劣弧，2个圆的圆心分别为A，B，此时点A的横坐标xA＞1，点B的横坐标xB＜－1，所在圆的半径为r，因此

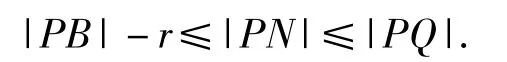
解后反思对一类问题的思考既要知其然，更要知其所以然．在思考数学问题的过程中可以将有规律的数学问题进行更深层次的挖掘、探究．这样可以遵循数学的思维方式，即由特殊到一般的思考方式，并且以问题串的方式进行呈现，问题难度由易到难，循序渐进，思维水平也是由低到高，拾阶而上．

结束语伟大数学家哈尔莫斯曾说过:“问题是数学的心脏”．数学的学习就是在不断地提出问题和解决问题的过程中发展的．波利亚也说过:“掌握数学就意味着善于解题，不仅善于解一些标准的题，而且善于解一些要求独立思考、思路合理、见解独到和有发明创造的题．”学生在数学学习的过程中，领悟基本知识、基本方法的运用，通过引导学生归纳解题方法、技巧、规律和思想方法，促进知识向能力转变，实现自我完善，争取做一题通一法，会一类通一片的效果，让我们的数学学习能够脚踏实地的“高傲”的前行．

作者简介:李学军(1976－)，男，吉林省德惠市人，中学一级教师，研究方向:数学教育．

修订日期:*收文日期:2015-12-11;2016-01-22．

中图分类号:O122

文献标识码:A

文章编号:1003－6407(2016)04-27-04