一道预赛试题的解法再探*

●邵明宪　(方城县教研室　河南方城　473200)



一道预赛试题的解法再探*

●邵明宪(方城县教研室河南方城473200)

摘要:题解研究中坚持方法服从题目的原则，注重落实通性、通法的解题理念，常可获得简单、自然的解题效果，达到揭示问题本质与展现其潜在价值的目的．

关键词:高中预赛题;不等式;探究

(2015年安徽省高中数学竞赛预赛试题第9题)

思路1(参考答案)对任意a∈(0，1)，由均值不等式，有

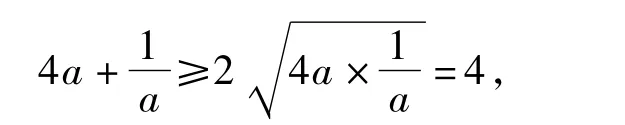
因此

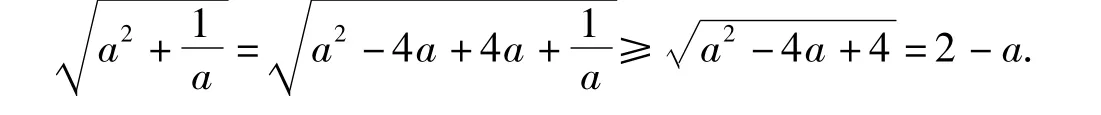
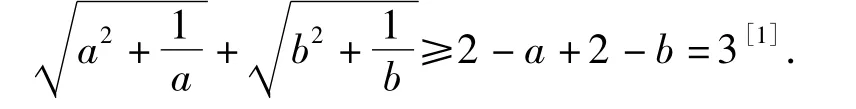
评注研读参考答案，感到其巧妙配凑似神来之笔，即使是优秀学生，多数也恐难为之．为此，笔者从注重通法，追求简单、自然的视角对该题作了探究，发现它是入手容易、走得灵活的典型范例．根据整体优先意识，易得到以下2种思路．

思路2(平方转化)

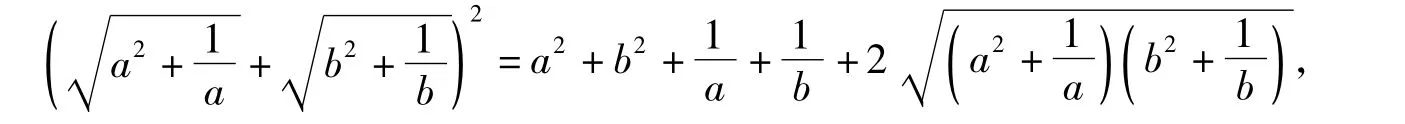
依题设及基本不等式

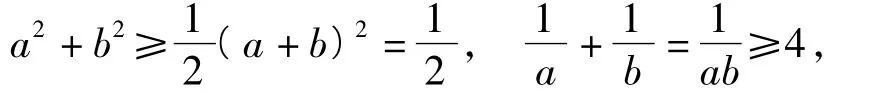
得

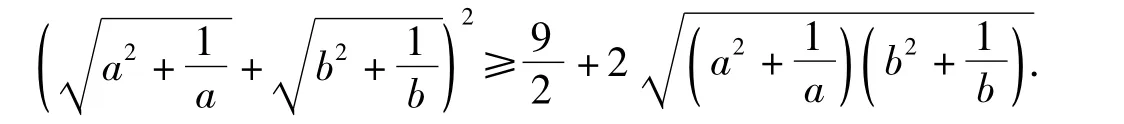
思路3(直接用均值不等式)

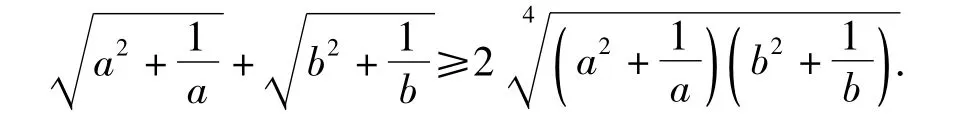
途径1利用均值不等式

1)

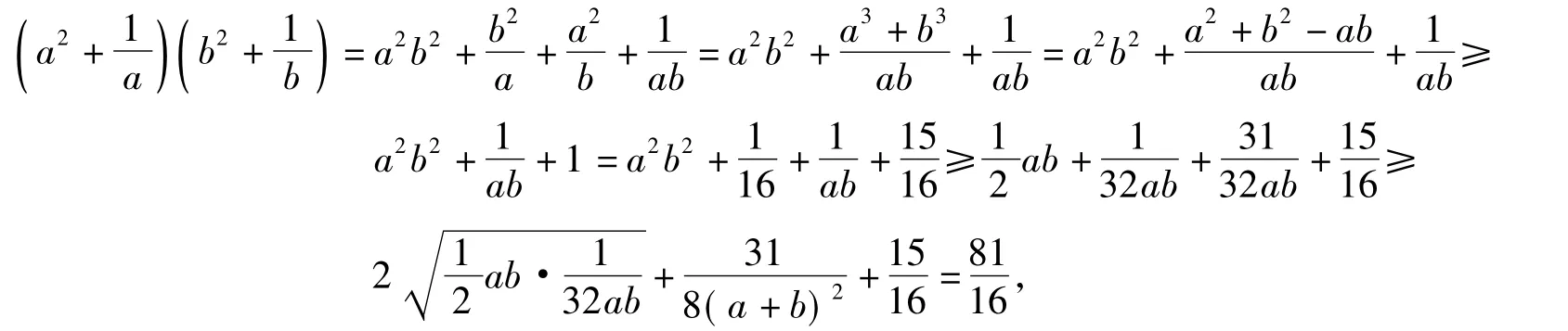
或

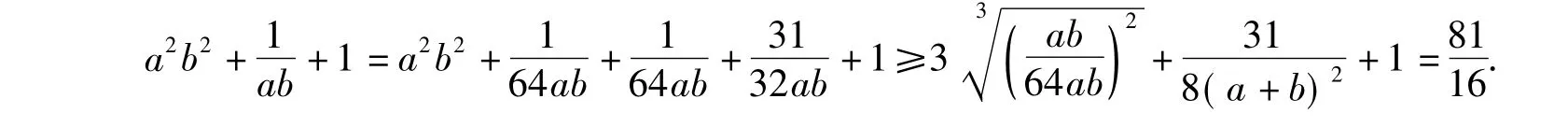
2)当0＜x＜1时，

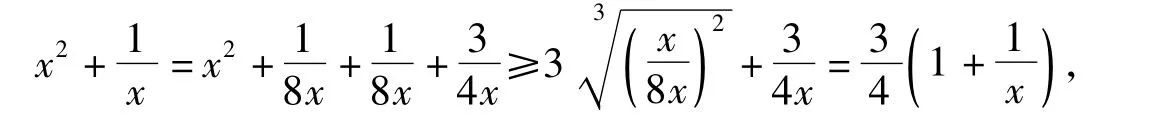
故

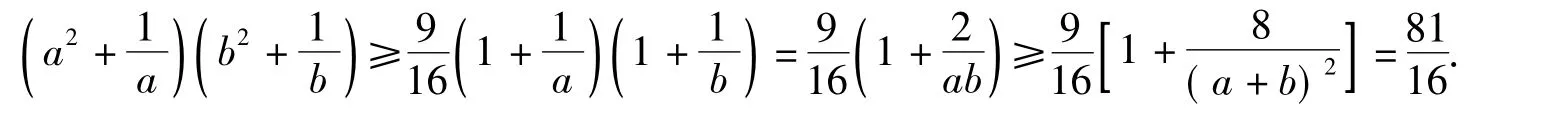
途径2同用柯西不等式和均值不等式

1)

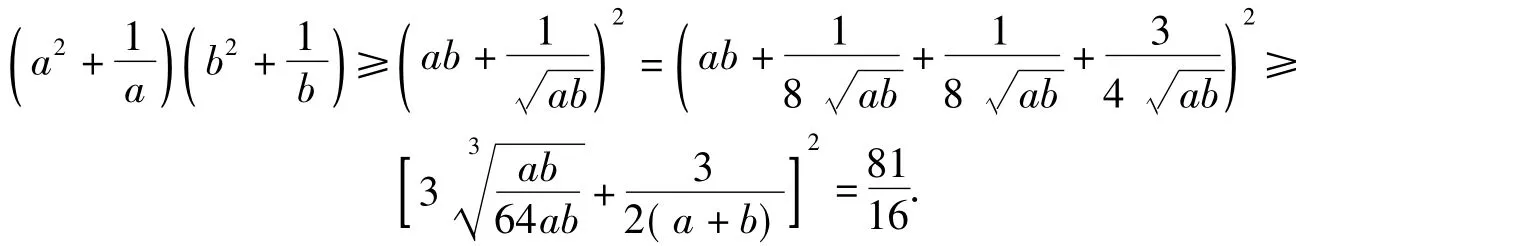
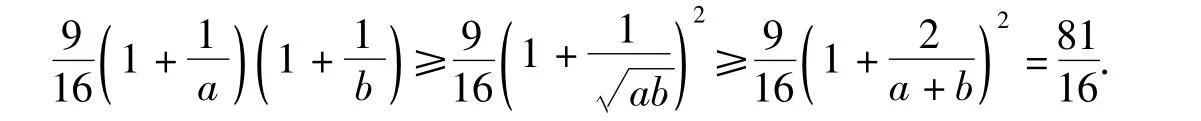
评注上述过程中使用均值不等式时的配凑，对多数学生而言，都可在明确的目标启导下完成．再看从局部入手的方法:

思路4由题意及柯西不等式知

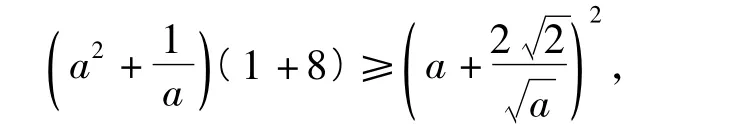
从而

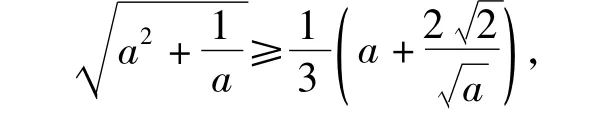
同理可得

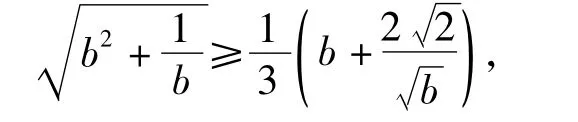
故

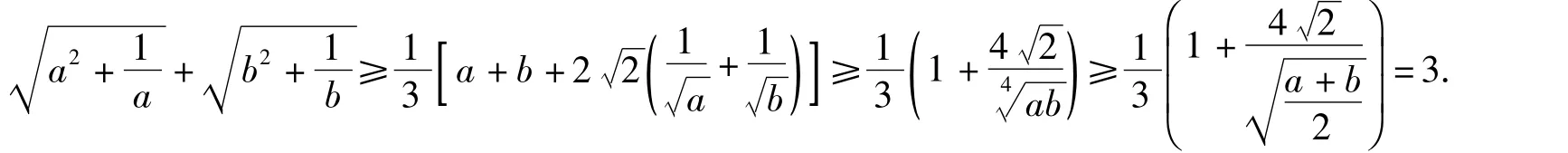
一道好题的平淡之中见深刻的命题之意和考查目的，根植于基础知识和基本方法．而遵循通性通法的解题原则:思想，越自然越好;方法，越简单越好;所用知识，越基础越好．这是实现简单自然解题的重要保证．

参考文献

［1］吴成强．添“0”法的运用［J］．中学数学教学参考:上旬，2015(9):35-36．

作者简介:邵明宪(1957－)，男，河南方城人，中学高级教师，研究方向:数学教育．

修订日期:*收文日期:2015-11-27;2015-12-30．

中图分类号:O12

文献标识码:A

文章编号:1003－6407(2016)04-封三-02