从自然走向更自然*

●李玉荣　(金陵中学河西分校　江苏南京　210019)



从自然走向更自然*

●李玉荣(金陵中学河西分校江苏南京210019)

摘要:在课堂上让学生求解一道“网络征解”题，多种途径作垂线构造直角三角形利用勾股定理求解，但在解所列方程时遭遇困难，引导学生转变思维，实现解题方法从自然走向更自然，并精选配套问题让学生练习，促使学生深化知识、形成能力．

关键词:构造;直角三角形;方程;相似三角形;模型

学数学离不开解题，解题教学是教师永无止境的话题，正如著名数学教育家波利亚所说:中学数学教学的首要任务就是加强解题训练．这里的训练应是师生共同的任务．近日，笔者从网上偶遇一道征解题，感觉有一定的思维力度，经过自己的求解后让学生探究解法，在与学生的对话交流中，体验了解法从自然走向更自然的蜕变，在此与大家分享．

活动1出示题目后，教师给学生一定的时间独立思考，然后小组交流解法、解题感受及受阻原因．

生1:题设中∠B=45°为特殊角，一般应联想到直角三角形，可考虑过点A作BC的垂线，题目中的未知线段较多，解题通法是设未知数、构造方程求解．

如图1，作AH⊥BC于点H，则

设AD=AE=x，则

由AH·DC=AD·AC得

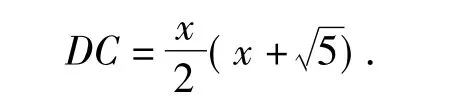
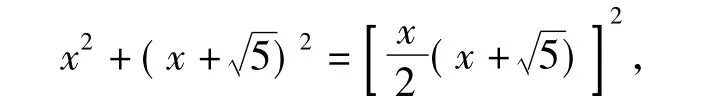
在Rt△ADC中，但在解方程时却遭遇了困境．

生2:注意到题设中∠B=45°为特殊角，于是考虑过点A作BA的垂线构造直角三角形，再设未知数，列方程求解．

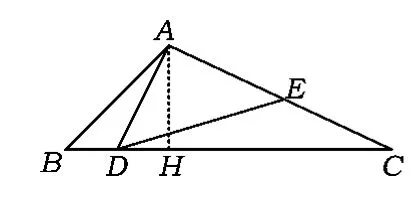
图1

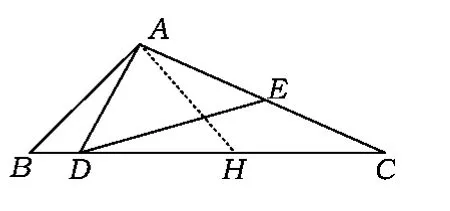
图2

如图2，作AH⊥BA交BC于点H，则

设AD=AE=x，则

由∠DEC=∠AHC=135°，∠C=∠C，可得△DEC∽△AHC，从而

在Rt△ADC中，

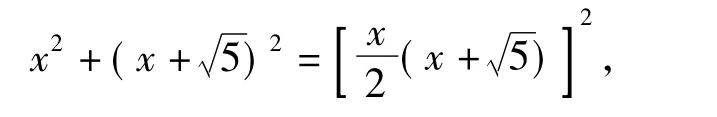
在解方程时也遭遇了同样的困境．

生3:我们也是构造直角三角形列方程求解的．

如图3，过点E作EH⊥AC交BC于点H，设AD=AE=x，则

易证△DEH∽△ABD，从而

即

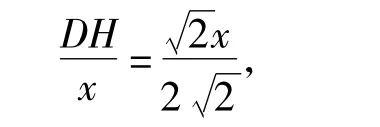
可得

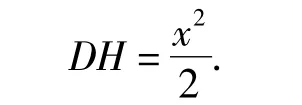
因为AD∥EH，所以

即

可得

从而

在Rt△ADC中，

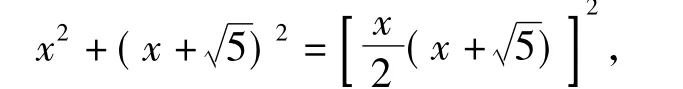
在解方程时也遭遇了同样的困境．

图3

图4

生4:我们也是构造直角三角形列方程求解的．

如图4，过点C作CH⊥AC交DE的延长线于点H，则

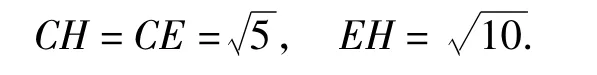
设AD=AE=x，则

易证△DCH∽△ABD，从而

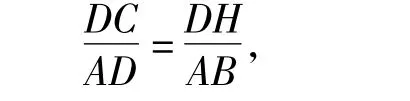
即

可得

在Rt△ADC中，

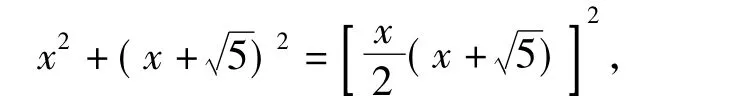
在解方程时也遭遇了同样的困境．

生5:我们也是构造直角三角形列方程求解的．

如图5，过点D作DF⊥DE交CA的延长线于点F，则DF=DE，且∠F=∠AED=45°=∠B．又∠FCD=∠BCA，从而△FCD∽△BAC，可得

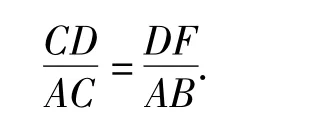
设AD=AE=x，则

从而

可得

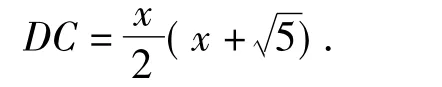
在Rt△ADC中，

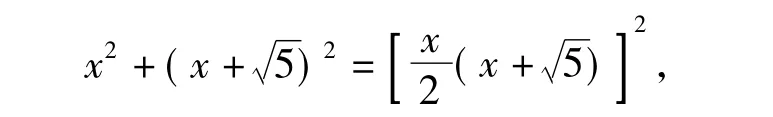
在解方程时也遭遇了同样的困境．

图5

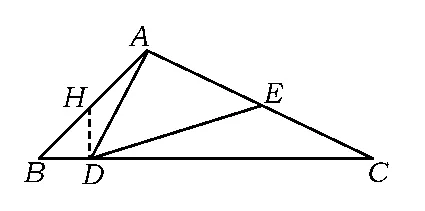
图6

生6:我们和前面几位同学的思路相同，也是构造直角三角形列方程求解的．

如图6，过点D作DH⊥BC交AB于点H，设AD=AE=x，BD=DH=a，则

易证△DAH∽△CDE，从而

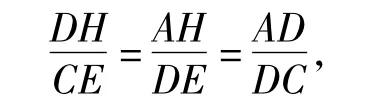
即

可得

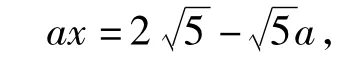
即

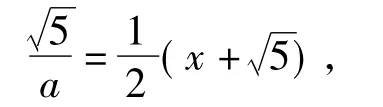
故

在Rt△ADC中，

在解方程时也遭遇了同样的困境．

师:6位同学从不同角度构造直角三角形、列方程求解，这是解决这类问题的通法，非常自然．但他们得到的方程是一元四次方程，在如何解这个方程方面遇到了困难，怎么处理?

同学们可能最先想到将原方程整理得

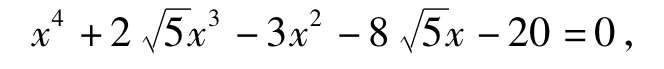
尝试得

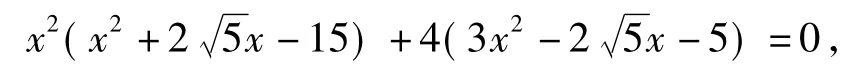
因为x＞0，所以

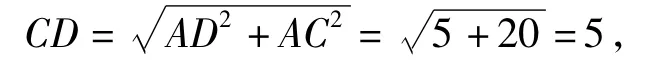
显然，这里的因式分解学生是难以完成的．可不可以换个角度思考?

原方程可化为

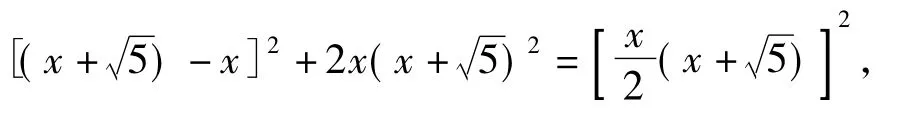
解得t=10(负根舍去)，从而

虽然问题最终得解(教师之前做足了功课)，但美中不足的是这几种看似自然的解法在解方程时却显得不够自然，学生无法顺利求解．

(没有学生提出其他解法，教师继续给予启发．)

师:对于等腰Rt△ADE，有∠ADE=45°，于是∠B=∠ADE=45°，这是一个很重要的数量特征，能否联想到一个重要的基本图形来求解?

活动意图立足解题通法，在已有思考的基础上总结解题不成功的原因，从图形的数量关系特征过渡到图形的形状特征，从自然走向更自然．

活动2学生继续思考，教师巡视，大约5分钟后有学生举手．

生7:如图7，分别延长AB，ED交于点H，易证△CDE∽△HDB∽△HAD，从而

可得

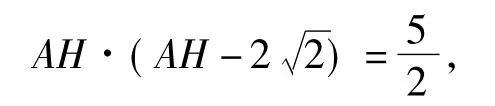
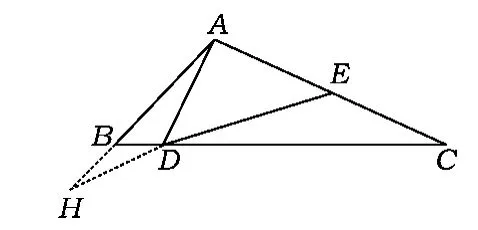
图7

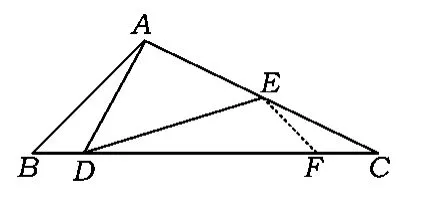
图8

生8:如图8，在DC上取点F使∠DFE=45°，产生“一线三等角模型”，得到△ABD∽△DFE，从而

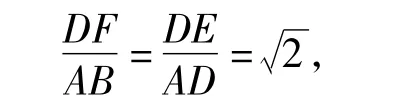
于是

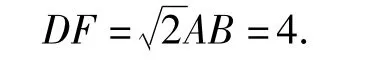
因为∠AED=∠C+∠EDC=45°，∠EFC=∠C+ ∠FEC=45°，所以

又因为∠C=∠C，所以

从而

即

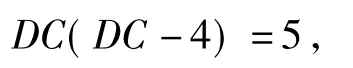
解得DC=5(负根舍去)．

师:生7、生8能顺利解决问题的关键是什么?

生9:生7利用∠EDC=∠BAD巧妙地构造了3对相似三角形;生8利用条件构造了“一线三等角模型”得到2对相似三角形，他们都避开了前面涉及的一元四次方程．

活动意图注重知识关联，避免解题中形成思维定势．《数学课程标准(2011版)》提出了模型思想．应用模型思想寻求解题思路，可以排除其他因素的干扰，提高思维的敏捷性．有许多重要的数学模型，需要教师引导学生去发现、归纳、提炼，再研究它们的应用．

活动3精选2道中考题，学生独立解答，归纳解题中运用的思想方法．

练习1如图9，在四边形ABCD中，AD=4，CD=3，∠ABC=∠ACB=∠ADC=45°，则BD的长为______．

(2014年湖北省武汉市数学中考试题)

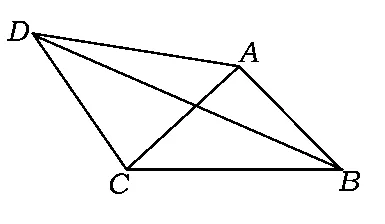
图9

图10

解如图10，过点C作CE⊥AD交AD于点E，过点B作BF⊥AD交DA的延长线于点F．因为∠ADC=45°，所以

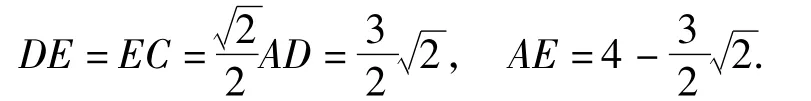
又因为∠ABC=∠ACB=45°，所以△ABC为等腰直角三角形，从而△EAC≌△FBA，得

于是

因此在Rt△BFD中，

(2015年江西省南昌市数学中考试题)

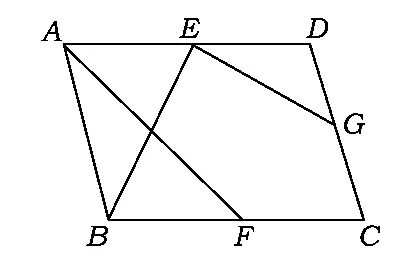
图11

图12

解如图12，作AH⊥BC，BM⊥AD，GN⊥AD，垂足分别为H，M，N，则AH=BM，HB=AM，易证△BMA∽△GND，△BME∽△ENG，从而

设DN=x，GN=y，则

从而

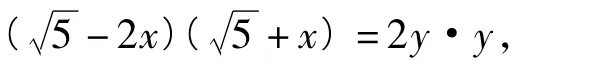
即

在Rt△DGN中，

把式(2)代入式(1)，得

在Rt△AFH中，

活动意图作垂线构造直角三角形或构造“一线三等角模型”解题是本节课研究的重点．学生仅仅靠听一道例题是难以真正掌握解法的，通过2道配套练习的求解，引导学生对学习结果主动反思，从“会”到“通”，促使学生深化知识、形成能力．

罗增儒教授提到“学会解题的4步骤程式”，即简单模仿、变式练习、自发领悟、自觉分析．“自发领悟、自觉分析”很大程度上要求解题者能有解题的自我控制能力，有反思能力，如果学生每解决一个问题都能如此思考，关注数学方法，提炼数学思想，领悟解题策略，挖掘数学本质，提升学习潜能，解题思维品质将会不断提高，从自然最终走向更自然．

作者简介:李玉荣(1963－)，男，江苏句容人，中学高级教师，研究方向:初中数学教学、解题与命题研究．

修订日期:*收文日期:2015-11-27;2015-12-30．

中图分类号:O124．1

文献标识码:A

文章编号:1003－6407(2016)04-42-04