从一堂教改实践课谈学生数学思维的培养*

●洪　琼　(天台中学　浙江天台　317200)



从一堂教改实践课谈学生数学思维的培养*

●洪琼(天台中学浙江天台317200)

摘要:数学教学的主要目的是发展学生的数学思维能力．课堂教学的有效性体现在对教学内容的把握和课堂氛围的营造上．发现学生的思维关节点、恰当的策略指导和优化解题教学是有效发展学生数学思维的几个关键点．

关键词:数学思维;思维关节点;策略指导;解题教学

笔者参加浙江省高中数学名师培养工程第2次活动时，在金华市外国语学校观摩了一堂教改实践课“导数在构造函数中的应用”．进入听课教室，笔者就发现课桌不是传统的一人一桌，学生座位的安排也不是传统的“秧田”式整齐排列，而是5个人为一个学习小组围坐在长方形大桌子旁，学生抬头可以直面黑板．笔者针对听课内容谈自己的一些体会，供大家参考．

1　案例回顾

1．1课前准备

教师印发学生导学案，学案内容包含学习目标和3个例题．课前，教师要求学生初步完成学案．

学习目标:理解函数的零点、方程的根、2个函数图像交点这3者之间的关系;熟练运用导数分析图像的单调性、曲线相切问题等;理解函数构造中的常见策略，学会多角度分析问题．

例1已知m∈R，讨论关于x的方程x3－3x－m=0的根的个数(尝试多种方法并进行方法小结)．

1．2师生互动

教师针对例1，向学生征集解决方案．

生1:构造函数f(x)=x3－3x－m，研究函数f(x)的零点(记为方法1)．

(学生分析思路，教师按学生思路板书．当学生通过求导确定函数的单调区间后，教师画出函数的简图．学生对含参数m的极大值、极小值与0的关系进行讨论，得出答案．)

师:把方程的根转化为函数的零点．

生2:转化成x3－3x=m，研究函数f(x)=x3－3x和函数y=m的交点个数(记为方法2)．

师:为什么要把m移到等式右侧?比起第1种方法有优势吗?

生2:生1构造的一元三次函数含有m，函数不确定，需要对函数进行讨论．把m分离之后，等式左侧的函数是确定的一元三次函数．而y=m的图像是平行于x轴的直线，比较容易观察．

师:第1种方法和第2种方法有什么共同点?

生2:都是研究一元三次函数的图像和直线的交点．

师:没错，都是把方程的根转化为2个函数图像的交点．在第1种方法中，函数零点可以理解为函数y=f(x)与函数y=0图像的交点．

生3:方程可转化为x3=3x+m，研究函数f(x)=x3和函数g(x)=3x+m的交点个数，只需找出直线与一元三次函数图像相切的情况即可(记为方法3)．

(学生上台板演，写出解题过程．学生讲解比较快，思维跳跃性强，因此教师通过几何画板演示函数g(x)=3x+m当m变化时图像变化过程，弥补学生讲解时的不完整．该方法讲完后，整个教室陷入了静寂．)

师:前面3种方法都是转化为一元三次函数的图像问题，有没有其他方法?能不能转化成其他熟悉的初等函数形式?

(教师提醒学生要注意当x=0时的讨论．学生上台板演，对m进行讨论，画出简图(如图1所示)，但是在研究二次函数曲线和反比例函数图像曲线相切的时候遇到了困难．教师协助其求出2条曲线相切时m的值．)

师:当m＞0时，设2条曲线相切的公共切点为M(x0，y0)，则2条曲线在该切点处的切线斜率相等．易知f'(x)=2x，，由

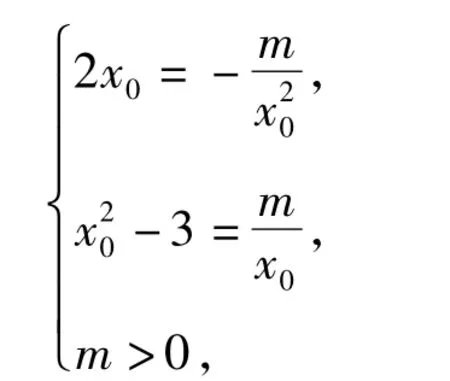
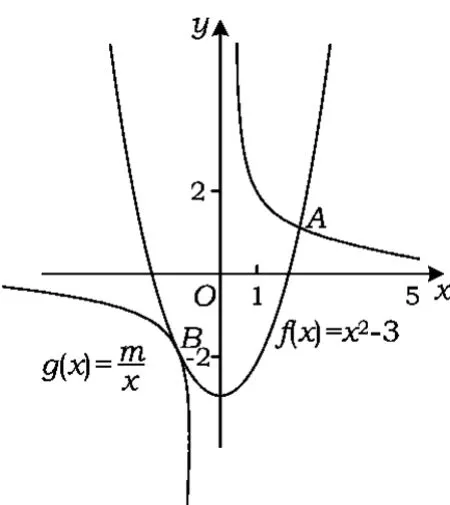
图1

解得x0=－1，m=2．

当m＜0时，同理可解得x0=1，m=－2．

当m变化时，用几何画板演示图像变化情况．

师(点评):以上解题方法都是通过将方程转化为不同形式，等式2侧可记作不同函数，研究函数图像的交点个数．等式2侧可配比成各种各样的函数形式，理论上都可行，但是尽量选择我们熟悉的函数形式．

在解决完例1后，教师让学生小组合作讨论例2的解决方案，审视原来的解题方案并进一步完善，以小组为单位展示成果．

1．3生生合作

学生按教师事先分好的学习小组进行讨论，讨论过程中可看见合作小组的学生在相互交换自己的学案、演算和讨论．

1．4学生展示

每个学习小组派一位代表上台用幻灯片展示自己的学案，并进行讲解．

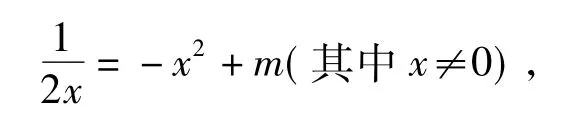
(学生展示详细解答过程，思维清晰，运算准确，语言幽默，其他学生鼓掌表示肯定．)

师:与例1的方法4一致．

小组2:将原方程转化为

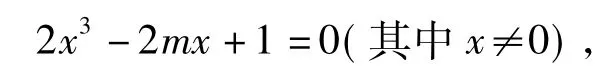
研究函数f(x)=2x3－2mx+1(其中x≠0)与x轴的交点个数．

(学生展示详细解答过程．)

师:考虑问题非常周到，注意到了转化的等价性，即当x≠0时研究函数f(x)的导数，对m的讨论很完整．

(其他学生鼓掌表示肯定．)

小组3:把原方程转化为

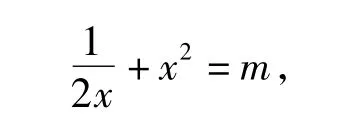
师:为什么要这样转化?f(x)是什么函数，大家熟悉吗?图像是什么形状?

生6(在幻灯片上作图讲解):参数分离后，函数f(x)是确定的函数．可以通过研究函数的导数来研究函数f(x)的简图(如图2所示)．易知

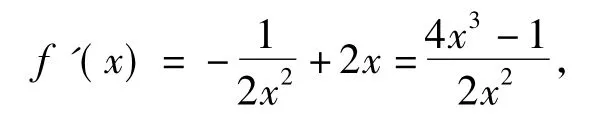
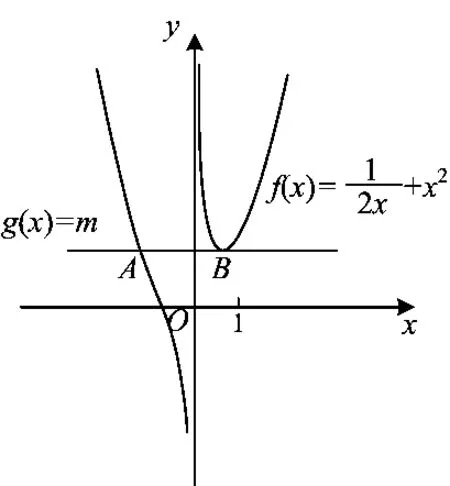
图2

师:对于x≠0这个“断点”的考虑非常细致，运用了极限思想来判断图像的趋势．

小组4(作图板演):将原方程转化为

研究函数f(x)=x3和的交点个数．

2　课堂效果

本节课安排在函数与导数学习之后，设计的例题思维入口宽、切入点多，有利于学生的思维发散和一题多解．课堂中教师是一个真正的组织者，采用的方式就是组织学生小组合作交流．学生是课堂的主人，自主学习、自主探究并充分表达自己的见解．教学的重点是函数与方程思想、转化与化归思想的运用．教师鼓励学生呈现不同的思维过程，学生在表达自己想法的过程中去伪存真、完善自我、开拓思维．学生的思辨能力、表达能力都非常强，落落大方，到讲台板演讲解都十分自然．课堂气氛是宽松愉悦的，尤其是到讲台讲解的几个学生，非常幽默，逗得其他学生大笑．从这些都可以看出，这样的教改实践课不是第一次，而是经过一段时间的积累和锻炼，学生十分适应而且各方面素质都得到了较大的提高．

3　关于教改实践课的几点思考

美国教育大师杜威曾说过“学习就是要学会思维”、“教育在理智方面的任务是形成清醒的、细心的、透彻的思维习惯”．数学是思维的科学，因此数学教学更应该在发展学生思维上承担更大的责任．因此，从宏观上说，数学教学的目的是发展学生思维，优化数学品质，培养数学核心素养．结合案例，笔者谈谈以下4点思考:

3．1创设研究性、开放性、自主性的课堂氛围

目前高中数学课堂教学非常注重效率，尽管课堂教学中学生的主体性有所加强，但总体来说仍然是灌输式的．教师对课堂充分预设，内容满满当当，学生缺乏学习兴趣，学得累．只有富有研究性、开放性、自主性的课堂教学才能更好地促进学生在情感、态度、习惯、思维能力等方面更好地发展．只有通过加强学生自身对学习的体验，使学生从大量繁杂、重复的技能训练中解放出来，才能让学生有更多精力投入到探索性的数学活动中去，才能更好地促进思维发展、技能运用［1］．笔者在课后与上课师生交流，他们对这种上课方式习以为常．在谈及教学内容完成的量时，教师提到设计例题时就已经考虑到有可能来不及，因为无法预料学生的想法以及学生表达的时间．在考虑“例题的量”与“学生表达的质”的选择时，毫无疑问要选后者．因为学生表达的过程就是思维展现的过程，也是自我修正的过程．在教改实践课中，我们应该把创设开放性的问题和引导学生清晰表达自己的思维过程作为课堂教学的目标之一．

3．2寻找和利用思维的关节点

人的身体有许多关节点和穴位，思维也一样．数学教学应该寻找、抓住并利用好思维的关节点．教师如果不知思维的关节点所在，平均用力，眉毛胡子一把抓，那么学生只能停留在机械模仿的水平上［1］．这种教学的有效性取决于教师的功力．在本堂课中，教师在多个地方设置了精巧的问题，打通了学生的思维关节点．例如，在例1中提出2个问题:方法2与方法1相比有什么优势?2种方法的共同点在哪里?不仅让学生悟出问题的本质都是通过转化变成一元三次函数和直线的交点问题，也让学生明白参数分离的作用是让一元三次函数成为确定的函数．但遗憾的是，在方法3中，教师没有抓住思维的关节点，方法3的本质也是一元三次函数与直线的交点问题，但是最重要的区别是方法1和方法2中的直线都是平行于x轴，直线相切时的切点在极值处．而方法3需要求切点不明确情况下曲线的切线．如果教师能在方法3结束后设置几个问题突出思维关节点，效果会更好．另外，在小组3呈现的例2的解决方法中，学生构造的x2并不是我们所熟悉的初等函数模型，利用导数来研究陌生函数的图像也是一个思维关节点所在，教师对于“断点”的点评非常到位，能有效优化和促进学生思维的发展．当然，教师在与学生对话的过程中，缺乏一些正中要害的问题，比如“为什么要选择这样的转化方式?你尝试过其他方式吗?”这才是思维的“穴位”所在．通过提问的方式促进学生思考比教师直接点评总结效果会更好．

3．3加强策略指导

教师的核心职责是保障学生的学习权，提升学生以思维力为核心的自主学习力．教师要基于学生现有思维水平与学习习惯，通过思维策略指导，有效突破思维的难点和障碍，使得探究的问题在学生的最近发展区内．在例1的综合点评中，提到方程转化的最终目的是构造等式2侧不同的函数形式，在构造过程中要尽量寻找熟悉的初等函数模型．这是整堂课的思维关键点所在，也是解决这类问题的基本策略．例1的方法4中，学生研究二次函数曲线和反比例函数图像曲线相切的时候遇到困难，教师就直接给出解答方法．很遗憾教师没有把握住这个思维的关节点．学生思维的障碍点在于2条曲线相切问题．教师完全可以引导学生将2条曲线相切理解成2条曲线同时相切于某1条直线并有公共的切点，转化成学生最近发展区内的直线与曲线相切问题．

3．4优化解题教学

学数学离不开训练，离不开解题，但训练的目的和侧重点是解题的技能技巧还是解决问题的思维方法，这是一个重大的原则性问题．重在训练技能技巧可能会禁锢学生的思维，而重在思维训练可以促进思维更好地发展．这堂课在教学内容的选择和教学方法上都是围绕着促进学生思维的发展．一题多解的例题让学生的思维更有变通性．利用一题多解可以构建新知识的最近发展区，寻找知识的生长点，激发学生探究问题，不断从一类问题转化为另一类问题，让学生在探究中感悟转化与化归思想的妙处，建构知识网络．而这堂课的精彩之处就在于所有的问题解答都来自于学生的表达，完整展现了学生思维的特点和缺陷．遗憾之处就在于例2学生所呈现的方法都是例1方法的类比，没有学生尝试其他方法．

数学教学要时刻关注学生的思维过程，教师要准确把握知识与例题所蕴含的数学思想方法和思维方法，准确把握学生的思维起点与难点，设置合理的问题和巧妙的点拨，才能有效发展学生思维．

参考文献

［1］李昌官．寻找数学内在的力量［M］．宁波:宁波出版社，2014．

作者简介:洪琼(1982－)，女，浙江台州人，中学高级教师，研究方向:数学教育．

修订日期:*收文日期:2015-11-03;2015-11-16．

中图分类号:O12

文献标识码:A

文章编号:1003－6407(2016)04-21-04