例谈方程整数解问题的解法

●

(新星学校 浙江苍南 325800)

例谈方程整数解问题的解法

●易永彪

(新星学校 浙江苍南 325800)

在各类数学竞赛和高中自主招生考试中,二次方程整数解问题备受关注.它将古老的整数理论与传统的初中数学知识相结合,涉及知识面宽、范围广,往往需要灵活地运用相关概念、性质、方法和技巧,综合性强,对学生的能力有较高的要求.本文将对方程整数解问题的解法与基本策略作一探索,旨在抛砖引玉.

1 巧用因式分解

例1方程-m4+4m2+2nm2+2n+5=0的正整数解有

( )

A．1组 B．2组 C．4组 D．无穷多组

(2009年浙江省温州中学自主招生考试试题)

解原方程可化为

m4-(2n+4)m2-(2n+5)=0,

可得

[m2-(2n+5)](m2+1)=0.

因为

m2+1gt;0,

所以

m2=2n+5.

(1)

因此m为奇数,不妨设m=2k+1(k为自然数),代入式(1)得

k2+k-1=2n-2.

因为k2与k的奇偶性相同,所以k2+k-1是奇数,不能被偶数整除,因此2n-2只能为1，从而

n=2,m=3,

原方程只有1组正整数解.故选A.

例2已知方程a2x2-(3a2-8a)x+2a2-13a+15=0(a≠0)至少有一个整数根,求整数a的值.

解已知方程经整理得

[ax-(a-5)][ax-(2a-3)]=0,

解得

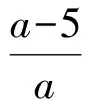
由题意知a为整数,因此a的取值为

1,3,5,-1,-3,-5.

评注分析方程的形式特征,可采用因式分解、求根公式等方法求得方程的根,再结合整除性质、奇偶性等进行求解.

2 巧用判别式

例3设m为整数，且4lt;mlt;40，方程x2-2(2m-3)x+4m2-14m+8=0有2个相异整数根，求m的值及方程的根．

解由题意知

Δ=4(2m-3)2-4(4m2-14m+8) =4(2m+1).

对4lt;mlt;40的整数m，要使Δ=4(2m+1)为完全平方数的m只能取为12和24，而

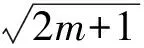
因此当m=12时，x1=16,x2=26；当m=24时，x1=38,x2=52.

例4已知p为质数,使二次方程x2-2px+p2-5p-1=0的2个根都是整数,求出p的所有可能值.

解由已知整系数二次方程有整数根,得

Δ=4p2-4(p2-5p-1)=4(5p+1)

为完全平方数,从而5p+1为完全平方数.因此可设5p+1=k2.注意到p≥2,因此k≥4,且k为整数，于是

那么k+1与k-1中至少有一个是5的倍数,即k=5a±1(a为正整数),因此

5p+1=(5a±1)2=25a2±10a+1,

解得

p=a(5a±2).

由p为质数,5a±2gt;1,可知a=1,因此

p=3或p=7.

当p=3时,原方程变成x2-6x-7=0,解得

x1=-1,x2=7；

当p=7时,原方程变成x2-14x+13=0,解得

x1=1,x2=13.

故p=3或p=7.

评注因为整系数二次方程有整数根,所以Δ必为完全平方数．当问题比较复杂时，可通过恰当设元、引入参数,利用因式分解、数论等方法求解．

3 巧用韦达定理

例5求使关于x的方程kx2+(k+1)x+k-1=0的根都是整数的k值.

解当k=0时,x=1符合题意.

当k≠0时,设方程kx2+(k+1)x+k-1=0的2个根为x1,x2(x1≤x2),因此

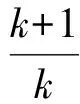
(2)

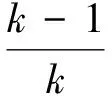
由式(2)-式(3)得

x1+x2-x1x2=-2,

于是

(x1-1)(x2-1)=3,

解得

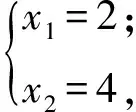
从而

综上所述,满足题意的k值为

例6已知关于x的一元二次方程x2+cx+a=0的2个整数根恰好比方程x2+ax-b=0的2个根都大1,求a+b+c的值.

(2011年全国初中数学竞赛试题)

解设方程x2+ax+b=0的2个根为α,β,其中α,β为整数,且α≤β,则方程x2+cx+a=0的2个根为α+1,β+1.由题意得

α+β=-a,(α+1)(β+1)=a,

两式相加得

αβ+2α+2β+1=0,

即

(α+2)(β+2)=3,

解得

又因为

a=-(α+β),b=αβ,c=-[(α+1)+(β+1)],

所以a=0,b=-1,c=-2；或a=8,b=15,c=6,

故

a+b+c=-3或a+b+c=29.

评注从根与系数的关系式中消去参数,可得关于两根的不定方程,借助因数分解、因式分解求解.

4 巧用主元更换

例7若关于x的方程ax2+2(a-3)x+(a-13)=0至少有一个整数根,求非负整数a的值.

ax2+2(a-3)x+(a-13)=0,

化简得

(x+1)2a=6x+13,

因此

即

x2-4x-12≤0,

解得

-2≤x≤6.

因为x为整数,x≠-1,所以x的值可取为

-2,0,1,2,3,4,5,6.

把x分别代入求得a的值,且a为非负整数,可得a的值为1,13.

例8已知

试求x2+y2+z2+u2的值．

解本题为四元二次方程，直接求解相当困难，但各个方程结构完全相同，因此可考虑更换主元．原方程与

等价，这里t的值为4,16,36,64.

当t≠1,9,25,49时,方程(4)与

(t-9)(t-25)(t-59)x2+

(t-1)(t-25)(t-49)y2+

(t-1)(t-9)(t-49)z2+

(t-1)(t-9)(t-25)u2-

(t-1)(t-9)(t-25)(t-49)=0

(5)

等价.而式(5)是关于t的四次方程，至多有4个根.因为t=4,16,36,64是式(4)的根，所以必为式(5)的4个根，即式(5)等价于

(t-4)(t-16)(t-36)(t-64)=0.

对比展开式t3的系数可得

x2+y2+z2+u2+1+9+25+49=

4+16+36+64，

故

z2+y2+z2+u2=36．

评注当一个方程按常规意义下的求解比较困难时,可以通过观察方程的结构特征，选择更换主元，使方程次数和结构形式发生变化，从而转化为一个容易求解的问题．