函数的妙用
2011-11-21
●
(绍兴县实验中学 浙江绍兴 312030)
函数的妙用
●毛幼娥
(绍兴县实验中学 浙江绍兴 312030)
函数的实质是表述运动与变化过程中的变量间的动态关系.培养学生运动与变化的观念,是中学数学教学的重要目标之一.本文结合实例对与之有关的问题作一些剖析,以便能从中领略此类问题的一些处理方式和解决策略.
1 构造函数证明不等式
根据式子的特点,构造适当的函数,以利用其性质解题.
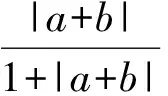
分析本例不等式的左边与右边有明显的共同特征,据此可构造一个新函数,运用此函数的递增性给出证明.
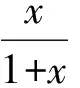
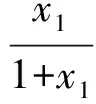
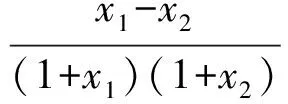
因此f(x)在[0,+∞)上是增函数,而
0lt;|a+b|≤|a|+|b|,
于是
f(|a+b|)≤f(|a|+|b|),
即
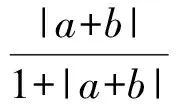
例2设x,y,z∈(0,1),求证:
x(1-y)+y(1-z)+z(1-x)lt;1.
分析此题中的变量x,y,z有轮换对称性,可考虑构造其中一个变量的函数,利用一次函数的单调性给出证明.
证明设f(x)=(1-y-z)x+y+z-zy-1(0lt;xlt;1),把y,z看作常数,则f(x)是关于x的一次函数.因为
f(0)=y+z-yz-1=-(y-1)(z-1)lt;0,
f(1)=(1-y-z)+y+z-yz-1=-yzlt;0,
所以对于0lt;xlt;1,都有f(x)lt;0,即
(1-y-z)x+y+z-zy-1lt;0,
故
x(1-y)+y(1-z)+z(1-x)lt;1.
例3a,b,c是三角形的3条边长,求证:
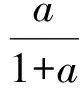
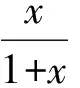
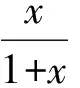
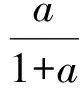
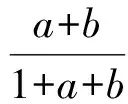
2 妙用函数图像解方程
华罗庚先生曾说过“数缺形时少直观,形少数时难入微”.把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”或“以数解形”,可以使复杂问题简单化、抽象问题具体化,从而达到优化解题的目的.
例4设方程-x2+4x-3-m=0在0≤xlt;3上有唯一解,求实数m的取值范围.
分析方程左边是二次函数,它在区间上有唯一解.这些特征适宜借助函数图像,利用数形结合解题.
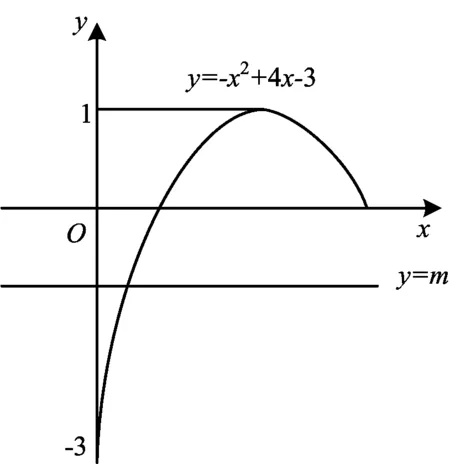
图1
解考虑函数y=-x2+4x-3和y=m,并在同一坐标系内作出这2个函数的图像(如图1).y=m的图像是与y轴垂直的直线,可以上下平行移动.在移动过程中,当它和抛物线弧段y=-x2+4x-3(0≤xlt;3)只有一个交点时,m需满足
-3≤m≤0或m=1.
故m的取值范围是-3≤m≤0或m≤1.
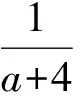
分析学生最容易犯错的解法是将已知条件转化为a+4lt;5-3a,因为此时不是单调性问题了.若用通常的不等式解法,则不仅繁琐,而且不易考虑周全;若能借助图像,则过程就清晰多了.
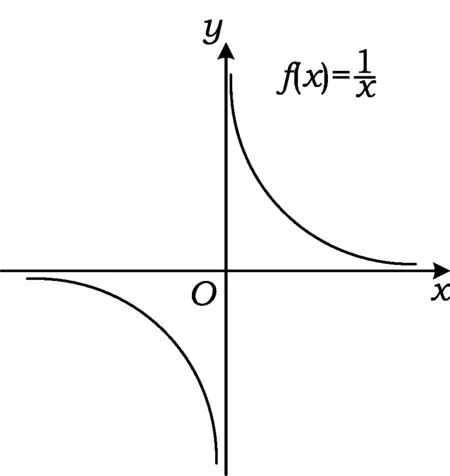
图2
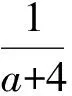
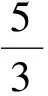
a+4gt;0,5-3agt;0.
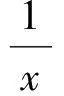
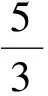
a+4lt;0或5-3alt;0,
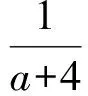
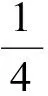
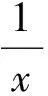
( )
A.3个 B.2个 C.1个 D.0个
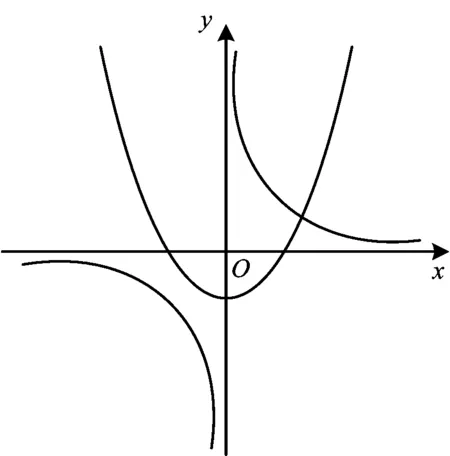
图3
分析如果采用去分母的方法转化为整式方程来解,那么又化为解一个三次方程了;但若采用等价转化为函数,则利用函数图像就容易解决了.
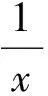
3 应用函数建模解决实际问题
一次函数、二次函数与现实生活联系紧密,函数应用题可考查学生的建模能力.具体解题过程则仍可用如下的图解方法:
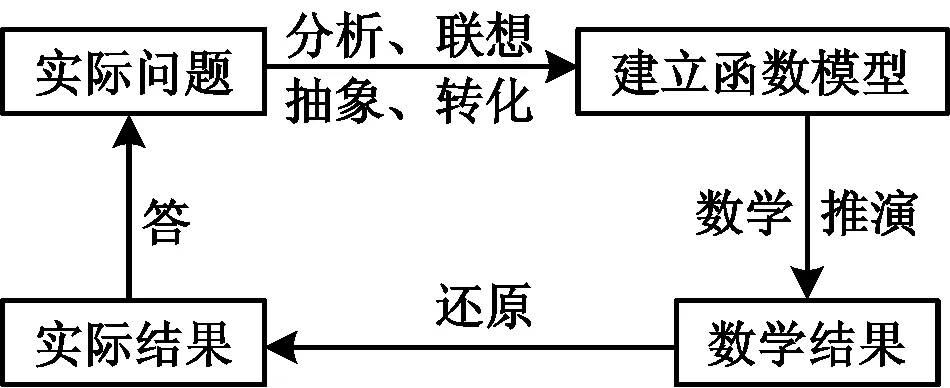
例7某种商品在近30天内,每件的销售价格P(元)与时间t(天)(t∈N)的函数关系近似地满足:
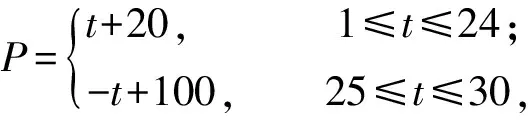
商品的日销售量Q(件)与时间t(天)的函数关系近似地满足:Q=40-t(1≤t≤30).求这种商品日销售金额R的最大值,并指出销售金额最大的一天是30天中的第几天.
分析日销售金额=日销售价格×日销售量,因此先把日销售额与时间的函数关系写出来,然后根据函数解析式求日销售金额R的最大值,同时求出销售金额最大的一天是30天中的第几天.
解由题意得
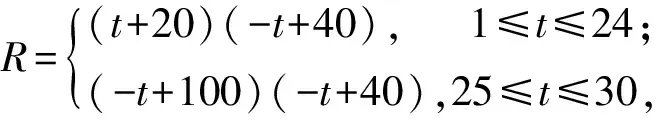
即
因此当1≤t≤24时,取t=10,最大销售金额为900元;当25≤t≤30时,取t=25,最大销售金额为1 125元.故这种商品日销售金额R的最大值为1 125元,销售金额最大的一天是30天中的第25天.
例8某化工集团在靠近某河流区修建2个化工厂,流经第一化工厂的河流流量为500万立方米/天,在2个化工厂之间还有一条流量为200万立方米/天的支流并入大河(如图4).第一化工厂每天排放含有某种有害物质的工业废水2万立方米;第二化工厂每天排放这种工业废水1.4万立方米,从第一化工厂排出的工业废水在流到第二化工厂之前,有20%可自然净化.环保要求:河流中工业废水的含量应不大于0.2%,因此,这2个工厂都需各自处理部分的工业废水.第一化工厂处理工业废水的成本是1 000元/万立方米;第二化工厂处理工业废水的成本是800元/万立方米.试问:在满足环保要求的条件下,2个化工厂应各自处理多少工业废水,才能使这2个工厂总的工业废水处理费用最小?
分析可先根据已知条件建立函数模型.
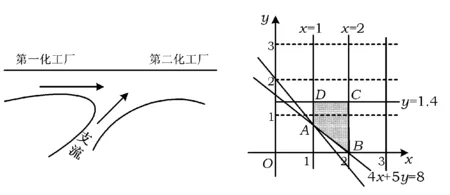
图4 图5
解设第一化工厂每天处理工业废水x万立方米,需满足
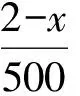
设第二化工厂每天处理工业废水y万立方米,需满足
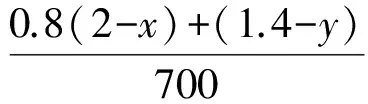
因此2个化工厂每天处理工业废水总的费用为z=1 000x+800y元,于是原问题即可转化为:在约束条件下,求目标函数z=200(5x+4y)的最小值.
借助于建立函数关系式或构造中间函数,再结合函数的图像与性质,能解决许多有关最值、解(证)不等式、解方程等方面的问题.函数与方程、不等式的结合体现了函数图像与方程、不等式的内在联系;体现了特殊与一般的辨证联系.
