角元塞瓦定理的应用

●

(天津师范大学数学教育科学与数学奥林匹克研究所 天津 300387)

角元塞瓦定理的应用

●李建泉

(天津师范大学数学教育科学与数学奥林匹克研究所 天津 300387)

在数学学习中，平面几何是训练学生思维能力的重要环节.竞赛中与此相关的知识对于参加自主招生考试的学生来说帮助很大.下面通过塞瓦定理及相关的一些例子加以说明.

塞瓦定理P是△ABC所在平面上的一点，直线PA,PB,PC与直线BC,CA,AB分别交于点D,E,F，则

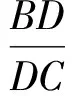
塞瓦定理还有一个三角形式的表述.

角元塞瓦定理P是△ABC所在平面上的一点，直线PA,PB,PC与直线BC,CA,AB分别交于点D,E,F，则

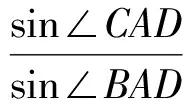
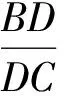
角元塞瓦定理的逆定理若点D，E，F分别是直线BC，CA，AB上的点，且满足

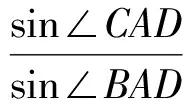
则AD，BE，CF三线交于一点.

下面只给出当点P在△ABC内时塞瓦定理的证明，其他情形的证明类似.

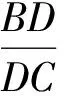
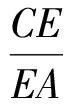
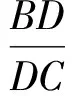
在△PAB中，由正弦定理可得

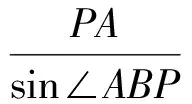
即

PA·sin∠BAD=PB·sin∠ABE.

同理可得

PB·sin∠CBE=PC·sin∠BCF;

PC·sin∠ACF=PA·sin∠CAD.

将这3个等式相乘，可得

sin∠BAD· sin∠CBE·sin∠ACF=

sin∠ABE·sin∠BCF·sin∠CAD，

即

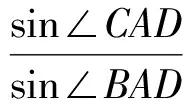
下面给出几个应用角元塞瓦定理的例子.

例1已知O为△ABC内一点，且满足

∠BAO=∠CAO=∠CBO=∠ACO，

求证：△ABC的3条边长成等比数列.

(2011年北京大学保送生考试试题)

分析条件中明显有AO，BO，CO三线交于一点O的条件，但没有给出这3条线与对边的交点，且还给出了与角度有关的条件，应用角元塞瓦定理，再结合分析的方法，可以作为一条寻求解决问题的途径.

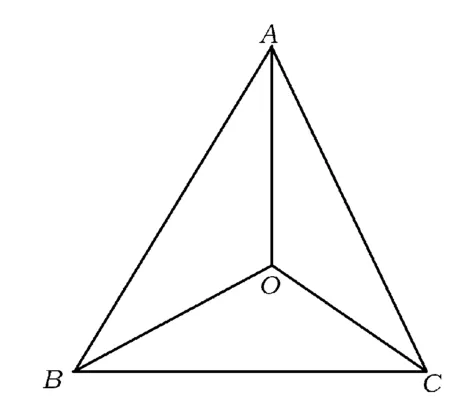
图1

证明如图1所示，设∠BAO=∠CAO=∠CBO=∠ACO=α,∠ABO=β，∠BCO=γ，则4α+β+γ=π.由角元赛瓦定理可得

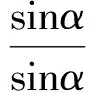
即

sin2α=sinβsinγ.

下面证明BC2=AB·AC.因为

BC2=AB·AC

⟺ sin22α=sin(α+β)sin(α+γ)

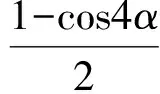
⟺ 1+cos(β+γ)=cos(β-γ)+cos2α

⟺ 1+cosβcosγ-sinβsinγ=cosβcosγ+sinβsinγ+

1-2sin2α

⟺ sin2α=sinβsinγ.

注三角形内满足∠BAO=∠CBO=∠ACO的点O,称为△ABC的布洛卡点.

例2P为锐角△ABC内一点，直线la和PA关于∠A的角平分线对称，直线lb和PB关于∠B的角平分线对称，直线lc和PC关于∠C的角平分线对称.

(1)证明:la,lb,lc三线交于一点Q；

(2)若点P在3条边BC，CA，AB上的投影分别为D，E，F，证明:点P为△DEF的重心的充要条件是Q为△ABC的重心.

分析在第(1)小题中，条件给出的是AP，BP，CP三线交于一点P，仍然没有给出这3条直线与对边的交点，但是给出的对称的条件与角度有关.应该利用角元塞瓦定理将条件转化为等式，结合角元塞瓦定理的逆定理，将要证明的la,lb,lc三线交于一点也转化为证明一个等式，从而使条件与结论联系起来.在第(2)小题中，多个侧面的问题往往可以通过一个侧面突破，从而全面解决问题.

需要说明的是，通过AP,BP,CP的延长线与对边的交点也可以证明这个结论.实际上,很多结论都是等价的，证法也很多，这里只是通过条件和结论之间的关系来寻求一条解决问题的途径.

证明(1)设∠PAB=α，∠PBC=β，∠PCA=γ,la,lb,lc分别与BC,CA,AB交于点L,M,N，则

∠LAC=α,∠MBA=β，∠NCB=γ.

因为PA，PB，PC三线交于一点，所以由角元塞瓦定理得

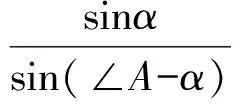
由角元塞瓦定理的逆定理，得la,lb,lc三线交于一点Q.

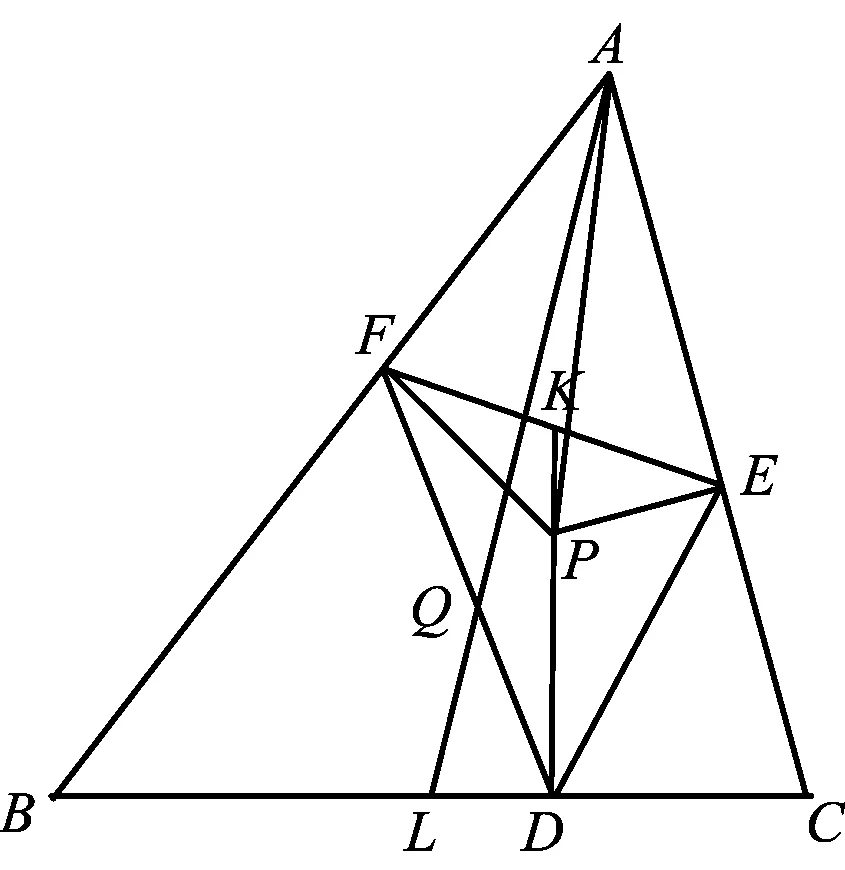
图2

(2)如图2,因为A,E,P,F四点共圆，所以∠PEF=α,∠PFE=∠A-α.设直线DP与EF交于点K，由B，D，P，F和C，D，P，E四点共圆，可得∠FPK=∠B,∠EPK=∠C.在△PFK和△PEK中,由正弦定理可得

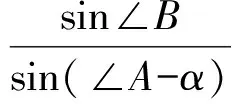
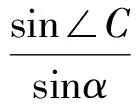
在△ABL和△ACL中,由正弦定理可得

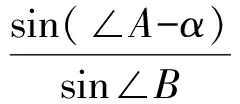
于是

FK=EK,

即

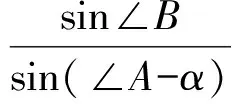
从而

BL=CL.

同理可得,直线EP平分DF的充要条件是CM=AM，直线FP平分DE的充要条件是AN=BN，即点P为△DEF的重心的充要条件是Q为△ABC的重心.

注直线AP,la称为∠A的等角线，P,Q称为△ABC的等角共轭点.

例3已知△ABC的内切圆⊙I分别与3条边BC,CA,AB切于点A1,B1,C1，l为过点I的任意一条直线，A′,B′,C′分别是A1,B1,C1关于直线l的对称点，证明:AA′,BB′,CC′三线交于一点[1].

(2009年保加利亚数学奥林匹克竞赛试题)

分析对称的条件中既有角相等，也有边相等，由对称轴过⊙I的圆心以及弧相等，结合切线的条件，可以得到一些非对称的角度的相等.相似和全等是处理线段和角度关系常用的手段，但是如果在寻求解题途径中无法找到相似和全等，那么常用的方法是运用正弦定理.在处理比例式时，利用面积有时也能起到同样的作用.

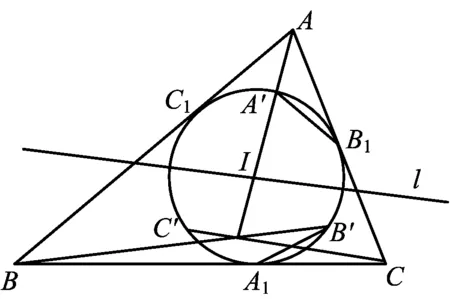
图3

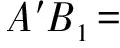
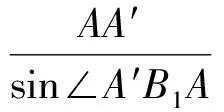
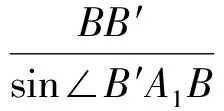
因为

且

所以

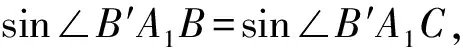
BB′sin∠A1BB′，

即

AA′sin∠CAA′=BB′sin∠CBB′.

同理可得

BB′sin∠ABB′=CC′sin∠ACC′,

CC′sin∠BCC′=AA′sin∠BAA′.

将上面3个式子相乘，可得

sin∠CAA′sin∠ABB′sin∠BCC′=

sin∠CBB′sin∠ACC′sin∠BAA′，

即

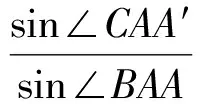
由角元塞瓦定理的逆定理,可得AA′,BB′,CC′三线交于一点.

例4设Γ(I)是以△ABC的内心I为圆心的一个圆，由点I向边BC,CA,AB引垂线，分别与Γ(I)交于点D，E，F，证明:AD，BE，CF三线交于一点[2].

分析与例3类似，可以采用类似的方法，也可以利用对称得到的点到直线的距离相等来直接计算相关角的正弦.

证明设∠CAD=α1，∠BAD=α2,∠ABE=β1,∠CBE=β2，∠BCF=γ1,∠ACF=γ2,d(X,YZ)表示点X到直线YZ的距离.因为D,E关于∠BCA的角平分线CI对称，所以

d(D,CA)=d(E,BC).

同理可得

d(E,AB)=d(F,CA)，d(F,BC)=d(D,AB).

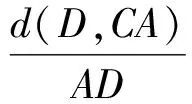
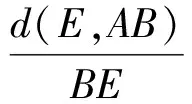
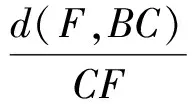
所以

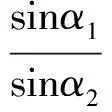
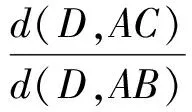
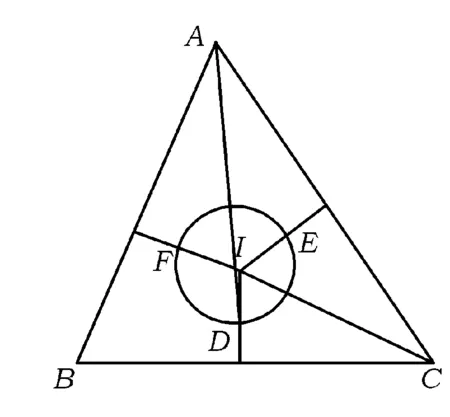
图4

由角元塞瓦定理的逆定理,可得AD，BE，CF三线交于一点.

利用角元赛瓦定理的例子很多，这里只就几个例子来说明利用我们掌握的知识，挖掘条件与结论之间的关系，以达到最终解决问题的目的.

[1] 2009保加利亚数学奥林匹克.国内外数学竞赛题及精解[J],李炘译.中等数学,2010(增刊):40-41.

[2] 2003年IMO中国国家集训队教练组.走向IMO数学奥林匹克试题集锦(2003)[M].上海：华东师范大学出版社，2003.