2011年希望杯全国数学邀请赛初三竞赛二试模拟卷(一)
2011-11-21施储
2011年希望杯全国数学邀请赛初三竞赛二试模拟卷(一)
一、选择题(共8小题,每小题5分,满分40分)
1.下列命题中,假命题是
( )
A.对角线互相垂直且相等的四边形是正方形 B.对角线相等且互相平分的四边形是矩形
C.对角线互相垂直平分的四边形是菱形 D.对角线互相平分的四边形是平行四边形
2.已知一次函数y=kx-k,若y随x的减小而减小,则该函数的图像经过
( )
A.第一、二、三象限 B.第一、二、四象限
C.第二、三、四象限 D.第一、三、四象限
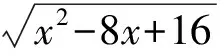
( )
A.x为任意实数 B.1≤x≤4 C.xgt;1 D.xlt;4
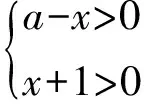
( )
A.a≥-1 B.agt;-1 C.a≤-1 D.alt;-1
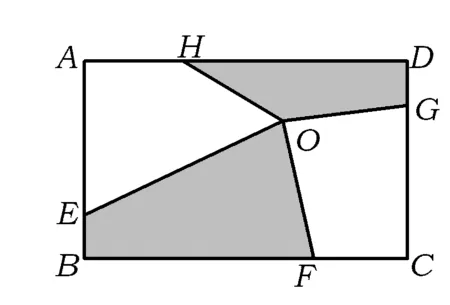
图1
5.如图1,在矩形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,点O在矩形ABCD内.若AB=4,BC=6,AE=CG=3,BF=DH=4,且四边形OGDH的面积为5,则四边形OEBF的面积为
( )
A.5 B.6 C.7 D.8
6.在一个棱长为4的立方体中放入直径为1的相同的球,可以放入最多的个数是
( )
A.66 B.64 C.75 D.73
7.如果关于x的方程ax2+(2a-1)x+a-5=0的2个根一个大于2、一个小于2,那么实数a的取值范围是
( )

8.甲、乙、丙、丁4个人做相互传球游戏,第1次甲传给其他3个人中的一人,第2次由拿到球的人再传给其他3个人中的一人(下同),这样的传球共进行了4次,则第4次仍传回到甲手中的概率为
( )
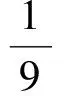
二、填空题(共8小题,每小题5分,满分40分)
9.已知AB为⊙O的直径,PA,PC是⊙O的切线,A,C为切点,∠BAC=30°,则∠P=________;若AB=2,则PA=________.
10.边长为3,4,5的2个直角三角形ABC,分别绕直角边AB和斜边AC旋转一周,得到2个不同的几何体P,Q,则这2个几何体的表面积分别是________和________.
11.二次函数y=x2+ax+a-2(a≠0)的顶点可能在第________象限.
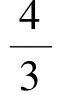
13.一个半径为1的圆O在一个边长为4的正方形ABCD内部随意滚动,设∠OAD=α,且tanα=k,则k的取值范围为________;又正方形的边长若为n(n是大于2的自然数),则k的取值范围为________.
14.东东准备给南南打电话,由于保管不善,电话本上南南的手机号码中有2个数字已模糊不清.如果用x,y表示这2个看不清的数字,那么南南的手机号码为139x370y580,东东记得这11个数字之和是20的整数倍,则x+y=________;东东一次拨对南南手机号码的最大概率是________.
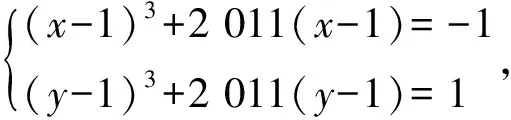
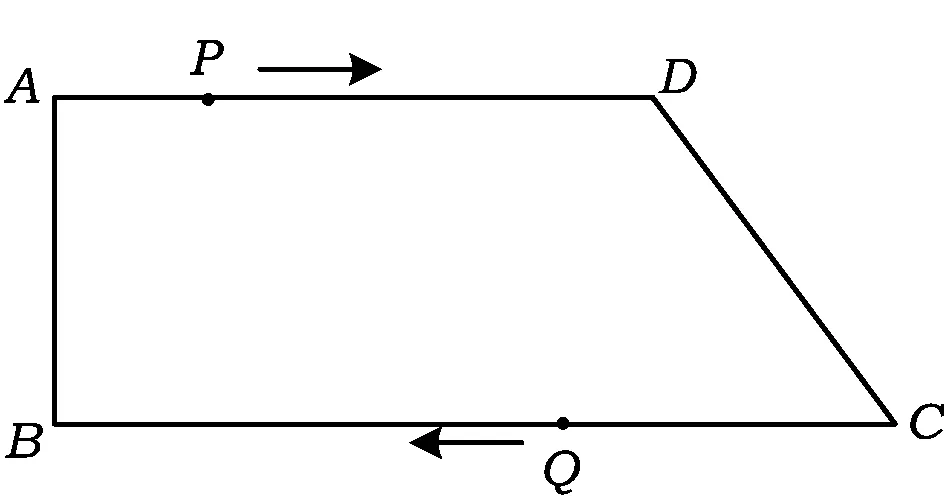
图2
16.如图2所示,在梯形ABCD中,AD∥BC,∠B=90°,AB=8 cm,AD=16 cm,BC=22 cm,点P从点A出发,以1 cm/s的速度向点D运动,点Q从点C同时出发,以2 cm/s的速度向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动.那么经过______s,四边形ABQP成为矩形;经过_____s,四边形PQCD成为等腰梯形;经过_____s,四边形PBQD成为菱形.
三、解答题(共2小题,每小题20分,满分40分)
17.有一个边长为6,8,10的直角三角形,现要求拼上一个一条直角边为8的直角三角形,使拼成的三角形成为一个等腰三角形,试画出各种不同拼法的草图,并求所拼出的等腰三角形的周长.

(1)当点D运动到与点A,O在一条直线上时,CD与⊙O相切吗?如果相切,请说明理由,并求出OD所在直线对应的函数表达式;如果不相切,也请说明理由.
(2)设点D的横坐标为x,正方形ABCD的面积为S,求出S与x的函数关系式,并求出S的最大值和最小值.
参考答案
1.A 2.D 3.B 4.C 5.B 6.A 7.C 8.D

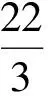
17.解拼接草图如图3所示,共4种.
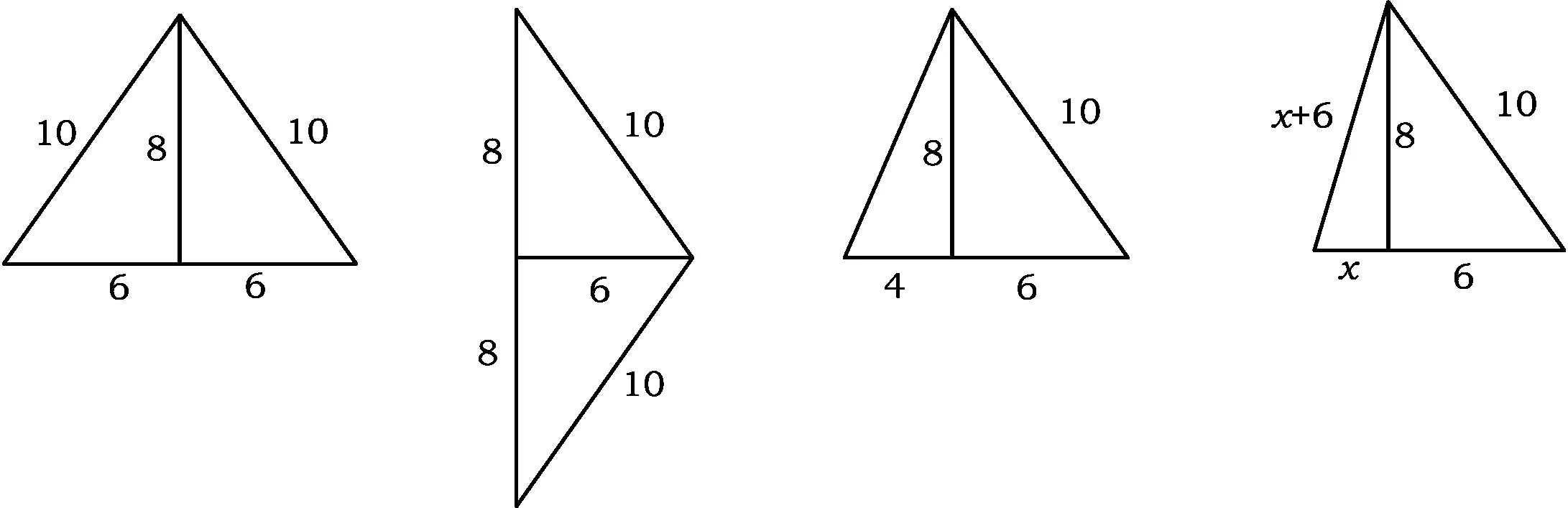
图3
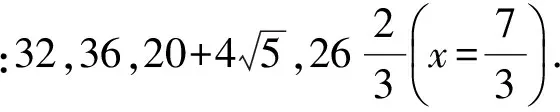
18.解(1)CD与⊙O相切.因为点A,D,O在一直线上,∠ADC=90°,因此∠CDO=90°,所以CD是⊙O的切线.当CD与⊙O相切时,有以下2种情况:
①切点在第二象限时(如图4所示),设正方形ABCD的边长为a,则
a2+(a+1)2=13,
解得
a=2或a=-3(舍去).
过点D作DE⊥OB于点E,则
Rt△ODE∽Rt△OBA,
因此
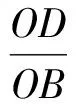
于是
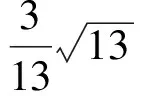
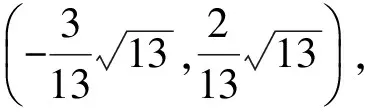
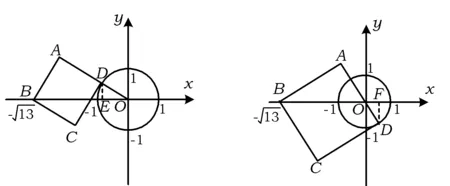
图4 图5
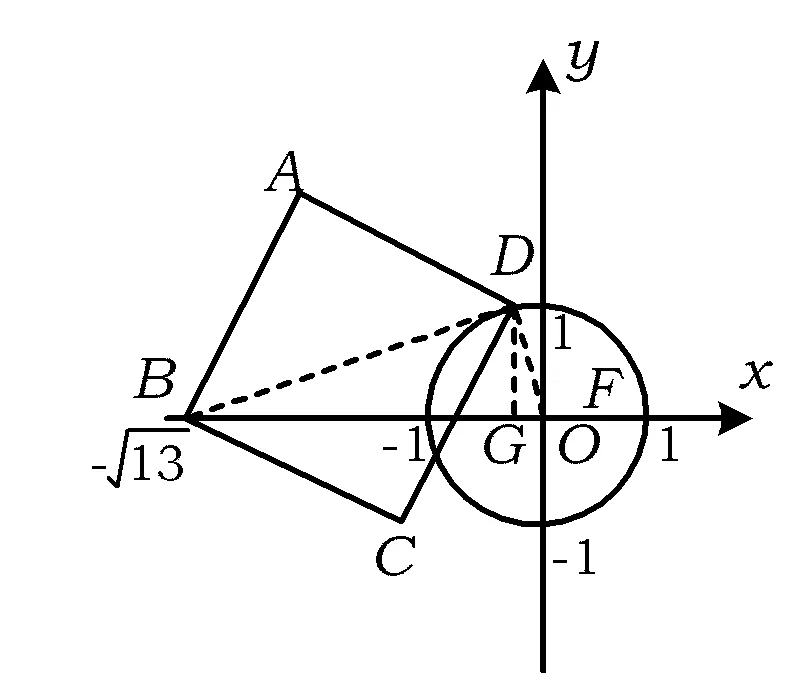
图6
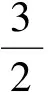
(2)如图6,过点D作DG⊥OB于点G,连结BD,OD,则
BD2=BG2+DG2=
(BO-OG)2+OD2-OG2=



(供稿人:施 储)
