关于中学概率内容的教与学

●

(中国科学技术大学统计系 安徽合肥 230022)

关于中学概率内容的教与学

●苏淳

(中国科学技术大学统计系 安徽合肥 230022)

概率统计内容进入中小学数学课堂是近几年的新生事物，是与国际接轨的一项举措，符合与时俱进的精神.

但是，综观整个中小学阶段的教学内容安排，却令人感觉杂乱无章，缺乏统一考虑和整体安排.有些内容反复出观，有些内容缺乏深度.

以下，笔者仅就个人的体会，谈两点看法.

1 古典概型与计数

现行中学数学课本的最大不足在于忽视基本功的训练，试图在沙滩上建高楼.在古典概型中不重视对概率计算方法的教学就是其中的一种表现，其结果是造成学生只会用繁杂的方法计算古典概率，既使学生学得无味，又凭空增加了学生的负担.

因为古典概型所涉及的统计试验都只有有限个可能的基本结果，所以引入一个符号Ω来表示所有可能的基本结果之集是一件轻而易举的事情.而且这样一来，样本空间、基本事件、随机事件的直观概念便自然而然地为学生所接受，为后面的学习打开了方便之门.这种既方便又有利的事情，现行中学课本却没有去做.

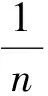
应当指出，如何正确利用式(1)计算概率，是大有讲究的.下面举例说明.

例1一个笼子里关着10只猫，其中有7只白猫、3只黑猫.把笼门打开一个小口，使得每次只能钻出1只猫.猫争先恐后地往外钻.如果10只猫都钻出了笼子，以Ak表示第k只出笼的猫是黑猫的事件，试求P(Ak)(k=1,2,…,10).

分析显然，如果用Ω表示10只猫出笼的所有不同的可能列队顺序构成的集合，那么Ak就是由所有符合条件的列队顺序所构成的子集.

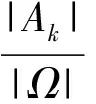
这是一种最容易被同学接受的解法.但是，由于使用的是排列模式计数，把10只猫视为10个不同的元素，然而猫有时是很难识别的，除了颜色易于区分之外，在颜色相同的猫之间往往很难分辨出谁是谁，因此在计算它们出笼的先后顺序时，未必能视为10个不同元素的排列.相反地，把同种颜色的猫看成相同的元素，似乎要更加合理一些.由此看来，不如采用不尽相异元素的排列模式计算出笼顺序.

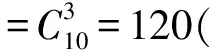
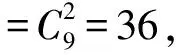
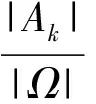
就运算过程而言，这种方法较之解法1要简单得多;就所说的道理而言，也无不当之处.最为重要的是：尽管采用了2种不同的计数模式计算|Ω|和|Ak|,但是计算出的概率值却是相等的.这就告诉我们，概率计算问题不同于普通的计数问题，在概率计算问题中，重要的不是采用何种计数模式来计算样本空间和随机事件中的样本点(基本事件)的数目，而是要保证对两者采用同一种计数模式.鉴于上述考虑，还可以给出猫出笼问题的其他解法.

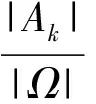
这样，我们又得到了与前面2种解法完全相同的结果.这个例子告诉我们：对于古典概型问题，可以有多种不同的解法，并且可以采用不同的计数模式计算样本点的个数.但是，必须对样本空间和随机事件采用相同的计数模式，并且能够给出合理的解释.

例2笼内关有6只果蝇，不慎混入2只苍蝇，只好把笼子打开一个小孔，让蝇子一只一只飞出去，直到2只苍蝇都飞出笼子，再关闭小孔.以X表示笼内所剩下的果蝇数目，求X的分布律.

分析这是一道建立在古典概型基础上的随机变量试题，其关键仍然是合理计算古典概率．

解X的取值集合为{0,1,…,6}，并且对任何k∈{0,1,…,6},(X=k)都是一个随机事件，它表示共飞走了8-k只蝇子，其中最后飞走的一只是苍蝇，在前7-k只蝇子中有一只是苍蝇.

可以设想所有蝇子都飞出了笼子，考察最后有多少只连续飞出的果蝇，这时的果蝇数目仍然是X，我们记Ak=(X=k).如果以Ω表示蝇子出笼的所有可能顺序的集合，那么Ak就是最后有k只连续飞出的果蝇的各种可能顺序所构成的子集.显然，可以利用排列模式计算|Ω|和|Ak|.但不如采用组合模式方便：

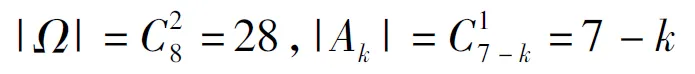
(在前7-k只蝇子中有1只是苍蝇)，因此

2 全概率公式应当成为中学概率教学的落脚点

中小学关于概率统计内容的教学前后跨越了10年之久，然而最后却始终未能引出全概率公式.全概率公式不仅是初等概率发展史中的里程碑，其意义与价值远远超越了历史的局限，迄今仍在概率统计的各个领域中发挥着无可替代的重要作用.

对于中学生来说，全概率公式并不难接受，相反，却能大大提高他们的解题能力，更能提高他们的学习兴趣.

例3有2个罐子，在第1个罐中放有7个红球、2个白球和3个黑球，在第2个罐中放有5个红球、4个白球和3个黑球.从第1个罐中随机取出1个球放入第2个罐中，再从第2个罐中随机取出1个球来.试求从第2个罐中随机取出的球为红球的概率.

分析这是一个我们从未遇到过的问题.在这个问题中，包含了2个相继进行的随机试验，并且第2个随机试验的结果受到第1个试验之结果的影响.

解分别以A1，A2，A3表示由第1个罐子取往第2个罐子的球是红球、白球和黑球的事件．显然这3个事件两两不交，并且它们之并就是Ω,因此

从而

(2)

由于A1，A2，A3都是第一个试验的结果，为计算它们的概率，将样本空间取为第1次取球的所有可能结果之集，并按古典概型计算之,因此

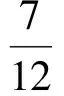
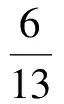
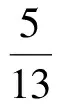
综上所述,可得

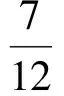
这种方法把一个较为复杂的概率计算问题分解为一系列易于计算的步骤.为了总结这个方法，先给出一个定义.

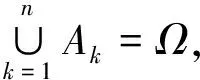
在必要时，可以把分划的概念推广到可列个事件(即n为+∞)的情形.

利用对样本空间Ω的分划，我们给出如下的概率计算公式.

定理1(全概率公式)设A1，A2，…，An是对样本空间Ω的一个分划，如果P(Ak)gt;0，k=1，2，…，n，则对任何随机事件B，都有

在可列情形下,相应地有：

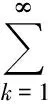
通过例1的解答，我们看到了全概率公式的威力．在使用该公式时，应当注意正确选择Ω的分划{Αk，k=1，2，…，n}.若选择不当，则难以达到简化计算的目的．

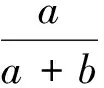
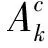
同理可得

于是由全概率公式得

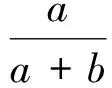
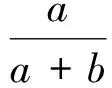
因此结论对一切n都成立．

例5甲、乙2人轮流抛掷一枚均匀的骰子．甲先掷，一直到掷出了1点，交给乙掷，而到乙掷出了1点，再交给甲掷，并如此一直下去．试求第n次抛掷时由甲掷的概率．

于是由全概率公式得

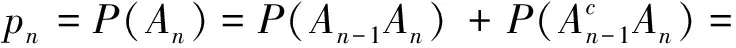
经过整理，将上式化为易于递推的形式

反复利用该式，并注意p1=1，得

因此

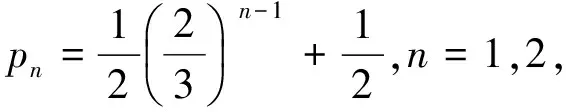
下面介绍一个有趣的问题，其解答可利用全概率公式.

例6包括甲、乙2人在内的2n名乒乓球运动员参加一场淘汰赛，第一轮将他们任意两两配对比赛，然后2n-1名胜者再任意两两配对进行第2轮比赛，如此下去，直至第n轮决出一名冠军为止.假定每一名运动员在各轮比赛中胜负都是等可能的,求甲、乙2人在这场比赛中相遇的概率.

解在参赛人数为2n时，记甲、乙2人在这场比赛中相遇的概率为pn，并记他们在第一轮比赛中就相遇的概率为qn.

下面对n进行讨论.若n=1，则一共只有甲、乙2个人参加比赛，他们一定在第1轮相遇，所以p1=q1=1.

若n=2，则有包括甲、乙2人在内的4个人参加比赛.分别以A和B记他们在第1轮和第2轮比赛中相遇的事件，于是

p2=P(A)+P(AcB)=

P(A)+P(Ac)P(B|Ac)=

q2+(1-q2)P(B|Ac).

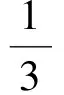
p2=q2+(1-q2)P(B|Ac)=

如上的结果使我们有理由猜测：对一切正整数n，都应当有

pk+1=P(A)+P(AcB)=

P(A)+P(Ac)P(B|Ac)=

qk+1+(1-qk+1)P(B|Ac).

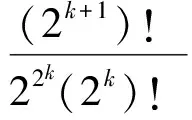
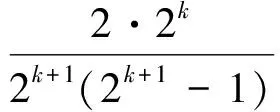
如果甲、乙2人在第1轮比赛中没有相遇，那么要使他们在后续的比赛中相遇，就必须2个人在第1轮比赛中双双战胜对手，同其余2k-2名胜者一起进入下一轮比赛.而从此时开始便是2k名运动员按照原来的比赛规则进行比赛.因此只要甲、乙2人都能进入后续的比赛，那么他们在后续比赛中相遇的概率就是pk，于是

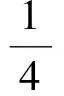
结合归纳假设即知

pk+1=qk+1+(1-qk+1)P(B|Ac)=

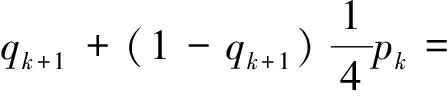
当n=k+1时,结论仍然成立.

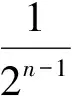
在上述解答中，我们都是以A和Ac(即甲、乙2人是否在第1轮相遇)作为对Ω的分划．这种对分划的选取方式不仅有利于处理n=2的情形，而且有利于运用归纳假设进行归纳过渡.