高效课堂之“架”“导”“智”

钱嘉珺

［摘  要］ 打造高效课堂是课堂教学的最高目标，也是每个数学教师不懈的追求. 文章结合“探索线段的比例关系”的专题复习课，从课堂中的“架”“导”“智”这三个方面着手，探讨了构建高效复习课堂的基本策略.

［关键词］ 高效课堂；线段的比例关系；复习课

打造高效课堂是课堂教学的最高目标，也是每个数学教师不懈的追求. 事实上，对于高效并没有统一的界定，它仅仅是相对于低效、无效和负效而言的一个概念. 关于高效课堂的构建，不少一线教师进行了深入研究. 笔者从课堂中的“架”“导”“智”这三个方面着手，结合“探索线段的比例关系”的专题复习课，探讨构建高效复习课堂的基本策略.

“探索线段的比例关系”的专题

复习课的教学过程

1. 备课中的点滴思考

课前，教师深入了解了具体学情，获悉授课班级的学生已经学习了相似三角形的判定与性质，尽管没有接受相关的综合训练，但也有了较为扎实的基础知识，且成绩优异. 当然，在前面的学习中对于线段倍分关系、和差关系的问题他们虽多有接触，但在探寻线段比例关系这一环节还是仅凭感觉，并没有系统的思考路径. 一些中等生表示不太擅长线段比例关系的证明以及计算问题，还有一些学困生表示找不到探究入口. 正是基于以上现象，笔者在备课中思考了以下问题：

问题1：本课的教学目标是什么？

通过本课的教学，要让学生学会探究线段的比例关系的方法，还要进一步延伸到求线段长度、两条线段的比值或乘积等问题，以深化思维，培养高阶思维能力.

问题2：建立比例关系的思路有哪些？

灵活添加辅助线可以说是建立线段比例关系的一个巧妙思路，一般来说有定型法和等量代换法这两种常用的证明方法.

问题3：该确立怎样的教学思路？

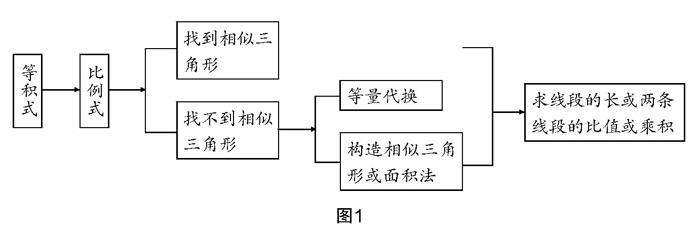
首先，可以借助引例和例题，让建立线段比例关系的一般性方法与思路浮出水面；进一步地，在学以致用中将其逐步延伸至求线段长度、比值等一系列问题中去. （具体教学框架如图1所示）

教学过程

1. 旧知重现，感受比例

问题1：已知l∥l∥l，结合图2写出3个不同的比例式，并试着说一说两个三角形相似的判定和性质.

设计说明  将平行线分线段成比例及两个三角形相似的判定和性质用问题的形式再现，凸显问题解决的意识，让学生在问题的解决中感悟平行线中线段的比例关系，同时为后续的学习打下坚实的基础.

2. 以问促思，回归本源

问题2：如图3，已知平行四边形ABCD的边AD上有一点E，连接BE并延长后与CD的延长线交于点F.

（1）据△_____∽△_____，得出=；

（2）据△_____∽△_____，得出=.

问题3：如图4，已知Rt△ABC中，有CD⊥AB于点D，∠ACB=90°，证明：CD2=AD·BD.

设计说明  教师继续将思维融入问题，让学生在深度思考后先找出需要证明相似的两个三角形的方法，再体会成比例线段的本源. 在此过程中，教师也不失时机地将竖定法渗透进来，让学生在两个问题的巩固下获得对“横定法”和“竖定法”更加全面、深刻的认识. 最后，自然是通过归纳解题思路来深化探寻证明两个三角形相似的方法与思路，同时提炼建立线段比例关系的雏形.

3. 例题引领，深化认识

例1如图5，已知Rt△ABC中，正方形DMNE的顶点D，E，M，N分别在边AC，BC和AB上，且∠C=90°，证明：MN2=AM·NB.

例2如图6，已知△ABC中，CD为∠ACB的角平分线，且AC

设计说明  教师针对性地设计两道典型例题的目的有二：其一，通过例1引领学生深入探索当题目不满足一般性解法条件时需运用等线段进行替换；其二，通过例2引领学生探索当题目满足一般性解法，而两个三角形并无相似关系且图形中也无相似三角形时需构造相似三角形. 这样的两道典型例题，极好地为学生积累了解题经验.

4. 练习体悟，理解方法

练习：如图7，已知△ABC中，边BC上有一点D，边AB上有一点F，且AD，CF交于点E. 若点E为中线AD的中点，试求出的值.

设计说明  教师以一道求线段比值的练习题，完美地拓展了比例关系的应用，让学生在解决问题中真正获得求解等积式或比例式问题的一般方法与思路. 除此之外，教师还设计了变条件编题的探究活动，让学生尝试寻找更多解法，最终学生在教师的指引下梳理归纳得出证明等积式或比例式的一般方法与思路，同时深化了认识.

5. 总结提炼，内化思想

师生共同总结提炼，回顾各个环节中的板书，生成完善的框架式小结（即图1所示的教学框架图），以获得完善的比例关系问题的解题方法.

设计说明  梳理证明线段比例关系问题的一般方法，并将这种解题思路渗透进学生的思想中去，让学生的思维与情感得到升华.

关于本课的一点思考

1. 高效课堂之“架”

“架”即架构，指的是高效课堂的基本框架、基本标准. 本课中，教师站在一个整体的高度，从高效课堂的基本框架出发设计大问题导学，让学生在问题的引领下深入思考、深度探究和合作学习，让学生在自主学习中习得解决问题的一般方法和思路，并内化为自己的思想. 整个教学过程中，学生的思维是活跃的，思路是开放性的，这样的课堂显然是高效的课堂.

2. 高效课堂之“导”

“导”即引导，指的是高效课堂中的引导和导学. 好的引导来自教师对学科好的钻研、对学科内容好的把握以及对学科本身好的认知等. 而正是因为这多种因素的作用，切实影响着学生对一节课的接受程度，这些因素在课堂上的综合呈现也直接影响到课堂效率. 本课中，教师在课前深钻教学内容，并多番探究学情，从而为之后的“导”打下了坚实的基础. 纵观整节课的教学过程，正是由于“导”得适当，“导”得及时，才能让学生通过不断体悟获得解题思想，进而内化为自身的一种核心素养.

3. 高效课堂之“智”

“智”即智慧，指的是高效课堂势必是充满生机与智慧的. 在课堂上，无论是教师的灵机一动还是学生的灵活思维都是智慧的表现. 叶澜教授曾对评判一节课是否是好课提出了“五实”标准，而其中最为重要的“丰实”，就是需要课堂具有生成性. 本课中，教师积极引导，学生主动参与，不仅有了知识生成，也有了智慧生成. 在每个教学环节中，教师都会抛出为学生搭建思考平台的核心问题. 例如，在学生完成练习题后，教师立刻抛出问题“通过解答本题，你觉得运用探求线段比例关系的一般方法还有哪些价值？”这样，则可以让学生在智慧的引领下提高发散思维能力和归纳总结能力.

当然，构成高效课堂的要素很多，但本文提出的“架”“导”“智”是高效课堂的重点要素，没有架构的课堂无法互动自如，没有引导的课堂无法引发学生的共鸣，没有智慧的课堂无法激起思维火花. 高效课堂是个永恒的话题，高效课堂的探究之路需要我们持之以恒地加以探索.