APOS理论在初中数学概念教学中的实践研究

［摘  要］ APOS理论是从“操作、过程、对象、图式”四个阶段讨论数学学习的心理结构与心理机制. 研究者从APOS理论的本质与功能定位、概念教学中的优势、实施原则出发，以“变量与函数”的概念教学为例展开实践与思考.

［关键词］ APOS理论；概念；函数

《义务教育数学课程标准（2022年版）》（简称新课标）强调数学教学要重视数学概念的心理建构，关注学生在学习过程中的思维活动情况，这对培养与发展数学核心素养具有重要意义. APOS理论是由美国学者杜宾斯基等人提出的与概念学习相关的一种理论，该理论着重强调概念教学过程中对学生的心理建构，这与新课标提出的理念有着惊人的相似之处.

APOS理论的本质与功能定位

APOS理论从本质上来说就是从“操作、过程、对象、图式”四个方面讨论数学学习的心理结构与心理机制. 而在实际应用时，仍有不少教师对“心理结构”与“心理机制”的区分不够明确. 具体来说，心理结构属于一种静态的状态，而心理机制则属于动态的过程，心理机制可以让一个人从这种心理结构转换成另一种心理结构.

与之相应，“心理结构”与“心理机制”促使我们从两个方面对APOS理论进行定位. 第一点，该理论具备诊断功能，它可对个体对数学概念的理解程度与思维发展情况进行调查. 在此过程中，APOS理论为诊断学习是否构成心理结构服务，其诊断结论为教学评价与反思的依据；第二点，该理论具有解释功能，它能从心理机制的角度解释学习者对知识的建构情况，在此过程中，APOS理论对教学具有指导意义，是进一步研究的依据.

APOS理论于概念教学的优势

概念是数学的基础，随着新课改的推进，对概念教学的要求越来越高，与概念教学相关的理论也应运而生. APOS由操作（Action）、过程（Process）、对象（Object）、图式（Schema）四阶段的英文首字母组成，该理论认为个体在数学学习过程中经过思维操作、过程与对象等阶段之后，学习者可在建构与反思的基础上将所学内容组成图式，因而厘清问题的本质并解决问题.

在建构主义理论的基础上，引导学生自主感知概念与背景之间的联系更利于概念的抽象，这对提升学生对概念的记忆、理解与应用具有重要价值与意义. 因此，APOS理论对提升初中数学概念教学的成效具有显著优势.

APOS理论在概念教学中的实施原则

1. 灵活性原则

APOS理论所具备的操作、过程、对象与图式四个阶段并非为单一的线性关系，它与教学内容特点、学生的认知水平、智力发展情况、学习经验与能力等有着重要关联. 灵活调控各个环节，不仅能有效提高教学效率，对发展学力也有重要意义. 如将某个环节实施两次或删减均可取，也可以根据教学实际情况从对象阶段返回到活动阶段. 鉴于初中阶段学生存在较大的差异性，教师在教学时，需酌情分析，灵活择取恰当的阶段提高教学成效.

2. 主体性原则

不论是APOS理论还是新课标的要求，都强调学生在课堂中的主体地位. APOS理论强调学生是知识的建构者，所有的外界活动都是促使学生思维结构发展的基础. 鉴于此，在教学时，教师应关注教学环节的设计，想方设法引导学生主动参与活动过程，并通过自主探索获得相应的感悟，以从真正意义上体现学生为课堂的主人.

3. 探究性原则

APOS理论本身就具有探究性特征，其探究主要包含新知的探索与教学过程的探究. 教师可在教学伊始结合学生的实际认知水平与学习经验创设具有探究性的情境，以激发学生的探索欲，促使学生亲历概念抽象过程，获得良好的学习体验，以促进知识的融会贯通.

APOS理论在概念教学中的应用

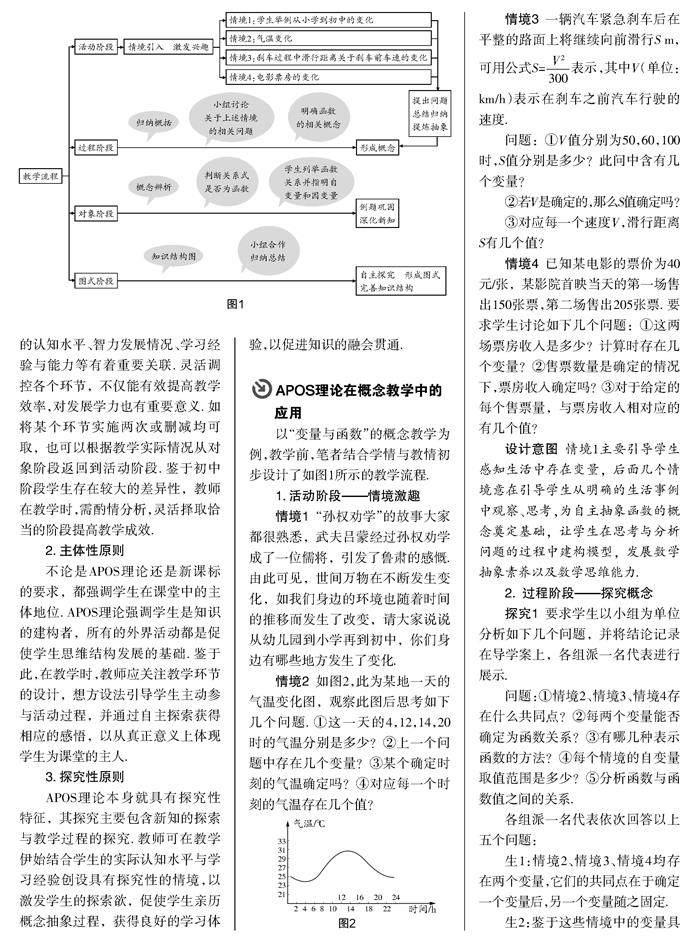
以“变量与函数”的概念教学为例，教学前，笔者结合学情与教情初步设计了如图1所示的教学流程.

1. 活动阶段——情境激趣

情境1“孙权劝学”的故事大家都很熟悉，武夫吕蒙经过孙权劝学成了一位儒将，引发了鲁肃的感慨. 由此可见，世间万物在不断发生变化，如我们身边的环境也随着时间的推移而发生了改变，请大家说说从幼儿园到小学再到初中，你们身边有哪些地方发生了变化.

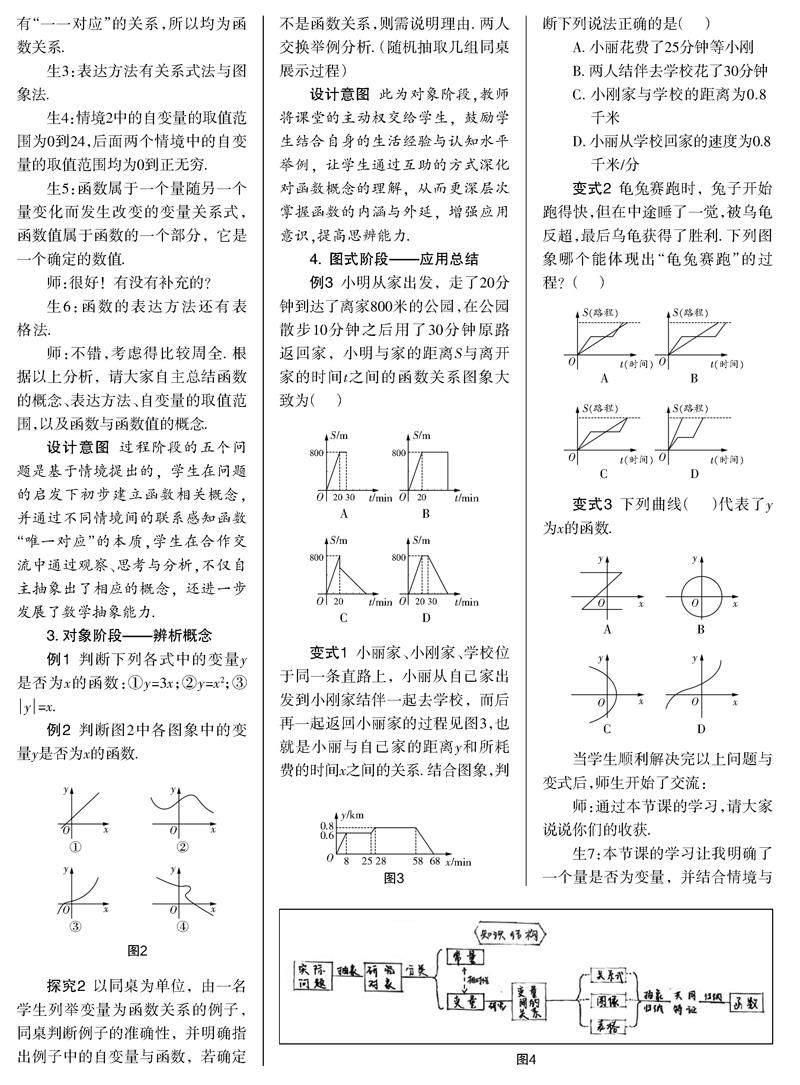
情境2如图2，此为某地一天的气温变化图，观察此图后思考如下几个问题. ①这一天的4，12，14，20时的气温分别是多少？②上一个问题中存在几个变量？③某个确定时刻的气温确定吗？④对应每一个时刻的气温存在几个值？

情境3一辆汽车紧急刹车后在平整的路面上将继续向前滑行S m，可用公式S=表示，其中V（单位：km/h）表示在刹车之前汽车行驶的速度.

问题：①V值分别为50，60，100时，S值分别是多少？此问中含有几个变量？

②若V是确定的，那么S值确定吗？

③对应每一个速度V，滑行距离S有几个值？

情境4已知某电影的票价为40元/张，某影院首映当天的第一场售出150张票，第二场售出205张票. 要求学生讨论如下几个问题：①这两场票房收入是多少？计算时存在几个变量？②售票数量是确定的情况下，票房收入确定吗？③对于给定的每个售票量，与票房收入相对应的有几个值？

设计意图情境1主要引导学生感知生活中存在变量，后面几个情境意在引导学生从明确的生活事例中观察、思考，为自主抽象函数的概念奠定基础，让学生在思考与分析问题的过程中建构模型，发展数学抽象素养以及数学思维能力.

2. 过程阶段——探究概念

探究1要求学生以小组为单位分析如下几个问题，并将结论记录在导学案上，各组派一名代表进行展示.

问题：①情境2、情境3、情境4存在什么共同点？②每两个变量能否确定为函数关系？③有哪几种表示函数的方法？④每个情境的自变量取值范围是多少？⑤分析函数与函数值之间的关系.

各组派一名代表依次回答以上五个问题：

生1：情境2、情境3、情境4均存在两个变量，它们的共同点在于确定一个变量后，另一个变量随之固定.

生2：鉴于这些情境中的变量具有“一一对应”的关系，所以均为函数关系.

生3：表达方法有关系式法与图象法.

生4：情境2中的自变量的取值范围为0到24，后面两个情境中的自变量的取值范围均为0到正无穷.

生5：函数属于一个量随另一个量变化而发生改变的变量关系式，函数值属于函数的一个部分，它是一个确定的数值.

师：很好！有没有补充的？

生6：函数的表达方法还有表格法.

师：不错，考虑得比较周全. 根据以上分析，请大家自主总结函数的概念、表达方法、自变量的取值范围，以及函数与函数值的概念.

设计意图过程阶段的五个问题是基于情境提出的，学生在问题的启发下初步建立函数相关概念，并通过不同情境间的联系感知函数“唯一对应”的本质，学生在合作交流中通过观察、思考与分析，不仅自主抽象出了相应的概念，还进一步发展了数学抽象能力.

3. 对象阶段——辨析概念

例1判断下列各式中的变量y是否为x的函数：①y=3x；②y=x2；③y=x.

例2判断图2中各图象中的变量y是否为x的函数.

探究2以同桌为单位，由一名学生列举变量为函数关系的例子，同桌判断例子的准确性，并明确指出例子中的自变量与函数，若确定不是函数关系，则需说明理由. 两人交换举例分析. （随机抽取几组同桌展示过程）

设计意图此为对象阶段，教师将课堂的主动权交给学生，鼓励学生结合自身的生活经验与认知水平举例，让学生通过互助的方式深化对函数概念的理解，从而更深层次掌握函数的内涵与外延，增强应用意识，提高思辨能力.

4. 图式阶段——应用总结

例3小明从家出发，走了20分钟到达了离家800米的公园，在公园散步10分钟之后用了30分钟原路返回家，小明与家的距离S与离开家的时间t之间的函数关系图象大致为（     ）

变式1小丽家、小刚家、学校位于同一条直路上，小丽从自己家出发到小刚家结伴一起去学校，而后再一起返回小丽家的过程见图3，也就是小丽与自己家的距离y和所耗费的时间x之间的关系. 结合图象，判断下列说法正确的是（   ）

A. 小丽花费了25分钟等小刚

B. 两人结伴去学校花了30分钟

C. 小刚家与学校的距离为0.8千米

D. 小丽从学校回家的速度为0.8千米/分

变式2龟兔赛跑时，兔子开始跑得快，但在中途睡了一觉，被乌龟反超，最后乌龟获得了胜利. 下列图象哪个能体现出“龟兔赛跑”的过程？（   ）

变式3下列曲线（   ）代表了y为x的函数.

当学生顺利解决完以上问题与变式后，师生开始了交流：

师：通过本节课的学习，请大家说说你们的收获.

生7：本节课的学习让我明确了一个量是否为变量，并结合情境与实例理解了函数的概念以及两个变量间“一一对应”的关系.

师：非常好！现在请大家结合导学案与本节课所探索的内容，以小组为单位画出知识结构图.

（学生自主画图，教师择取学生的作品并投影展示，如图4）

设计意图图式阶段的主要作用在于整合所学知识，完善知识结构. 因此，基于例题与变式探索，引导学生自主总结归纳，通过对知识结构图的绘制进一步梳理本节课所学内容，这种教学方式可进一步发展学生的整合能力与创新意识.

教学思考

1. 活动阶段应注重情境创设

践行APOS理论的初始环节，关键在于吸引学生的注意力，激活学生的探索欲. 对于活动情境的创设，可从学生的生活背景与认知经验出发，通过恰当的情境引起学生的探索欲. 同时要关注情境与教学内容的关联度，避免为了完成任务而创设情境. 本节课的四个情境是在充分了解学情的基础上创设的，有效点燃了课堂气氛，激活了学生的探索欲，为教学奠定了基础.

2. 过程阶段可适当加深难度

过程阶段是教学的核心，以促使学生自主抽象概念为目标. 因此，教师的关键任务在于深化活动内容，帮助学生抽象并理解概念，让不同层次认知水平的学生都能通过恰当的活动体验概念的形成过程. 同时，适当增加问题的深度还能更好地激发学生的潜能，提升学生的抽象素养.

3. 对象阶段需对应概念内涵

此阶段关键在于提升学生对概念内涵与外延的理解，需引导学生从全方位细化对概念的认识. 为了有效提升学生在此过程中的思维能力，教师可在该环节选择恰当的方法帮助学生巩固对概念的认识，这对提升学生的数学推理能力具有无可替代的作用.

4. 图式阶段需注重完善结构

践行APOS理论的最后一个阶段，关键在于提升学生的应用与整合能力. 因此，教师可鼓励学生以分组合作的方式对一节课的教学内容、研究方法、数学思想等进行总结归纳. 当然，对不同认知水平的学生可允许用不同的方式进行总结，这也是提升学生创新能力的基础.

总之，APOS理论应用在概念教学中可从真正意义上优化教学操作策略，但在践行该理念时需结合具体情况进行，而非固定不变的模式. 从该理论的四个阶段来看，这是一种不断完善学生认知结构的理念，对发展学生的数学核心素养具有重要意义.

基金项目：江苏省教育科学“十四五”规划重点课题“新课标背景下APOS理论在初中数学概念教学中的实践研究”（B/2022/03/252）. 作者简介：刘勤凤（1984—），硕士研究生，中小学高级教师，从事初中数学教育教学工作.