初中数学探究课的构建及反思

［摘  要］ 高效的探究课可以在全面了解学生学情的基础上，从四个方面进行构建，从而提高数学探究式教学的效率，完成课堂教学目标，加深学生对数学知识形成过程的理解，培养学生的数学核心素养，提高学生发现问题和解决问题的能力.

［关键词］ 探究课；课型构建；数学核心素养

探究式学习是新课改提倡的一种重要的教学方式. 它是在充分尊重学生的主体地位的基础上，积极调动学生的学习激情，使学生经历系统的、完整的问题解决过程，发展学生的数学核心素养. 数学探究活动，应根据学习内容的特点设计，以满足学生对生活的实际认知，带动学生对数学知识发生和发展过程的主动探究. 因此，高效率的探究课的建设就变得越来越重要了. 本文以“三角形中位线”为教学案例，进行了探究课的构建及反思，整理如下，供大家一起研讨交流.

教材分析

本节课内容选自北师大版八年级下册第六章第3节，学生在初一学习了全等三角形，初二学习了平行四边形、平面直角坐标系等相关知识. 基于这样的学情，高效的探究课可从操作探究、观察猜想、推理论证、学以致用这四个方面进行数学课型构建.

教学过程

1. 操作探究，激活思维

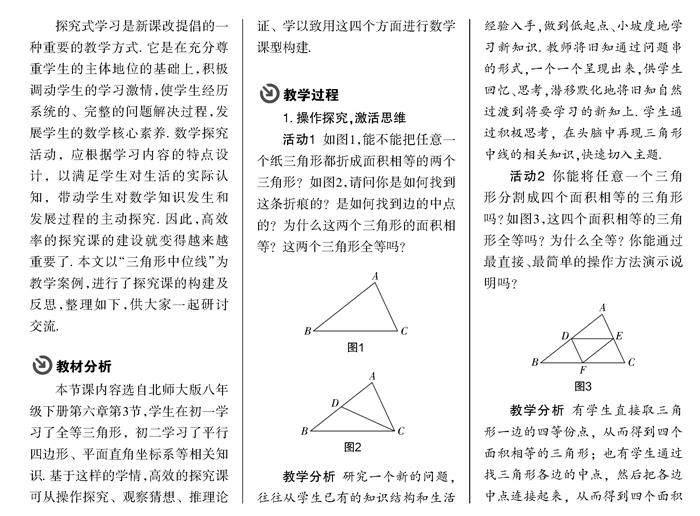
活动1  如图1，能不能把任意一个纸三角形都折成面积相等的两个三角形？如图2，请问你是如何找到这条折痕的？是如何找到边的中点的？为什么这两个三角形的面积相等？这两个三角形全等吗？

教学分析  研究一个新的问题，往往从学生已有的知识结构和生活经验入手，做到低起点、小坡度地学习新知识. 教师将旧知通过问题串的形式，一个一个呈现出来，供学生回忆、思考，潜移默化地将旧知自然过渡到将要学习的新知上. 学生通过积极思考，在头脑中再现三角形中线的相关知识，快速切入主题.

活动2  你能将任意一个三角形分割成四个面积相等的三角形吗？如图3，这四个面积相等的三角形全等吗？为什么全等？你能通过最直接、最简单的操作方法演示说明吗？

教学分析  有学生直接取三角形一边的四等份点，从而得到四个面积相等的三角形；也有学生通过找三角形各边的中点，然后把各边中点连接起来，从而得到四个面积相等的三角形. 通过亲身经历动手折纸和逐步探究问题串，层层深入，复习旧知，引出新知——三角形的中位线.

活动3  如图 3 ，取三角形各边的中点，并将中点连接起来，可把该三角形分割成四个全等的三角形. 这里的线段DE，DF，EF是三角形的另一类特殊的线段——三角形的中位线.

教学分析  在逐步探究过程中，自然而然地引出三角形的中位线的概念. 教科书上基本是直接给出中位线的概念，省略了知识产生和发展的过程. 这对于学生来说，缺乏一个对知识产生、发展的认知过程. 如果把知识或方法作为结果直接告诉学生，虽然节省了不少时间，但长此以往，越扔越多，学生很难在头脑中形成良好的认知结构［1］.因此，课堂教学应当呈现知识产生、发展的过程，调动学生自己去发现、去概括、去得出结论，既能培养学生的创新精神，又能使学生的观察能力、抽象能力、数学核心素养得到更好的培养，起到激发学生探究数学实际问题的兴趣.

2.观察猜想，发展思维

问题1  观察图4，猜想线段DE与BC边有怎样的位置关系和数量关系.

问题2  如何去求证你的猜想呢？你能借助手头上的工具，比如直尺、圆规、量角器等，去验证它吗？

问题3  通过几何画板所画的图形（如图5）去度量验证一定准确吗？请问如何从理论上证明这个定理？

教学分析  通过问题1引导学生去观察线段DE与BC边的位置关系和数量关系，接下来进行猜想. 猜想是解决探究问题最核心的一步，想要解决这个问题，学生会想到最简单的、最原始的“度量验证”的方法. 在这个观察猜想的过程中，可以培养学生的观察能力和创新能力，锻炼学生大胆猜想的能力. 当学生探究出DE平行且等于BC的一半时，能很好地激发学生的数学成就感，培养学生的数学学习兴趣. 当然，为了进一步培养学生严谨的科学态度，需要对猜想进行理论上的证明.

3. 推理论证，提升思维

如图6，已知线段DE是△ABC的中位线. 求证：DE∥BC，DE=BC.

证法1：如图7，延长DE至点F，使得EF=DE，连接CF. 易证△ADE≌△CFE（SAS），可得四边形BDFC为平行四边形，从而定理得证.

证法2：建立如图8所示的平面直角坐标系. 设A（a，b）， B（0，0），C（c，0），则 D，，E，，DE=，所以DE∥BC，DE=BC.

证法3：视频展示中国魏晋时期数学家刘徽的“割补法”与西方国家欧几里得的“面积法”对该定理的证明. 如图9，分别取△ABC中AB，AC两边的中点D，E，连接DE，得到△ABC的中位线DE，再分别过点B，C作DE的垂线，与DE的延长线交于点M，N，最后过点A作AH⊥DE于H. 易证△AHE≌△CNE，△ADH≌△BDM，从而易得S=S，故DE∥BC，DE=BC. 这可以说明，三角形的中位线与底边的关系，我国古代数学家早就知道了. 在《几何原本》中有另一种证明方法：如图 10 ，在△ABC 中， D 和 E 分别是AB和AC的中点，连接 DE、BE 和DC. 易知S=S，S=S，则S=S，故DE∥BC. 另一方面，因为S=S=2S，而△BDE和△EBC是等高的，所以DE=BC ［2］.

教学分析  多种证明方法的研究，可以启迪学生的逻辑思维能力. 证法2将几何问题代数化，将形转化为数来研究，这是解决几何问题的又一种方法——解析法；证法3将数学史融入课堂中，学生既可以了解数学文化，又能体会古人的智慧结晶.

4. 学以致用，深化思维

练习1  如图11，需测量河流宽AB的长度，可以先取一个如图所示的点C，连接CA，CB，分别在线段CA，CB上取中点D，E，连接DE，测得DE=150 m，则可得A，B之间的距离为______ m.

练习2  如图12，点D，E，F分别为AB，BC，AC边的中点，若C=30，则C=______.

练习3  如图13，在正方形ABCD中，AB=4，E，F分别是边AB，BC的中点，连接AF，DE，P，Q分别是AF，DE的中点，连接PQ，则PQ=______.

教学分析  学习了新知识，能将其应用于生活实际，可谓“数学来源于生活，同时也应用于生活”. 能让学生对数学产生浓厚的学习兴趣，促使学生不断去研究数学，展现数学高于生活的另一面.

5. 布置作业，巩固思维

设计作业练习题目，引导学生变式训练，有针对性地整合练习题，串联起零散的知识点. 设计一题多解、一题多变的分层作业，有针对性的训练，可达到深入理解、牢固掌握、灵活应用知识的效果.

教学反思

数学家波利亚曾说过，数学教育的一个主要目的就是教会学生如何去思考问题，培养学生解决问题的能力［3］. 初中数学探究课的构建形式，可以更好地促进学生去思考问题，彰显学生主动探究、学习数学的特征.

1. 探究课的构建凸显了知识的整体性和逻辑性

本节探究课，学生从数学知识、研究思路、研究方法等方面都有各自的收获. 在探究过程中，证明了三角形中位线定理，培养了学生数形结合、转化与化归数学思想方法和数学逻辑思维能力. 在研究思路上，从定义到性质、定理、运用等各个方面，使学生对三角形中位线定理的理解更深入，形成自己的知识网络体系. 在研究方法上，通过调动学生的积极性从观察到猜想，再到验证和应用，可以培养学生的数学兴趣. 这样进行探究课的呈现与推进，充分揭示了知识发生、形成的过程，使学生对知识的掌握更深刻、更牢固，增强了学习的成就感，树立了自信心.

2. 探究课的构建体现了学习的主动性和活动性

本节课以动手操作和问题串的形式展开教学活动，在“操作探究、观察猜想、推理论证、学以致用”这四个过程中，促使学生根据教师创设的情境分析问题、探究问题、解决问题. 整个教学过程就如数学家弗赖登塔尔所提倡的：“让学生经历数学化. ”这说明数学化的过程比结果更重要. 因此，探究课应当更注重“做”数学的过程，让学生经历数学知识发生、发展的过程，从而激发学生学习兴趣，促使学生掌握数学问题本质.

3. 探究课的构建呵护了学生探索知识的积极性

在探究课中，教师应当正确对待每一个学生探究出来的结论. 尽管有些结论是浅显的，甚至是错误的，但要知道出错是宝贵的，一学就会的东西的价值不大，只有让学生经历探索的辛苦和不容易，才能深刻体会成功的喜悦. 同时要注意学生探索的问题不能太难，让学生跳一跳够得着就行，最高明的教育是鼓励、激励，同样一个问题，鼓励学生从不同的角度去分析，用不同的方法去解决，肯定他们的成绩，哪怕只做对一步，也要让他们有信心想下去，有去试一试的欲望.

通过探究课的教学实践，笔者认为，应当将数学的本质、思想、方法渗透到探究程中，以数学知识的生成为起点，构建学生探究学习的基本框架，逐步培养学生的数学思维品质和数学核心素养，以适应个人终身发展和社会发展的需要.

参考文献：

［1］卢莲华.关于优化三角形中位线课堂教学方法的思考［J］. 广西教育学院学报，2000（03）：144-147.

［2］李铁，严达强，张晓斌. 数学史有效融入课堂教学的若干思考［J］. 中学数学教学参考，2020（23）：17-20.

［3］张扬.单元探究性教学的实践及思考——以“一元二次方程的解法”为例［J］. 中学数学教学参考，2021（35）：8-10.

［4］郭文忠. 探究性学习的教与学——“三角形中位线”的教学［J］. 井冈山大学学报，2004（05）：96-99.

作者简介：邱小伟（1991-），硕士研究生，中学一级教师，从事初中数学教学工作.