探究数形结合思想在初中数学解题中的运用路径

2024-04-16魏莉红

数学之友 2024年1期

魏莉红

摘要：较小学数学相比，初中数学在解题方面的难度有所增加，且逻辑性和系统性也更强.对此，很多学生在面对复杂的解题时，由于缺乏对数形结合思想的理解与运用，往往手足无措，没有解题思路，导致解题能力得不到提高.基于此，本文在概述初中数学解题运用数形结合思想的基础上，着重分析数形结合思想在初中数学不同类型解题中的运用路径，以期为广大一线初中数学教师提供教学参考.

关键词：数形结合思想；初中数学；解题

近年来，随着基础教学改革的推动与实施，中考在数学知识考核方面也发生了明显的变化，即考核内容更加丰富，考核方式也更为灵活.这种转变也意味着初中数学教师在日常教学中，要从根本上把握数学知识结构体系，通过传授有效的解题思维为学生理清知识脉络，使学生快速地理解并掌握解题的思想和方法.数形结合思想是初中数学学习中重要的思维方法之一，对于解决数学问题起着不可或缺的关键作用，具备这一解题思维，能够使学生在面对复杂的数学题时游刃有余.因此，教师要充分地认识到数形结合思想在初中数学解题中的重要性及必要性，并借助数形结合思想开拓学生的思维，发展学生的几何直观能力和解决问题能力.

1 数形结合思想概述

1.1 数形结合思想

数学家华罗庚曾提出：“数形结合百般好，割裂分家万事休.”数学的基本内容就是围绕“数”与“形”进行学习和研究，“数”指的是数量以及数与数之间的抽象关系，“形”指的是图形以及图形的概念.数形结合思想就是将原本存在本质区别的“数”与“形”相互结合并转化，通过分析二者之间的关系找到解题的思路和方法.具体来说，当前数形结合思想在解题中常用的方法有两点：第一，借助图形的直观性来得出数字之间的逻辑关系，将抽象的知识具象化；第二，使用数字来填补图形中缺失的主要信息，从而使图形间的关系更加清晰明了，将原本复杂的数学题目变得简单化.

1.2 初中数学解题中运用数形结合思想的意义

首先，增加数学解题教学的趣味性.数学学科的主要学习内容就是研究数量的抽象关系与空间的概念关系，因此在初中数学学习中，学生最应具备的数学思维能力便是逻辑思维和空间思维，这样才能够使学生在面对复杂的数学问题时快速理清解题思路.然而实际上，大多数初中生的数学思维能力普遍较弱，在面对抽象的数量关系和空间关系时，经常找不到问题的切入点，对解题思路毫无头绪，这也在一定程度上打击了学生学习数学的自信.而在解题教学中应用数形结合思想，能够引导学生从不同的层面去思考“数”和“形”的关键连接点，并找到正确的解题思路.这一思维方式使解题过程充满趣味性和探索性，当学生能够运用数形结合思想解开数学难题时，也会获得学习数学的乐趣与成就感，从而在潜移默化中提高自身的解题能力.

其次，增强数学解题思维的灵活性.在数学解题过程中应用数形结合思想主要有两个作用和方向：一是“以形辅数”，也就是用直观的图形关系辅助学生去理解抽象的数量关系，从而通过转变思维来开拓解题思路；二是“以数助形”，指的是用逻辑严谨的数量关系来表达抽象复杂的图形关系，从而降低解题难度.“数”与“形”的相互结合与转变使得数学解题思维更具灵活性和多变性，学生可以在初中数学解题过程中，利用数形结合思想灵活地解决数学问题，从不同的角度对不同类型的数学问题进行思考分析，并实现举一反三、一题多解.不仅如此，数形结合思想在提高学生解题效率的同时，还能够有效培养学生的逻辑思维能力，以及学生思考问题的灵活性和创新性.

1.3 初中数学数形结合思想的教学原则

若想在初中数学教学中有效地应用数形结合思想，教师需要遵循以下三个基本原则：

首先，要坚持等价应用原则.这意味着在应用数形结合思想时，需要确保代数与几何图形在转化过程中的等价性.无论是“数”转化为“形”，还是“形”转化为“数”，都要保证各自的性质和特征在转化过程中保持一致，这样才能确保数形结合思想在解决问题时的准确性和有效性.

其次，要坚持双向应用原则.教师既要利用图形的直观性来解决代数问题，也要利用代数的精确性来分析几何图形.通过这种双向应用的方式，学生可以更深入地理解数学问题的内在联系，提高他们解决数学问题的效率.同时，这也有助于培养学生全面分析问题的能力，增强学生的逻辑思维和空间想象能力.

最后，要坚持简单应用原则.在具体的问题解决过程中，教师要根据问题的性质选择合适的代数法或几何法，以简化问题解决的过程，提高解决问题的效率.这不仅可以降低学生解决问题的难度，也有助于增强学生的学习兴趣和自信心.

2 影响学生解题能力的原因

2.1 数学思想方法意识不强

解决数学问题离不开数学思想方法的支撑，尽管在初中阶段，教材中并未有一节课专门讲解数学思想方法，然而，从初一开始，每一本数学教材都在传递着各种各样的数学思想方法.这些数学思想方法隐藏在课本知识中，不易被直观地看到，相比数学知识的学习，数学思想方法的学习与运用要更为复杂和困难.许多学生的数学思想方法意识不强，主要原因在于：首先，一些学生审题后感觉有了解题思路后便快速开始解题，而解题思路也往往只有一种，没有用心去思考是否还有更多的解题方向，也没有思考哪种方法更适用于解题过程；其次，有些学生虽然对一些数学思想方法有所了解，但他们对这些方法的掌握往往停留在表面，不能理解各种思想方法的特性和使用范围，这就导致他们在面对具体问题时，无法灵活运用这些思想方法，或者在解决问题时出现失误.

2.2 數学思维能力较弱

《全日制义务教育数学课程标准（实验稿）》中提出：“……培养学生的演绎推理、总结归纳、构建模型、空间猜想等数学思维能力.”数学思维可以分为数学逻辑思维和数学形象思维，这两种思维既相互独立，又相互关联.一般来说，在解题过程中，学生首先通过审题来直观地理解题意，这就是形象思维的体现；之后，运用逻辑思维，对题意进行分析、推导和联想；最终将问题求解出来，这充分体现了逻辑思维的重要性.然而，在实际数学解题中，学生很容易受到定向思维的影响，当遇到常规或典型的例题时，他们能够根据所学的知识概念快速判断解题思路，但当面对开放探究型题目时，由于很多学生的思维能力较弱，思考问题时容易变得固化，不能灵活运用多种解题思维，导致解题受阻.

2.3 题后缺乏反思

在实际教学中，很多学生在发现解题错误后，只是简单地核对一下正确答案，并没有认真分析出错的原因，也没有反思解题思路和过程，没有真正地将错题搞明白，导致之后再遇到同样类型的问题时，仍然会再次出错，浪费了大量的時间和精力，解题能力也没有得到有效的提高.目前，许多学生都存在这样的问题，反复做题却反复出错，这是因为他们缺乏反思意识，不愿意主动去总结和分析错题，学生只是为了解题而解题，失去了解题的意义和价值.

3 数形结合思想在初中数学解题中的运用路径

3.1 运用数形结合思想解决不等式（组）的问题

不等式是初中数学学习中的基础知识，同时是初中数学知识结构中的重要一环.教师在日常教学中若用文字来简单描述不等式的内涵和概念，很难引发学生的深度思考，导致教学效果只流于表面形式.因此，在解决不等式问题的过程中，教师可以引导学生从数形结合思想的角度去发现解题思路，从而加深学生的学习效果.例如，关于x的不等式组0≤x²＋ax＋4≤2有唯一的解，求解a的值.由于题目中没有展示任何图形信息，很多学生在解题时便也不考虑用图形解题的思路，而是直接对题目进行计算.对于这类题目来说，运用数量分析的思路来解题并不是最优选择，不仅解题过程复杂而且还容易产生思路混淆.对此，教师可以引导学生运用数形结合思想对该不等式组进行拆解，得到y＝x²＋ax＋4，y＝0，y＝2这三个方程式，这时学生便想到可以通过图象绘制的方式来解题，并在此过程中找到三个方程式之间的关系，最终得出“只要抛物线和直线满足具有唯一交点这一条件，便能得到题目中所说的‘唯一的解”.通过这种解题方式，学生能够进一步了解到“图”与“形”之间切换和结合的关系，并在图象绘制的过程中使解题思路更加清晰，从而有效提高解题能力.

3.2 运用数形结合思想解决函数的问题

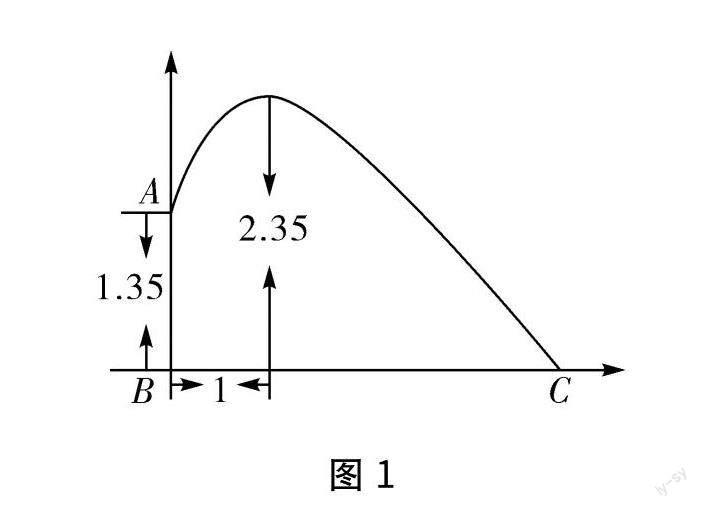
在实际解题过程中，很多学生对于复杂的函数问题往往无法快速理清思路，究其原因是因为学生没有找到空间关系与数量关系之间的连接点.函数问题实际上就是融入了代数知识以及几何内容的综合数学问题，因此在解决函数问题时，教师可以引导学生运用数形结合思想，通过“以形辅数”的思维快速找到解题的突破口.例如，小辉正在进行羽毛球训练，小辉的身高为1.35 m，高度以AB来表示，此时当他进行打击后，羽毛球击飞的最高点为2.35 m，若此时羽毛球与小辉的实际水平距离正好为1 m，则羽毛球的落点C和小辉的位置B的水平距离约多少米呢？通过图1能够看出，题目所求的B到C的距离是一条直线距离，其中涉及“抛物线”知识中的“应用型函数”这一知识点，通过观看图形和图象能够使学生快速地对该题有一个直观的了解.在运用数形结合思想分析时，教师要保证学生能够通过图象转换判断数量关系的准确性，并形成严谨的解题思路.

3.3 运用数形结合思想解决几何的问题

如果说不等式和函数问题都是通过数形结合思想中的“以形辅数”思维来解题的，那么几何问题则是通过“以数助形”的思维来解决的.几何问题就是基于几何定理，给出特定的条件和信息，通过分析得出最终结论，其难点主要在于学生即使了解所涉及的几何定理，但是也不能保证正确推理出证明过程.对此，就需要教师引导学生认真分析题目中所给出的条件和信息，将数量关系对应到空间关系，并且采用反向思维去推理验证，从而明晰解题思路.在实际解题时，很多学生会因为几何图形较为复杂而不知从何入手，这时教师可以指导学生将复杂烦琐的图形拆解成几个简单的图形，并从中找到有效信息，化繁为简，从而掌握分解图形的规律，并形成正确的解题思路.

例如，在几何证明中通过分析数字比值关系来证明三角形相似关系，通过运用数形结合思想能够有效合理地完成这一证明过程.如图2所示，四边形CBFG为正方形，且在△ACB中∠ABC＝90°，E为AG与CB的交点，D为AC上一点.已知AB∥DE，求证BE＝DE.

从图2中能够看出，BE与DE两条线段包含了两个三角形，因此教师可以引导学生将图形拆解为两个三角形，并通过图形中所给出的较多的平行条件作为解题方向，在证明BE＝DE时，可以通过比例线段进行推理和验证.具体步骤为：证明△ACG∽△ADE，则可以证明DE∶CG＝AE∶AG.证明△AEB∽△AGF，则可以证明BE∶FG＝AE∶AG，所以DE∶CG＝BE∶FG.同时因为在正方形CBFG中CG＝FG，所以BE＝DE.

4 结论

初中数学问题具有逻辑性和抽象性的特点，运用数形结合思想能够有效帮助学生明确解题方向，并且启发学生从多个角度去思考问题，拓展解题思维，从而做到举一反三.为了能够使学生更好地运用数形结合思想，教师需要制定出科学合理的教学计划，帮助学生构建完整的数学知识体系，及时做到题后反思，弥补知识漏洞，使学生养成良好的解题习惯和思维意识，从而真正有效地提高解题能力.

参考文献

［1］林勋. 初中数学渗透数形结合思想的策略［J］. 文理导航，2023（10）：67-69.

［2］徐尚花. 谈初中数学教学中数形结合思想的应用［J］. 试题与研究，2023（27）：156-157.

［3］罗志山. 利用数形结合思想巧思妙解几何问题［J］. 数理化解题研究，2023（26）：29-31.

［4］香钦源. 数形结合思想在初中数学解题中的应用［J］. 数理天地（初中版），2023（17）：20-21.

［5］辛艳，高丽. 初中数学教学中如何渗透数形结合思想［J］. 新智慧，2023（21）：80-82.

［6］赵银凤. 初中数学教学中渗透数形结合思想路径探析［J］. 学苑教育，2023（21）：57--58+61.

［7］王莹. 试析数形结合思想在初中数学解题中的应用［J］. 科学咨询，2022（7）： 185--187.

［8］谢为勤. 数形结合思想在初中数学教学中的应用探讨［J］. 亚太教育，2022（4）： 119--121.

［9］王美玲. 初中数学教学中数形结合思想的应用［J］. 吕梁教育学院学报，2020，37 （3）：101--102.

［10］谢艳平. 数形结合思想在初中数学教学中的应用［J］. 华夏教师，2020（21）：21--22.

［11］刘亚龙. 谈数形结合在初中数学教学中的应用［J］. 才智，2020（16）：219.