数形结合思想在初中数学反比例函数中的应用
2016-12-01曹小钢
曹小钢
摘 要:数形结合思想主要指的是将数学知识中的几何问题与代数问题结合起来考虑,既能发挥几何知识的直观性,又能发挥代数知识的严密性,充分地将两者的优势结合起来,从而帮助学生快速解决数学问题,并且在应用的过程中形成严密的逻辑思维,从而能够深入地了解数学的内在智慧,将数学知识融会贯通。将从具体的例题出发,简要谈谈数形结合思想在初中数学反比例函数中的应用。
关键词:数形结合思想;初中数学;反比例函数
恩格斯曾说过:“数学是研究现实世界的量的关系与空间形式的科学。”数形结合从某种意义上说,就是将数学问题之间的条件与结论进行一定的联系,将数学问题中的代数知识和几何知识运用、体现出来,将代数的准确性以及几何的直观性都充分地表现出来,将这些考虑问题的手段有效地结合在一起,从而促进数学解题思路的拓展与提升,从而将数学问题的难度降低,帮助学生更轻松、更直观地进行解题。反比例函数自身就是一种几何与代数知识的结合,因而在进行反比例函数解题的时候,我们应当尽量多地利用数形结合思想,将初中数学反比例函数中的问题更好地解决。
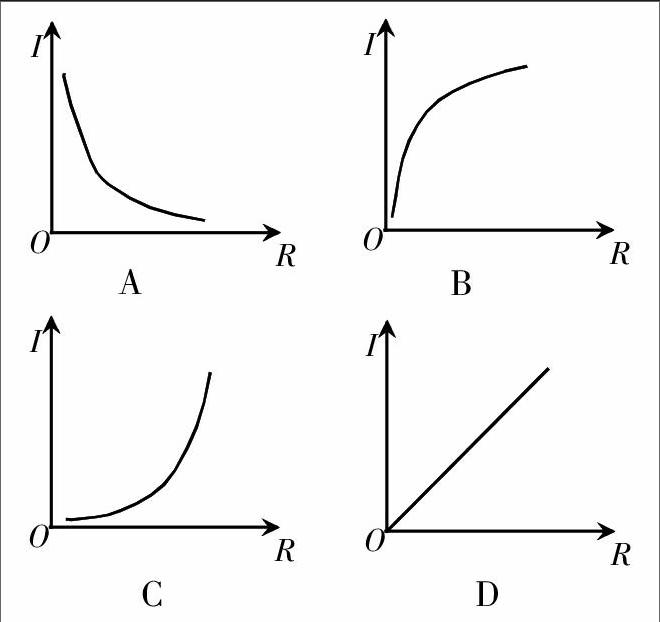
例1.已知圆柱的侧面积是20π cm2,若圆柱底面半径为r cm,高为h cm,则h关于r的函数图像大致是( )。
我们根据已知数据并且结合圆柱的侧面积表达公式即:s=2πrh,并且2πrh=20,那么我们就可以得到h=10/πr,因此我们可以知道π与r之间是反比例关系,在解决实际问题的时候,我们还应当关注题目的实际应用,即r作为半径应当有一个潜在的取值范围即r>0,那么我们就可以知道h与r之间的反比例函数关系图象一定是在第一象限,通过已有知识的掌握,联系现实实际,我们可以将问题答案成功地求出来。在这里,我们应用到的知识主要是反比例函数的定义,即,一般地,如果两个变量x、y之间的关系可以表示成y=k/x(k为常数,k≠0)的形式,那么称y是x的反比例函数。我们通过圆柱侧面积的表达公式,并将题目中已经掌握的信息利用起来,求出h与r之间的关系,发现与反比例函数的定义相符,那么我们就可以判定这肯定是一个反比例函数图象,接着,我们就可以确定答案为A。当然,这道题目中的解题思考进行概括和升华之后可以是这样的:我们在进行解题时,应当先找出两个变量之间的关系,根据这个关系式我们可以画出相应的函数图象,从而能够归纳出相应的图象特征,并找到相应的函数图像。
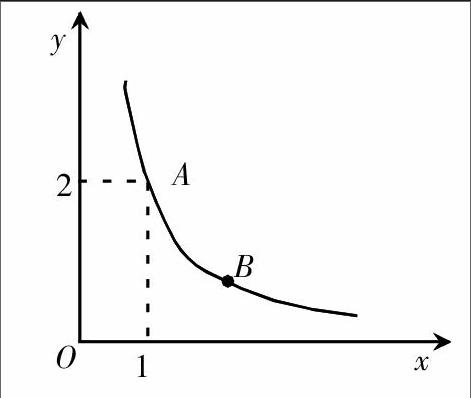
例2.如图:A、B是双曲线一个分支上的两点,且B(a,b)在点A的右侧,则b的取值范围是—( )。
根据题目中的图像所示,我们可以得出A点的坐标为(1,2),同时我们知道B点也是这个双曲线一个分支上的一点,因此点B的坐标可以利用双曲线的函数关系式表达成为(a,2a),又因为点B位于点A的右侧,那么我们可以根据反比例函数图象在第一象限中的变化规律得出y随着x的增大而减少的结果,因此我们可以得出a一定大于1,且b一定小于2,b一定大于0,也就是b大于0且b小于2。在这道题目的解题过程中,我们主要运用的解题思路是结合我们已知的条件,从图象中寻找有用的相关信息,从而能够将已知条件转化为要求的目标,只有充分地结合图像,我们才能将所有的条件都考虑完整,不会将“b在第一象限,所以一定大于0”的信息给忽略掉,从而得出更为准确的答案。
总而言之,反比例函数作为一种重要且有效的数学解题手段,我们应当帮助学生在数学思维养成的过程中逐步学会这种思维手段,并将其熟练地运用到数学解题过程中去。对于反比例函数中比较突出的问题,包括比较大小、通过应用题目确定数值关系式等,我们应当运用数形结合的解题思想进行解题,从而达到事半功倍的解题效果,实现反比例函数的优质解题。
参考文献:
[1]李浩明.数形结合在反比例函数中的应用[J].语数外学习,2008(6).
[2]雷祥红.与反比例函数大小有关的大小比较:感悟数形结合思想的应用[J].中学课程辅导,2007(2).
