指向推理能力的核心问题设计

钱筱珍 陈碧芬

【摘  要】  推理是数学严谨性的基础，也是发现数学结论、构建数学体系与交流的重要方式.探究指向推理能力的核心问题设计流程——培养目标确定、核心问题选择、核心问题设计、子问题链设计和核心问题改进，以期在探究核心问题的过程中培养学生的推理能力.

【关键词】  推理能力；核心问题设计；初中数学

《义务教育数学课程标准（2022年版）》指出：数学教育应使初中生达到“三会”的境界，其中包括会用数学的思维思考现实世界［1］. 在这方面，学生推理意识和推理能力的培养至关重要. 然而，学生的推理能力不甚理想，在实际教学中教师也常由于缺乏切实可行的培养方法而停留在知识的传授上. 因此，培养推理能力无疑是中学教学中的一大重点和挑战. 问题能促进学习思考，核心问题作为一节课中最关键、具有启发性和挑战性的中心问题，能促进学生思考，有效落实数学核心素养. 本文旨在探讨如何设计指向推理能力的核心问题，并以浙教版“完全平方公式”为例进行具体阐述. 1  指向推理能力的核心问题设计

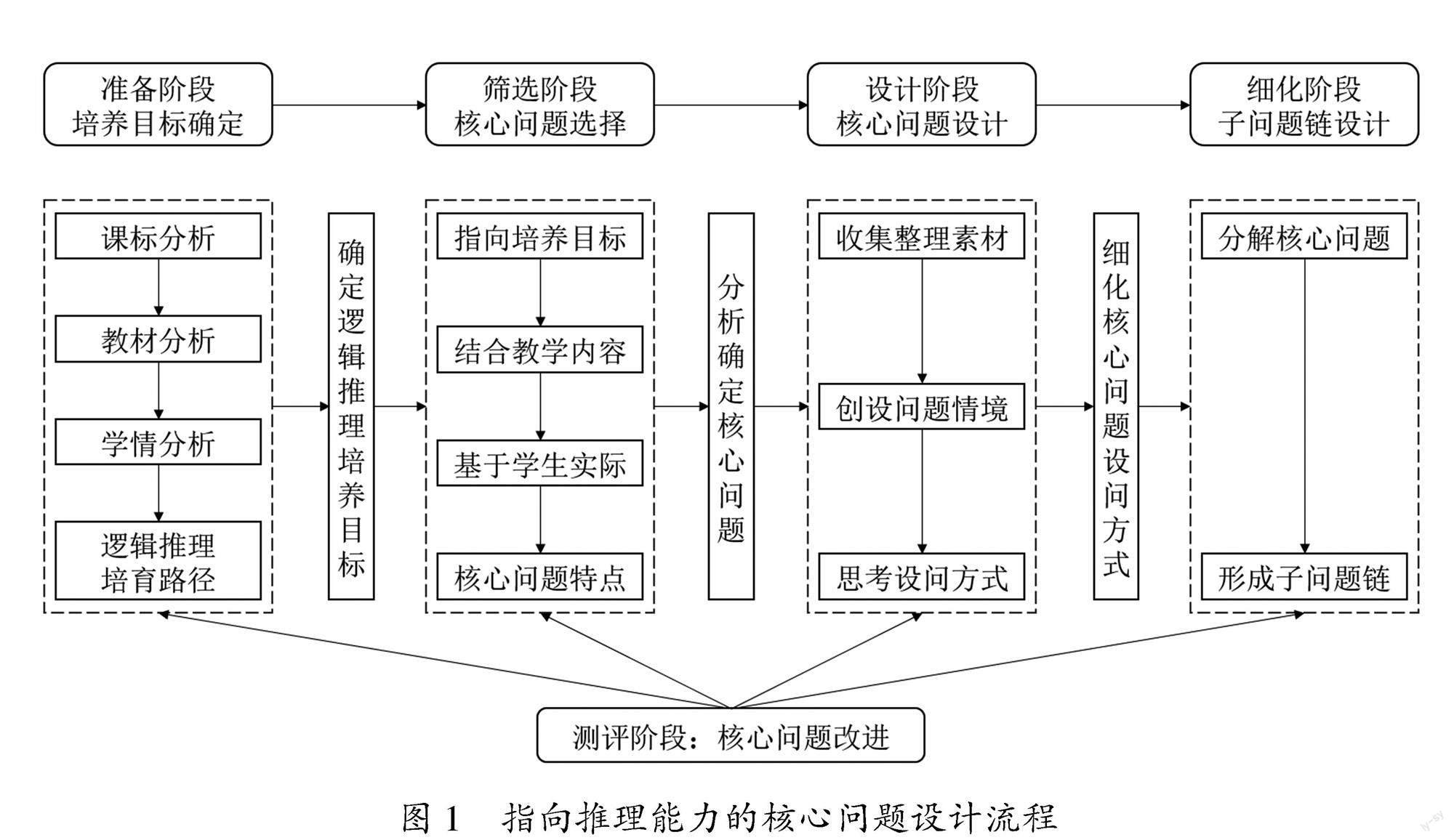
指向推理能力的核心问题是指针对教学内容的整体性和学生的认知水平提炼出的中心问题，是在诸多问题中最具思维价值且最能揭示知识本质的关键性问题.这些问题有一定的思维深度，能够激发学生的问题意识和主动参与，旨在引导学生进行逻辑思考和推理，帮助他们理解知识的本质，推动他们在推理能力方面的学习和发展.和一般的核心问题相比，指向推理能力的核心问题主要有以下特征：整体性和深刻性，逻辑性和严谨性，以及开放性和创新性.整体性和深刻性强调知识之间的相互关联和思考问题的深度，逻辑性和严谨性注重问题间的逻辑脉络和推理过程的严谨性，开放性和创新性则重在激发学生的探索欲望和创新能力.基于上述特点并结合郭妍提出的逻辑推理的培育路径［2］，构建指向推理能力的核心问题设计流程，包括培养目标确定、核心问题选择、核心问题设计、子问题链设计和核心问题改进这五个环节（如图1）.

首先在准备阶段，依据课标、教材、学情和逻辑推理培育路径，确定学生推理能力的具体培养目标. 其次在筛选阶段，根据所确定的培养目标整合学习问题，生成一个或多个具有统摄作用且指向推理能力培养的核心问题，并用简练术语表示出来. 在设计阶段对所选问题进行深入分析. 在这个阶段，教师需要进一步了解问题的背景和相关概念，确定学生在解决问题时可能遇到的难点及关键要素，收集相关问题情境素材，结合培养目标思考核心问题具体、清晰的设问方式，使学生能够理解和回答. 随后在细化阶段，教师需要将核心问题进一步分解为一系列有序的子问题. 每个子问题都应该与核心问题紧密相关，并且能够引导学生思考和推理，最终解决核心问题. 注意，子问题链的设计应该具有逻辑性和连贯性，确保学生在解决问题的过程中逐步积累知识和提升推理能力. 最后，测评环节贯穿在每一个阶段当中，教师可以使用不同的评估方法来验证问题的有效性，如教师观察、学生表现评价、小组讨论和作品展示等，并根据评估结果对核心问题和子问题链进行改进和优化，以更好地促进学生的推理能力的培养.

2  教学案例

下面以浙教版“完全平方公式”为例，具体阐述如何根据上文所构建的设计流程设计核心问题.

2.1  准备阶段：培养目标确定

课标分析  课标中对完全平方公式的要求为“理解完全平方公式，了解完全平方公式的几何背景，能利用公式进行简单的计算和推理”［1］. 立足所选课题，可以将其理解为以下三个方面：第一，学生需要理解完全平方公式的含义、原理和应用. 通过深入理解完全平方公式的含义和原理，学生可以更好地掌握它的应用，提高数学抽象能力. 第二，学生需要了解完全平方公式与几何图形之间的关系. 这有助于学生更好地理解完全平方公式，明白平方项的含义以及乘积项的来源. 同时，通过这种几何视觉化的方式，学生可以更直观地理解完全平方公式的运用和推导过程. 第三，学生需要掌握利用完全平方公式进行计算和推理的能力. 这包括根据给定的数值计算出完全平方形式的结果，能够通过完全平方公式推导出其他相关的数学表达式，以及能够在实际问题中应用该公式.

教材分析  本课时内容是在整式的乘法以及平方差公式的基础上，进一步研究多项式与多项式的乘法公式，是前面所学知识的应用和发展. 同时，完全平方公式是后续学习因式分解、配方法等知识的基础，因此本节课起着承上启下的作用. 教材从多项式的乘法（数）和图形面积割补（形）两个角度得到完全平方公式，再通过例、习题教学帮助学生理解公式，有利于培养学生严谨的推理能力和钻研精神. 结合以上分析，确定本节课的教学重点：完全平方公式的推导和应用.

学情分析  在本节课之前，学生经历了数与式的承接，初步实现了从算术思维到代数思维的转变，完成了幂的运算、整式的乘法和平方差公式等知识的学习，能够运用整式相关法则进行计算，并能通过合并同类项进行化简. 同时在学习多项式乘法和平方差公式的过程中体验了如何用圖形的面积关系来说明多项式乘法的法则，有了初步的数形结合意识，具备了一定的数学活动经验. 但学生的逻辑思维还不够严谨，对数学的认识还不够深刻：其一，公式中的字母a，b本身具有广泛性，尤其是字母a，b是带有数字系数的单项式时，学生容易忽略公式中字母的结构特征以及含义；其二，从两数和的完全平方公式到两数差的完全平方公式要用到换元思想，对学生来说也是一难点. 结合以上分析，确定本节课的教学难点是公式中字母的含义，从两数和的完全平方公式到两数差的完全平方公式的推理方法.

培养目标确定  “完全平方公式”培养目标，见表1.

2.2  筛选阶段：核心问题选择

结合培养目标，从五个层次分别初步确定对应的五个核心问题，如表2.

2.3  设计阶段：核心问题设计+细化阶段——子问题链设计

根据培养目标和初步确定的核心问题设计具体核心问题及子问题链，并形成完整的教学设计.

核心问题1  如何利用多项式与多项式的乘法法则推出完全平方公式？

子问题1：多项式与多项式乘法的法则是什么？如何用字母表示？如何用几何图形反映？

子问题2：上述四个长方形中，其中一个演变成正方形，即x=y时，整式的乘法公式如何演变？

追问：结合上述公式，根据以下条件分别求出（x+p）（x+q）的值，并观察所给p，q的值.

（1）p=1，q=－1；  （2）p=23，q=－23；

（3）p=－3m，q=3m；  （4）p=－12n，q=12n.

子问题3：p，q互为相反数是一种特殊情形，当p=q呢［3］？又会出现怎样的情形.

设计意图  从整体视角出发，以多项式的乘法公式为切入点，将平方差公式和完全平方公式巧妙地融入整式乘法的大体系中，体现它们之间的密切联系：平方差公式和完全平方公式都是整式乘法中最特殊的两类情况（p，q相等或相反）.这樣，学生可以更好地理解整个章节知识的连贯性与联系性.

核心问题2  利用两数和的完全平方公式解决其它多项式乘法.

子问题1：用两数和的完全平方公式计算（填空）.

（1）（a+1）2=（  ）2+2（  ）（  ）+（  ）2=;

（2）（2a+3b）2=（  ）2+2（  ）（  ）+（  ）2=.

追问：两数和的完全平方公式中的字母表示什么含义？

子问题2：利用两数和的完全平方公式计算（a-b）2=？

设计意图  一方面让学生深入理解完全平方公式中字母的多重含义，另一方面引导学生利用换元思想从两数和的完全平方公式推出两数差的完全平方公式，让学生体悟代数推理的过程与思想.

核心问题3  为什么要引入完全平方公式，它解决了什么样的数学问题？

子问题1：利用完全平方公式计算：

（1）（x+2y）2;（2）（2a－5）2;（3）（－2s+t）2

（4）（－3x－4y）2;（5）992;（6）1032

子问题2：一花农有2块正方形茶花苗圃，边长分别为30.1m，29.5m，现将这2块苗圃的边长都增加1.5m后，求各苗圃的面积分别增加了多少m2？

设计意图  子问题1前4小题是让学生立足完全平方公式运用整体思想解决问题，后两道计算题是让学生运用转化思想，达到简化计算的目的.子问题2是现实问题，让学生体会完全平方公式的实际应用.

核心问题4  多项式的乘法公式有其几何背景，这两个完全平方公式能否也用几何图形进行验证呢？

探究1：用图2的四张卡片摆出一个大正方形，要求：图形之间不能有重叠、不能有空隙.图2  探究1对应卡片

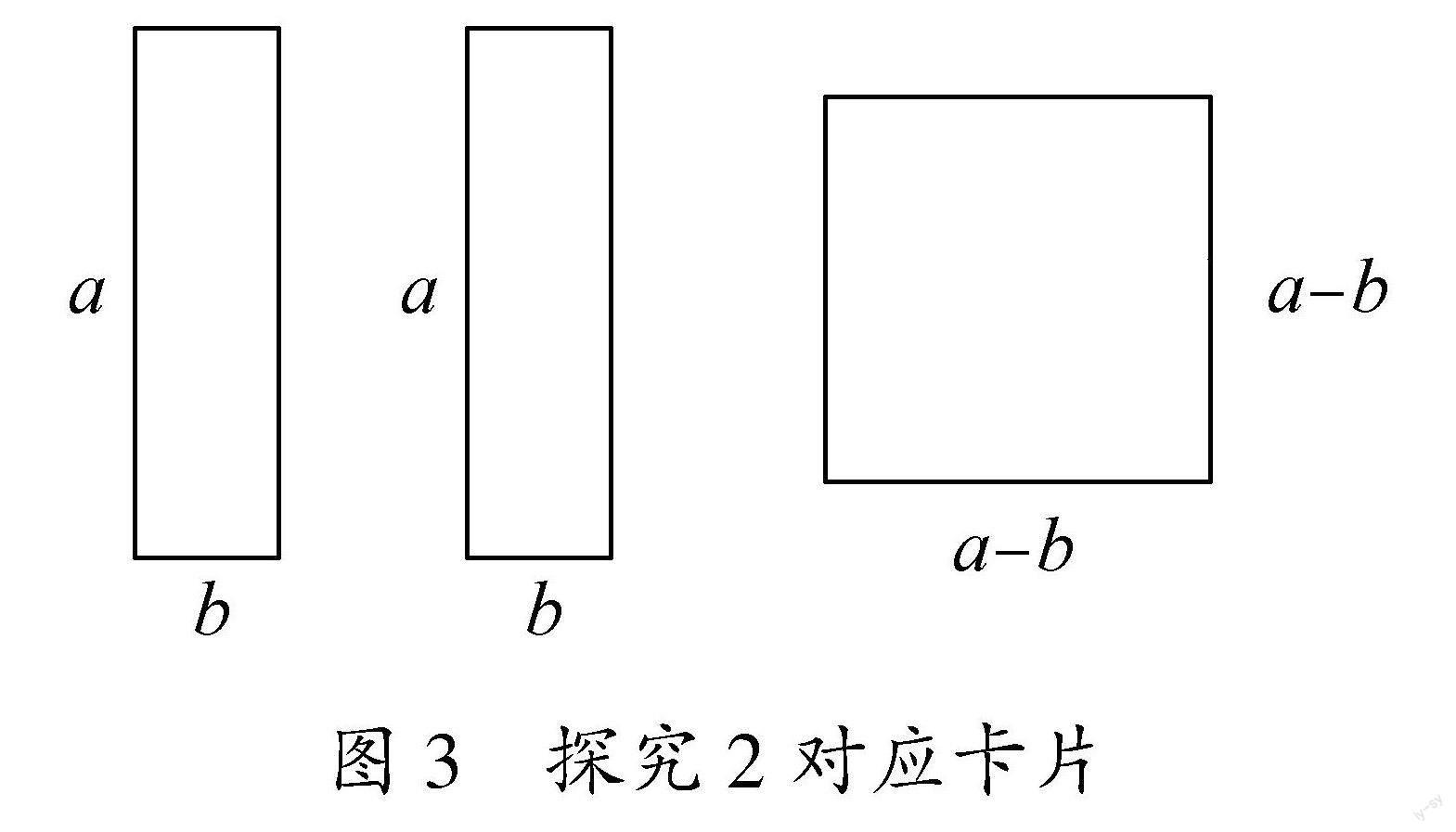
探究2：用图3的三张卡片摆出一个大正方形，要求：图形之间允许有重叠.图3  探究2对应卡片

设计意图  从图形面积割补两个角度再次验证完全平方公式，在探究的过程中理解完全平方公式的几何意义，体会数形结合思想，提升学生直观想象素养.

核心问题5  梳理完全平方公式的推导过程、总结思想方法.

子问题1：本节课学习完全平方公式的路径是怎样的？在这探究过程中体现了哪些数学方法.

设计意图  让学生梳理完全平方公式的学习路径，以促进学生深入理解和掌握完全平方公式.此外，通过回顾思想方法，凝练问题解决的一般路径，旨在培养学生解题的基本思路，并提升其问题解决能力.

3  教学反思

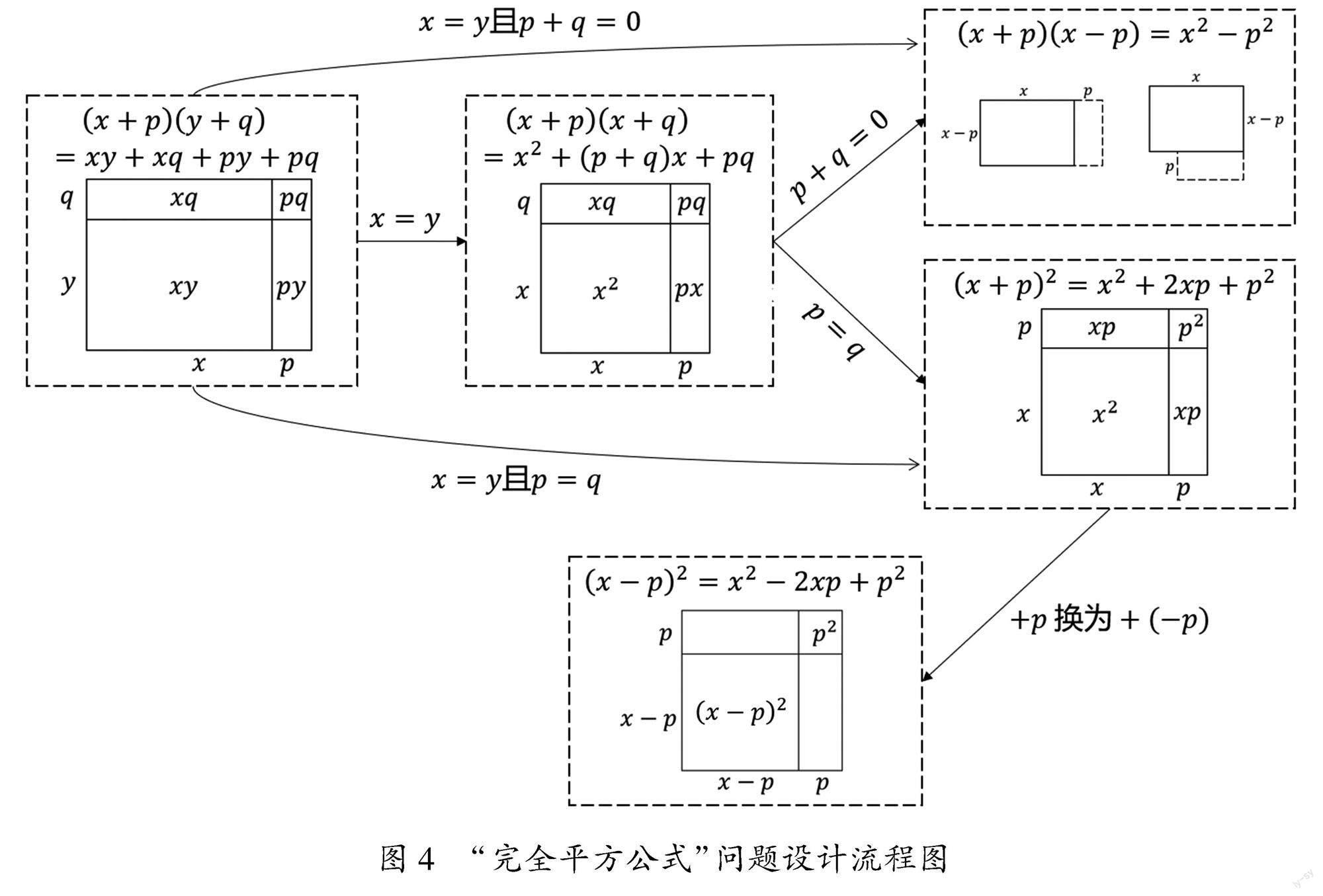
数学的结构化特征决定了各课时内容之间也并非完全独立的.因此，在设计核心问题时应从整体上分析新旧知识之间的关系. 上述指向推理能力的核心问题设计流程从多方面考虑确定培养目标，催生出核心问题，接着形成具有逻辑关联性的子问题串，清晰地揭示了数学内容之间的联系. 在案例中，问题设计也注重整体性策略，以“数”为主、“形”为辅，主要的问题设计流程图如图4. 以多项式的乘法作为起点，将“多项式乘法法则”“平方差公式”和“完全平方公式”联系起来，同时结合长方形面积的变化，将数学与几何图形相结合，有效地整合了各个内容之间的逻辑结构. 这样，同根同源的平方差公式和完全平方公式就能够作为一个整体呈现，使学生见“树”还见“林”. 通过核心问题引导学生用全局的视角和系统的思维去构建知识体系，这对于学生理解知识、实现对知识的整体建构以及提升学生的推理能力都大有裨益.

参考文献

［1］中华人民共和国教育部.义务教育数学课程标准［M］.北京：北京师范大学出版社，2022：6.

［2］郭妍，沈建民.高中数学逻辑推理素养的生成价值与培育路径［J］.教学与管理，2023（03）：94-97.

［3］冯俊.教材整合建构  强化思维训练——大单元教学背景下“完全平方公式”的教学设计［J］.初中数学教与学，2021（16）：27-29.

作者简介  钱筱珍（1998—），女，浙江杭州人，硕士研究生；从事数学课程与教学研究.

陈碧芬（1979—），女，浙江奉化人，博士，副教授，硕士生导师；主要从事数学课程与教学研究.