把握图形结构 激活数学思维

基金项目  聊城市重大攻关科研课题“教育信息化下的教师专业发展研究”（LJZ16015）.

【摘  要】  以2023年北京中考卷第27题为例，通过把握图形特征，分析图形性质，借助图形分析问题，探索解决问题的思路，分析问题情境中的基本图形，探究其中的不变关系，达成高效解题，体现试题的育人价值.

【关键词】  关注整体；基本图形；几何直观；学科素养

1  试题呈现

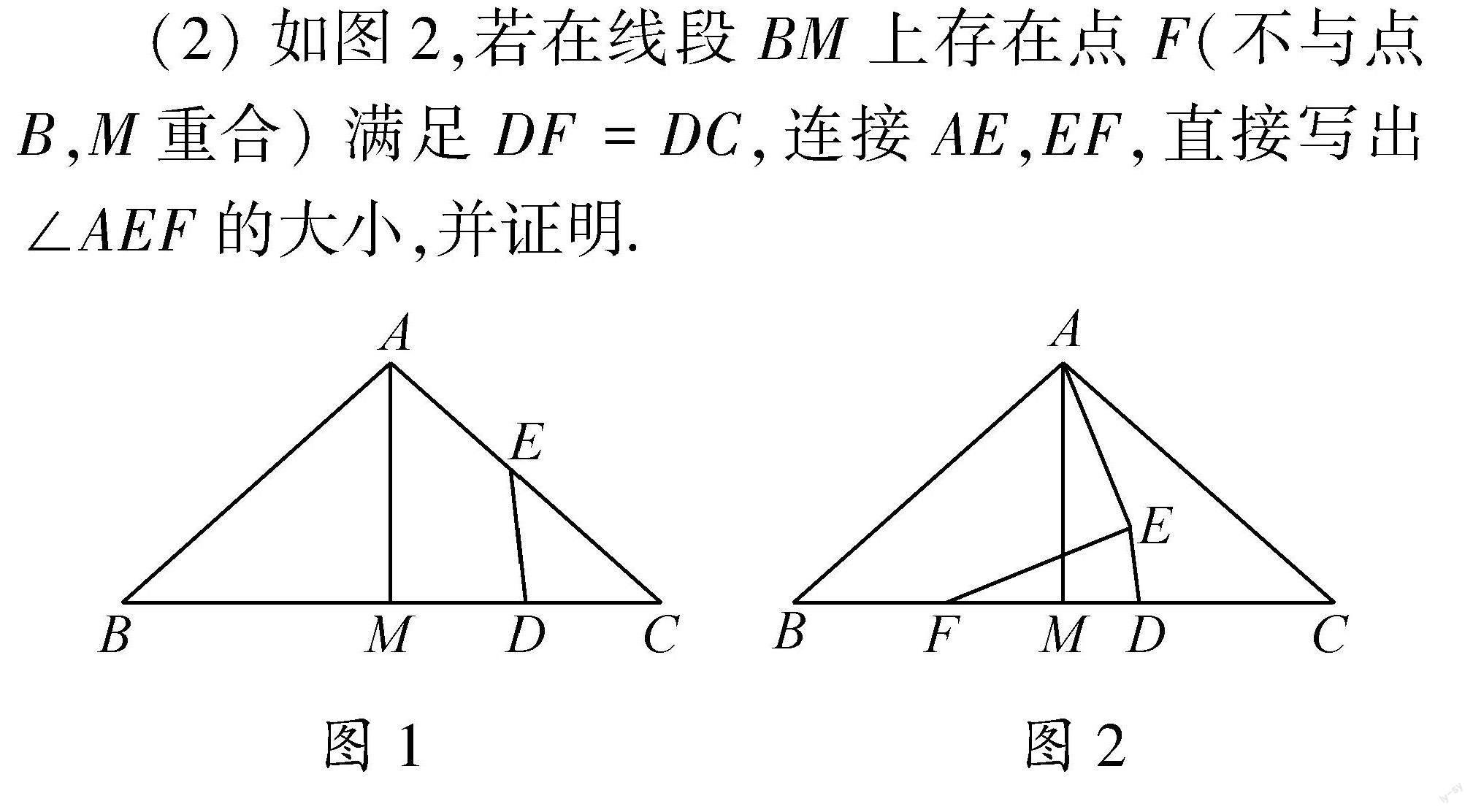
题目  在△ABC中，∠B＝∠C＝α（0°＜α＜45°），AM⊥BC于点M，D是线段MC上的动点（不与点M，C重合），将线段DM绕点D顺时针旋转2α得到线段DE．

（1）如图1，当点E在线段AC上时，求证：D是MC的中点；

（2）如图2，若在线段BM上存在点F（不与点B，M重合）满足DF＝DC，连接AE，EF，直接写出∠AEF的大小，并证明．

图1          图2

2  试题分析

本题是一道几何综合题，主要考查“图形与几何”知识领域的相关内容，考查学生是否理解图形运动的变化特征，发现其中蕴含的不变关系，能否运用几何图形的基本性质进行推理论证.考查学生是否具备一定的几何直观、空间观念和推理能力.

解题思路一定要从题目条件出发，顺藤摸瓜，分析每个条件背后的含义，将可能推导出的结论连接成知识网络.线段、角的计算、证明基本都是利用三角形全等、相似，直角三角形性质、三角函数等知识点进行考查的［1］.第（1）问，主要考查对线段旋转这一概念的理解与运用，三角形的外角性质的运用、等腰三角形的判定，难度不大.

难度主要集中在第（2）问.当点D在线段MC上运动（不与M，C重合）时，始终有DM=DE，DF=DC，∠FDE=2α，图1中的点M就可以看作点F的特殊位置，连接EM（如图3），则ED=FD=CD，从而E，M，C在以D为圆心，MC为直径的圆上，从而根据“直径所对的圆周角是直角”，可得∠MEC=90°，所以∠AEF=90°.关注特殊位置，可以让我们快速确定定值［2］.这样的特殊位置还可以是图4、图5.图6是借助几何画板验证点D在线段MC上运动，∠AEF的运动轨迹，借助其度量功能，∠AEF的大小始终不变，为90°.图3          3  解法探究

解法1  如图7，延长DE，交AC于T，连接FT，则FD=DT=DC，根据“一边中线等于这边一半的三角形是直角三角形”或者圆的定义结合圆周角定理推论，可得∠FTC=90°，所以∠FTA=90°，又因为∠FMA=90°，取AF中点O，连接OT，OM，根据“直角三角形斜边中线等于斜边一半”，可得OT=OA=OF=OM，根据圆的定义，可得A，F，M，T在⊙O上，且AF为⊙O直径，由DE=DM，DF=DT，可得∠DEM=∠DFT=180°-∠MDE2，根据“外角等于它的内对角的四边形四个顶点在同一个圆上”，可得F，M，T，E在同一个圆上，然后根据“经过不在同一直线上的三点有且只有一个圆”，故E在⊙O上，又因为AF为⊙O直径，所以∠AEF=90°.

点评  解法1着眼整体，注重与第（1）问的关联，充分利用圆的定义，确定圆的条件，以及确定四点共圆的条件，圆周角定理的推论等，来确定思路.当F在线段CM上时，如图8，仍然可以用这种思路.从解法1中发现：第一，∠AFE=∠AME=α始终成立；第二，通过证明△OFM≌△OTE，得到OE=OM说明E在⊙O上.这样更易理解.

解法2  如图9，延长FE到N，使EN=FE，连接AF，AN，CN，由EF=EN，DF=DC，可得DE为△FCN的中位线，根据“三角形的中位线平行于第三边，且等于第三边的一半”，可得DE∥CN，DE=12CN.因为AB=AC，AM⊥BC，所以BM=CM=12BC，又因为DF=DC=12CF，所以DE=DM=CM-CD=12BC-12CF=12BF，所以CN=BF.因为DE∥CN，所以∠NCD=∠EDM=2α，又因为∠B=∠ACB=α，所以∠ACN=∠B.在△ABF和△CAN中，因為AB=AC，∠B=∠ACN，BF=CN，所以△ABF≌△CAN（SAS），所以AF=AN，又因为EN=FE，所以根据等腰三角形“三线合一”的性质，可得AE⊥FN，从而∠AEF=90°.

点评  当F在线段CM上时，如图10，仍然可以用这种思路.寻求线段间的数量关系，对几何图形的定性定量分析，往往至关重要.在几何学习过程中，线段的中点是常见的条件之一，当图形中有中点时，要注意联系“三角形中线”“直角三角形斜边中线”“等腰三角形底边中线”“三角形中位线”等知识，合理添加辅助线，构造有关基本图形.发现DM是BF的一半（还可以用代数法来推导，可以设BM=CM=x，DF=DC=y，则DM=x-y，而BF=2x-2y），是证明三角形全等的关键，史宁中教授指出：越是直观的越难抽象［3］.在学习过程中，两个共顶点且顶角相等的等腰三角形形成的全等三角形较为常见［4］.如果先绕点A逆时针旋转△ABF到△ACN处，再连接FN，需要证明△FDE∽△FCN，得到∠DFE=∠DFN，结合两角相等的定义（叠合法）来说明另一边FE，FN也重合，从而说明F，E，N三点在同一直线上，下同解法2.

解法3  如图11，连接AF，并取其中点O，连接OM，OD，OE，因为OF=OA，DF=DC，所以OD为△FAC的中位线，所以OD∥AC，∠ODM=∠C=α，又因为∠MDE=2α，所以∠ODE=∠ODM=α，在△OMD和△OED中，因为MD=ED，∠ODM=∠ODE，OD=OD，所以△OMD≌△OED，所以OE=OM=OA=OF，根据圆的定义结合圆周角定理推论或“一边中线等于这边一半的三角形是直角三角形”，可得∠AEF=90°.

点评  如图12，当点F在线段CM上时，仍然可以用三角形全等这种思路，当然在图11、图12中，如果连接ME，由DM=DE，DO平分∠MDE，得DO垂直平分ME，那么OE=OM，利用这种思路也是可以的.我们在得到OE=OA=OF后，除了利用“圆的定义结合圆周角定理推论”或“一边中线等于这边一半的三角形是直角三角形”外，利用∠AEF=∠AEO+∠FEO=180°-∠AOE2+180°-∠FOE2，来得到∠AEF=90°也是可以的.

解法4  如图13，连接ME，作EG∥AC，交BC于G.则∠EGM=∠C=α，MD=ED=DG，∠MEG=90°，由DM=DG，DF=DC，得DF+DG=DC+DM，即FG=CM，从而tanα=EMEG=AMCM=AMFG，由∠AME+∠EMG=90°，∠FGE+∠EMG=90°，得∠AME=∠FGE，根据“两边成比例且夹角相等的两个三角形相似”，得△AME∽△FGE，所以∠AEM=∠FEG，从而∠AEF=∠MEG=90°.

点评  如图14，当点F在线段CM上时，仍然可以用解法4这种思路.在解法4中，得到FG=CM是问题解决的关键.

解法5  如图15，记EF交AM于K，作DN∥AC，交AM于N，连接EN.则∠MDN=∠C=α，则∠NDE=∠MDE-∠MDN=α=∠MDN，且MD=ED，ND是公共边，所以△NMD≌△NED，所以NE=NM，∠NED=∠NMD=90°，根据“四边形内角和等于360°”，可得∠MNE，∠MDE互补，又因为∠MNE，∠ANE互补，所以∠ANE=∠FDE.ANFD=ANCD=MNMD=NEDE，所以△ANE∽△FDE，所以∠NAE=∠DFE，又∠AKE=∠FKM，所以∠AEF=∠AMB=90°.

点评  如图16，当点F在线段CM上时，仍然可以用解法5这种思路.结合解法2和解法4，继续思考，可以得到解法6、解法7.

解法6  如图17，连接AF，ME，作DH⊥ME，垂足为H.因为DM=DE，DH⊥ME，所以∠MDH=12∠MDE=α，MH=12ME，由解法2，知DM=12BF，AMAB=sinα=MHDM=12ME12BF=MEBF，由解法4，知∠AME=α=∠B，所以△AME∽△ABF，所以ABAM=AFAE，∠BAF=∠MAE，从而ABAF=AMAE，∠BAM=∠FAE，所以△ABM∽△AFE，所以∠AEF=∠AMB=90°.当F在CM上时（如图18），结论∠AEF=90°仍然成立.

解法7  如图19，记FE交AM于K，连接ME，CE，延长ED到N，使DN=ED，连接FN，MN，CN，由DF=DC，DN=ED，根据“对角线互相平分的四边形是平行四边形”，可得四边形CEFN为平行四边形，所以FE∥CN，所以∠KFM=∠MCN，由MD=DE=DN，∠MDE=2α，得∠EMN=90°，∠MNE=α，所以MEMN=tanα=AMCM，由∠AMC=∠EMN=90°，得∠AME=∠CMN，所以△AME∽△CMN，所以∠MAE=∠MCN，所以∠MAE=∠KFM，又因为∠AKE=∠FKM，所以∠AEF=∠KMF=90°.用这种方法仍可证明点F在线段CM上时（如图20），∠AEF=90°.

点评  当然还可以不连接FN，倍长ED，得到△FDE≌△CDN，利用△AMC∽△EMN或由∠ACM=∠ENM得两角正切值相等，即AMCM=MEMN，下同解法7也是可以的.一般地，在图形中遇到一个中点时，可倍长中线，补成一个中心对称图形，达到转移线段位置的目的.进一步分析，如图21，在△ABC中，∠B＝∠C＝α（0°＜α＜45°），AM⊥BC于点M，动点D在BC的延长线上时，动点F在线段CD的延长线上，DF=DC，将线段DM绕点D顺时针旋转2α得到线段DE．∠AEF=90°仍然成立.

4  教学启示

对知识掌握的灵活程度决定着知识的应用层级，从模仿套用→分析整理→融合创新，体现了知识运用的三个层次.完整的知识体系和方法体系只是第一步，针对不同的问题总结归纳图形结构，联想有关基本图形，抽象图形的性质，及有效应对方法是第二步，熟练灵活的选用恰当的方法是第三步.在几何教学中，引导学生理解图形构造，显得极为重要.4.1  领悟联结学习，把握教学价值取向

教育学家桑代克指出：学习的实质是在一定的情境和一定的反应之间建立联结［5］.本题在命题结构上有所创新，试题引导学生通过画图、观察和分析图形运动变化的全过程，猜想、探究其中的不变关系，思考并证明自己的猜想，考查学生直观想象、逻辑推理等数学素养和从特殊到一般的数學思维价值方法.图形结构较为简单，一个等腰三角形，一个动点，赋予旋转和中点意义之后，整个图形就活了，既能构造旋转全等或相似，也可以构造中位线，并且相互关联得到更多新的结论，其中丰富的直角三角形，除了用于“导角”之外，还可以借助斜边上的中线，以及寻找共斜边的直角三角形，发现隐圆，从而由直线型跳到圆弧型进行构图.4.2  把握图形结构，有效提高解题能力

立足整体把握，帮助学生寻求基于问题情境、深挖背景知识的自然解法.最佳解法是解题教学的基本要求.把复杂的几何图形转化为简单的基本图形，或者把简约且内涵丰富的图形丰富完善，是数学转化思想的体现.通过一题多解，能有效触发学生多角度，多方位的思考，促进知识向学科素养的转化；全面联动相关知识，促进数学知识体系的有效建构.学无止境，注重知识的形成过程与解后的反思与回顾，积累成功经验，知其然，知其所以然，建立学生与知识的意义联系，方能真正落实能力与素养的培养［6］.基本图形在几何解题教学中，有着重要作用［7］.我们在数学教学中应帮助学生养成画图的习惯，建立分离基本图形的能力.回顾本题的解法，解法1通过圆的定义结合三角形全等，解法2、解法3构造三角形全等，解法4—7，分别以E，A，M为顶点，构造共顶点相似三角形，通过“组形→补形→变形”，使学生感知运用基本图形进行思考，注重“画图、读图、析图”能力的培养，总结基本图形的特征.既要能拓展基本图形的变化，也要能在复杂几何图形中完成构造、提炼基本图形，实现多图相关，寻找解决问题的突破口.借助几何直观和空间想象构建几何问题的数学模型，对问题进行探索并促进逻辑推理的锻炼与养成，感受数学思想方法的魅力.随着多方位知识的调用与重组，又促进了思维的不断创新，创新意识就在把握数学知识的本质、联系的过程中逐渐形成.4.3  整体把握教学内容，强化联结，优化数学教学

基于中考试题开展解题研究和教学实践，是数学教师的基本教学任务，也是提高学生解题能力的基本途径［6］.平时解题训练不应只求做对，而应力求把问题做透.只有把问题理解透彻了，我们才能真正透過现象捕捉到问题（图形）本质，才算达到做透的境界，小题要做出深度，大题要做出广度.逻辑结构是数学问题的核心，从条件到结论或者从结论到条件都有其内在的联系.要想弄清问题的结构关系，就要进退有序，顺势而为，则思路畅通，盘活全局.在当前“双减”时代背景下，引领学生从学会走向会学是重要目标，在数学教学中，不仅要注重具体内容与核心素养的关联，还要注重内容的主线与核心素养发展之间的关联［8］.优秀的中考试题就像一个有多个入口和出口的迷宫，且每条路一眼看不到头，需要我们不断尝试，不断强化联结，找到适合的路径.郭华教授指出：学习的过程，不仅仅是学习知识，不止于学习知识，要把教学内容转化为学生的精神力量［9］.在教学中要注意“教学内容的逻辑”“学生心理的逻辑”有机结合［10］，教学设计要体现“教学内容的本质”“在学生思维的最近发展区”“关注通性通法”“关注问题的发展性”的原则.数学教学的过程要缓渗透，勤反思，多质疑，在课堂教学过程中，关注学生的思维起点和对问题的结构分析，促进学习真正发生，让核心素养真正落地.

参考文献

［1］齐欣.例析线段、角的计算与证明［J］.数理化学习（初中版），2017（02）：7-10.

［2］齐欣.关注特殊位置，快速求解定值［J］.数理化学习（初中版），2017（10）：24-25.

［3］史宁中.数学思想概论（第2辑）——图形与图形关系的抽象［M］.长春：东北师范大学出版社，2009.

［4］齐欣.2022年苏州中考数学试题第8题解法研究［J］.数理化学习（初中版），2023（05）：6-9.

［5］张大均.教育心理学 ［M］.第3版.北京：人民教育出版社，2015.

［6］郑振兴.注重研形求理，达成解题高效——一道中考试题的评价、解法赏析和教学启示［J］.中国数学教育（初中版），2023（06）：55-58.

［7］周斌.一题多解拓思维基本图形显魅力［J］.中小学数学（初中版），2021（03）：31-32.

［8］中华人民共和国教育部.义务教育数学课程标准（2022年版）［M］.北京：北京师范大学出版社，2022.

［9］郭华.教学的模样［M］.北京：教育科学出版社，2022.

［10］金钟植.“数学通性通法”的研究综述及其现实意义［J］.数学通报，2021（01）：32-38.

作者简介  齐欣（1976—），男，山东临清人，中学高级教师；主要从事初中数学教育研究.