直角三角形内接定形直角三角形的面积最值
2024-01-22邓文忠



【摘 要】 解最值题的一般策略是动静转化,以静制动,捕捉特殊瞬间,凸显问题本质.从学生易接受的二次函数法和几何法角度对直角三角形内接定形直角三角形的面积最值予以探究,丰富了解法.
【关键词】 直角三角形;内接;三角形面积最值;二次函数法;几何法
1 问题呈现及缘由
△ABC中,∠C=90°,BC=a,AC=b,AB=c,D,E,F分别是AB,AC,BC上的点.若△DEF是两直角边DE与DF之比为定值λ(λ为正常数)的直角三角形,探究△DEF面积的最值.
文[1]利用三角法得到了直角三角形的任意内接直角三角形面积的最小值,并给出最小位置的作图方法;文[2]用坐标法探求直角三角形的最大内接直角三角形,但错误较多,实不敢苟同.譬如“记E(t,0)(0≤t<b)”,条件应为0≤t≤b;“令直线DE的方程为y=k(x-t)(k>-ab)”,条件應为k>0或k≤-ab(由于直线AB的斜率为-ab);去绝对值混乱;定理2△DEF面积的最大值严重错误.
为此,本文分别用二次函数法和几何法探究△DEF面积的最值,其中探究△DEF面积的最小值及最小位置的作图方法有别于文[1].2 最值的探究
解法1 二次函数法
如图1,分别过点C,E,F作AB的垂线段,垂足分别为H,M,N.
设AM=y,BN=x.易得BH=a2c,AH=b2c,CH=abc.
由tanA=ab=EMy得EM=ayb;由tanB=ba=NFx得NF=bxa.
易得△DNF∽△EMD,所以DEDF=MDNF=EMDN=λ.所以MD=λbxa,DN=ayλb.
所以x+λbxa+y+ayλb=c,解得y=λbca+λb-λbxa.
S△DEF=12DE·DF=λ2·DF2=λ2(b2x2a2+a2y2λ2b2)=λ2[b2x2a2+a2λ2b2(λbca+λb-λbxa)2]
=λc22a2x2-λaca+λbx+λa2c22a+λb2.
当x=λaca+λbλc2a2=a3ca+λb时,S△DEFmin=λa2c22a+λb2-λaca+λb22λc2a2=λa2b22a+λb2.
此时y=λbca+λb-λbxa=λb3ca+λb,所以tan∠NDF=NFND=bxaayλb=λb2a2·xy=ab=tanA.
所以∠NDF=∠A.所以DF∥AC.所以当DE⊥AC时,S△DEFmin=λa2b22a+λb2(如图2). 图2
下面探究S△DEF的最大值,不妨设a≥b.
(1)当点D在点H下方时,∠DFE=∠DCE<∠HCA,所以λ<ba.
此时点F在B,C之间运动,故点N在B,H之间运动,所以0≤x≤a2c.
当x=0时,S△DEF=λa2c22a+λb2;
当x=a2c时,S△DEF=λc22a2(a2c)2-λaca+λb·a2c+λa2c22a+λb2=λ1+λ2a2b22a+λb2.
下面比较λa2c22a+λb2与λ1+λ2a2b22a+λb2的大小,只需比较c2与(1+λ2)b2的大小.
c2-(1+λ2)b2=a2-λ2b2=(a+λb)(a-λb).
由于λ<ba≤ab,所以a-λb>0,即c2>(1+λ2)b2.
所以当λ<ba时,S△DEFmax=λa2c22a+λb2(如图3).
(2)当点D与点H重合时(易得λ=ba),显然S△HCB≥S△HAC,S△DEFmax=S△HCB=12·a2c·abc=a3b2c2(参考图3).
(3)当点D在点H上方时,λ>ba.此时点E在A,C之间,故点M在A,H之间,所以0≤y≤b2c.即0≤λbca+λb-λbxa≤b2c.解得aca+λb-abλc≤x≤aca+λb.
当x=aca+λb时,S△DEF=λc22a2(aca+λb)2-λaca+λb·aca+λb+λa2c22a+λb2=λb2c22a+λb2.
当x=aca+λb-abλc时,
S△DEF=λc22a2(aca+λb-abλc)2-λaca+λb(aca+λb-abλc)+λa2c22a+λb2=1+λ2a2b22λa+λb2.
下面比较λb2c22a+λb2与1+λ2a2b22λa+λb2的大小,只需比较λ2b2c2与(1+λ2)a2b2的大小.
λ2b2c2-(1+λ2)a2b2=λ2b4-a2b2=b2(λb+a)(λb-a).
①当λ=ab时,λ2b2c2=(1+λ2)a2b2.S△DEFmax=λb2c22a+λb2=bc28a.
此时λ=tanA,所以∠DFE=∠DCE=∠A.所以DC=DA,即点D为AB的中点O(如图4).图4
②当λ>ab时,λ2b2c2>(1+λ2)a2b2.S△DEFmax=λb2c22a+λb2(如图5,点D在O,B之间).
③当ba<λ<ab时,λ2b2c2<(1+λ2)a2b2.S△DEFmax=1+λ2a2b22λa+λb2(如图6,点D在H,O之间).图5图6
综上,在a≥b条件下,当点D在A,H之间(不含A,H;此时λ<ba)时,S△DEFmax=λa2c22a+λb2(如图3);当点D与点H重合(λ=ba)时,S△DEFmax=S△HCB=a3b2c2(参考图3);当点D在H,O之间(不含O;此时ba<λ<ab)时,S△DEFmax=(1+λ2)a2b22λa+λb2(如图6);当点D与点O重合(λ=ab)时,S△DEFmax=bc28a(如图4);当点D在O,B之间(不含B;此时λ>ab)时,S△DEFmax=λb2c22a+λb2(如图5).
解法2 几何法
S△DEF=12·DE·DF=12λ·DE2.因此S△DEF的最值取决于DE的最值.
由垂线段最短知,当DE⊥AC时,S△DEF最小,如图2.
tanA=ab=DEAE=DEb-DF=DEb-DEλ,解得DE=λaba+λb,
所以S△DEFmin=12λ(λaba+λb)2=λa2b22a+λb2.
下面分情况探究S△DEF的最大值,不妨设a≥b.记斜边上的高为CH,斜边中线为CO.
(1)当点D在点H或点H下方时,图7是△DEF的两个极端位置.
由B,C,E,D四點共圆得∠DEE′=∠ABC;而∠DE′E>∠A≥∠ABC,故∠DE′E>∠DEE′,所以DE>DE′.故S△DEF>S△DE′F′.
tanA=ab=DEAD=DEc-DF=DEc-DEλ,解得DE=λaca+λb.
所以S△DEFmax=12λ(λaca+λb)2=λa2c22a+λb2,此时位置如图7中的△DEF(当点D在点H时位置为△HCB).图7
(2)当点D在点O处时,图8是△DEF的两个极端位置,显然DE=DE′,故S△DEFmax=S△DE′F′=12λ(c2)2=c28λ.而λ=tan∠OAC=ab,所以S△DEFmax=bc28a.图8
(3)当点D在H,O之间时,图9是△DEF的两个极端位置.
由OC=OA得∠OAC=∠OCA>∠DCA,所以DE>DE′.故S△DEF>S△DE′F′.
过D作DG⊥BC于G.
因为λ=tan∠DFE=tan∠CDG=CGDG,tanB=ba=DGBG=DGa-CG,所以DG=aba+λb.
因为tan∠DFE=λ,所以sin∠DFE=λ1+λ2=DGDF.解得DF=ab1+λ2λa+λb.
所以S△DEFmax=λ2·DF2=1+λ2a2b22λa+λb2,此时位置如图9中的△DEF.图9
(4)当点D在O,B之间时,图10是△DEF的两个极端位置.
由OC=OA得∠OAC=∠OCA<∠DCA,所以DE<DE′.故S△DEF<S△DE′F′.
过D作DG⊥BC于G.由③得DG=aba+λb.
因为cos∠GDF′=cosB=ac,所以DGDF′=ac,解得DF′=bca+λb.
所以S△DEFmax=λ2·DF′2=λb2c22a+λb2,此时位置为图10中的△DE′F′.图10
3 最小位置的作图方法
当DE⊥AC时,S△DEF最小.由此可给出S△DEF最小时的准确位置及作图方法.
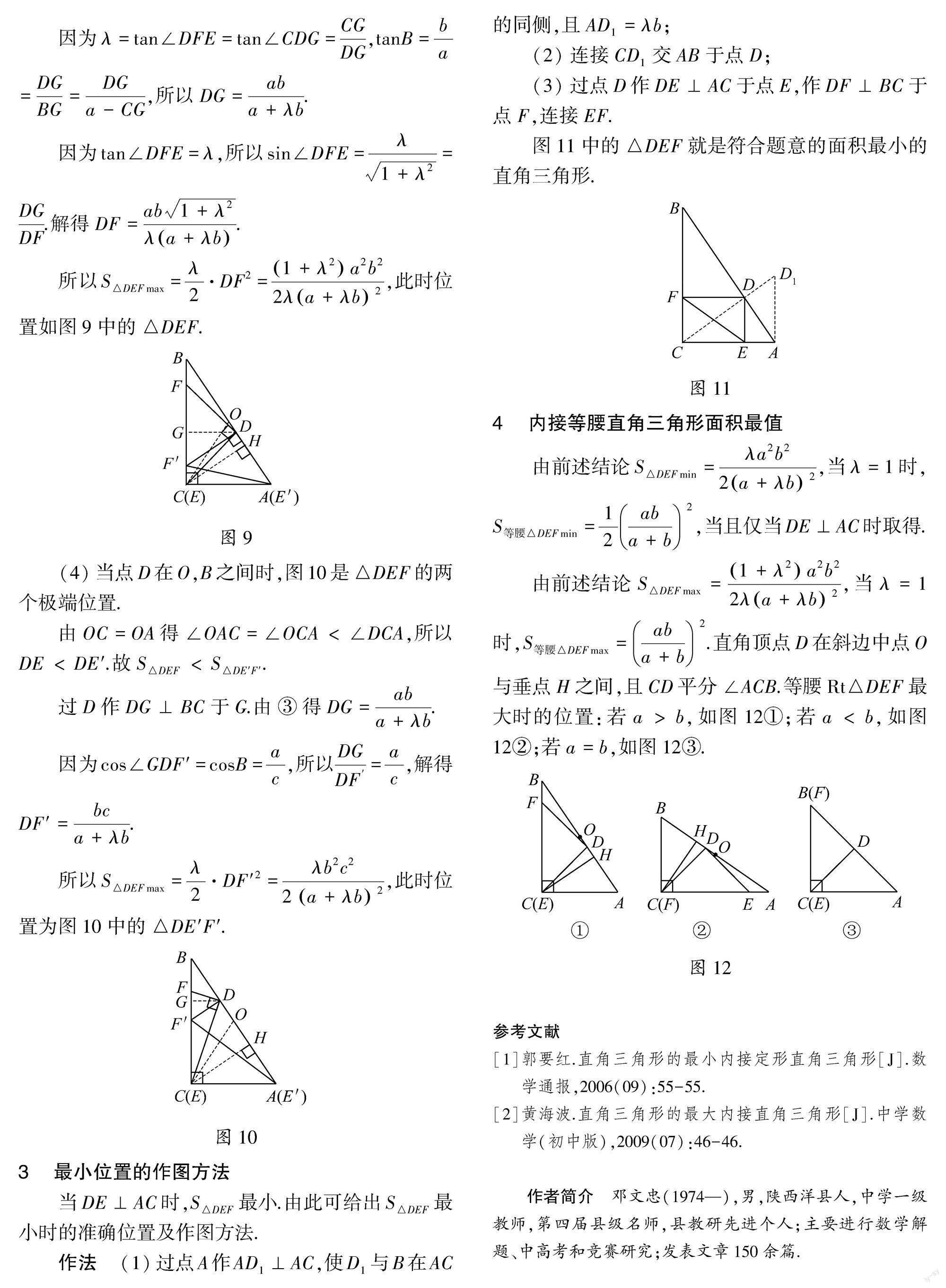
作法 (1)过点A作AD1⊥AC,使D1与B在AC的同侧,且AD1=λb;
(2)连接CD1交AB于点D;
(3)过点D作DE⊥AC于点E,作DF⊥BC于点F,连接EF.
图11中的△DEF就是符合题意的面积最小的直角三角形.图11
4 内接等腰直角三角形面积最值
由前述结论S△DEFmin=λa2b22a+λb2,当λ=1时,S等腰△DEFmin=12aba+b2,当且仅当DE⊥AC时取得.
由前述结论S△DEFmax=1+λ2a2b22λa+λb2,当λ=1时,S等腰△DEFmax=aba+b2.直角顶点D在斜边中点O与垂点H之间,且CD平分∠ACB.等腰Rt△DEF最大时的位置:若a>b,如图12①;若a<b,如图12②;若a=b,如图12③.
参考文献
[1]郭要红.直角三角形的最小内接定形直角三角形[J].数学通报,2006(09):55-55.
[2]黄海波.直角三角形的最大内接直角三角形[J].中学数学(初中版),2009(07):46-46.作者简介 邓文忠(1974—),男,陕西洋县人,中学一级教师,第四届县级名师,县教研先进个人;主要进行数学解题、中高考和竞赛研究;发表文章150余篇.
