基于发展推理能力的数学实验教学设计与反思

林锋

［摘 要］数学实验教学是“做数学”的教学，是培养学生推理能力的重要平台。文章以“探究圆心运动路径的问题”数学实验课为例，探讨发展学生推理能力的数学实验教学设计，以期给当前数学实验教学一些启示。

［关键词］数学实验；推理能力；初中数学

［中图分类号］ G633.6 ［文献标识码］  A ［文章编号］ 1674-6058（2023）26-0020-03

推理能力是学生必备的关键能力。数学实验教学是“做数学”的教学，是培养学生推理能力的重要平台。在近期举行的数学实验专题活动中，笔者以培养学生的推理能力为目标，主讲了“探究圆心运动路径的问题”数学实验课，并对数学实验课的教学设计做了全面剖析。现进行相关介绍，与同仁们分享。

一、教学内容分析

本次数学实验课的授课时间为45分钟，授课对象是九年级学生，他们已学完“圆”的内容，笔者将全班学生分为8个小组，为学生准备以下实验工具：半径为2 cm的圆形塑料片一个，半径为5 cm的圆形塑料圈一个，边长为6 cm的正方形框架一个，边长为5 cm的正五边形框架一个，万花尺一套等。

根据教学内容与培养目标，笔者给本节数学实验课确定如下教学目标：（1）通过数学实验，探究圆在圆、正方形、正五边形内部滚动时圆心经过的路径长，探究圆在圆、正方形、正五边形外部滚动时圆心经过的路径长；（2）通过动手滚动、观察路径、猜想结论、归纳总结发展学生的合情推理能力，通过代数计算与几何证明等实验活动发展学生的演绎推理能力；（3）在数学实验活動中，不断积累数学活动经验，感受数学文化的魅力。

二、教学过程设计与分析

［数学实验1］圆在图内部滚动时，圆心经过的路径探究。

1.小圆与大圆内切时滚动，小圆圆心运动的路径长探究

操作流程：如图1所示，把半径为2 cm的圆形塑料片放入半径为5 cm的圆形塑料圈内，两圆内切，用笔尖插入小圆片的圆心，让小圆在大圆内部滚动一周，在滚动过程中始终保持内切，观察笔尖的运动路径是什么图形。

计算猜想与验证：你能计算小圆圆心O的运动路径长吗？如果大圆的半径为R，小圆的半径为r，那么小圆圆心运动的路径长是多少？如果小圆按住不动，让大圆运动，并始终保证两圆内切，那么大圆圆心的运动路径长是多少？为什么？

生1：我们小组经过操作，观察到笔尖的运动路径是一个圆。

生2：笔尖的运动路径是一个圆，这个圆的圆心是大圆圆心[O']，半径是5-2=3（cm），所以小圆圆心O的运动路径长为6π。

生3：如果大圆的半径为R，小圆的半径为r，那么小圆圆心运动的路径仍是一个圆，圆心是大圆圆心[O']，半径是（R-r），所以小圆圆心运动的路径长为2（R-r）π。

生4：如果小圆按住不动，让大圆运动，并始终保证两圆内切，那么大圆圆心的运动路径还是一个圆，这个圆的圆心是小圆圆心O，半径是（R-r），所以大圆心的运动路径长为2（R-r）π。

设计意图：学生已经学完了“圆”的全部知识，两圆始终内切学生知道该如何去做，小圆在大圆内部运动，学生操作比较容易。低起点的教学能使学生快速融入课堂，从操作到猜想再到计算推理，既培养了学生的合情推理能力，也培养了学生的演绎推理能力。

2.圆与正多边形的边内切时滚动，圆心运动路径长探究

操作流程：如图2所示，将半径为2 cm的圆形塑料片放在边长为6 cm的正方形框架内，小圆片与正方形的边始终保持相切，将笔尖插入小圆片的圆心，让小圆片在正方形内滚动一周，观察小圆片圆心的运动路径是什么图形。如图3所示，将半径为2 cm的圆形塑料片放在边长为5 cm的正五边形框架内，小圆片与正五边形的边始终保持相切，将笔尖插入小圆片的圆心，让小圆片在正五边形内滚动一周，观察小圆片圆心的运动路径是什么图形。

计算猜想与验证：如图2，你能计算小圆片圆心的运动路径长吗？如图3，你能计算小圆片圆心的运动路径长吗？如图4所示，如果将半径为r的圆形塑料片放在边长为m（[m>2r]）的正多边形框架内，小圆片与正多边形的边始终保持相切，将笔尖插入小圆片的圆心，让小圆片在正多边形内滚动一周，小圆片圆心的运动路径是什么图形？如何计算小圆片的运动路径长？

生5：在图2中，小圆片在正方形内滚动，并保证圆与正方形的边相切，我们小组观察到圆心的运动路径是一个正方形，这个正方形的边长是2 cm，所以小圆心的运动路径长为8 cm。

生6：在图3中，小圆片在正五边形内滚动，并保证圆与正五边形的边相切，我们小组观察到圆心的运动路径是一个正五边形，这个正五边形的边长经测量约为2 cm，所以小圆心的运动路径长为10 cm。

生7：在图4中，小圆片在正多边形内滚动，并保证圆与正多边形相切，我们猜想小圆片圆心的路径是一个正多边形，且边数与原正多边形边数相同，但不知如何计算圆片的运动路径长。

设计意图：从正方形、正五边形到正[n]边形体现了由特殊到一般的数学思想，学生借助抽象与类比提出猜想，最后运用演绎推理证明验证了猜想的合理性。

［数学实验2］圆在多边形外部滚动时运动路径长探究。

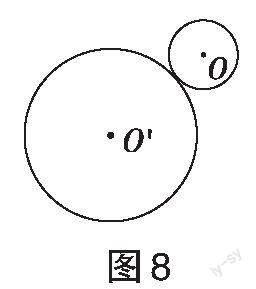
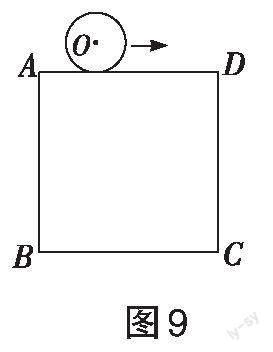
操作与观察：（1）如图8所示，将半径为2 cm的小圆片放在半径为5 cm的圆圈外部滚动，并始终保持小圆与大圆相切，将笔尖插入小圆圆心，观察小圆圆心的运动路径是什么图形。（2）如图9所示，将半径为2 cm的小圆片放在边长为6cm的正方形外部滚动，并始终保持小圆与正方形的边相切，将笔尖插入小圆圆心，观察小圆圆心的运动路径是什么图形。（3）如图10所示，将半径为2 cm的小圆片放在边长为5 cm的正五边形外运动，并始终保持小圆与正五边形的边相切，将笔尖插入小圆圆心，观察小圆圆心的运动路径是什么图形。

计算猜想与验证：你能计算图8中小圆圆心运动路径长是多少吗？图9中，小圆圆心的运动路径长是多少？图10中，小圆圆心的路径长是多少？如图11所示，将半径为r的圆片放在多边形的外部滚动，这个多边形的周长为L，并始终保持圆与多边形的边相切，那么小圆圆心的运动路径是什么图形？小圆圆心的运动路径长是多少？为什么？

生8：通过操作，我们小组发现，在图8中，小圆圆心的运动路径是一个圆，这个圆的圆心是大圆圆心，半径是两个圆的半径之和，即[2+5=7]（cm），如图12所示，所以小圆圆心的运动路径长为14π。

生9：通过操作，我们小组发现，在图9中，小圆圆心的运动路径是一个圆角正方形，如图13所示，它由四条线段与四段圆弧组成，这四条线段的长等于正方形的周长，即[6×4=24]（cm），四段圆弧都相等，每段圆弧的圆心角度数是90°，半径是2 cm，所

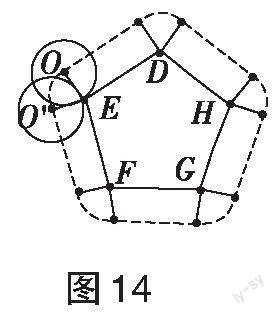
生10：通过操作，我们小组发现，在图10中，小圆圆心的运动路径是一个圆角正五边形，如图14所示，但不知如何计算小圆圆心的运动路径长。

师生活动：如图14所示，小圆在正五边形的外部滚动，当小圆滚过每个顶点时，都形成一段圆弧，这五段圆弧的长度都相等，那么每段圆弧的半径与圆心角分别是多少？当小圆滚过顶点E时，小圆半径OE從垂直于DE的状态，到O′E垂直于EF的状态，所以圆弧的半径就是小圆的半径2 cm，此时[∠OED=90°]，[∠O′EF=90°]，[∠DEF=108°]，所以[∠OEO′=72°]，因为这五段圆弧的半径都相等，均为2 cm，将它们合在一起，恰好构成一个半径为[2 cm]的圆，这个圆的周长为4π，所以这五段圆弧长之和为4π，运动路径中的五条线段等于五边形的周长[=5×5=25 cm]，所以在图10中，小圆圆心的运动路径长为（[25+4π]） cm。

如图11所示，当半径为r的小圆片在周长为L的多边形的外部滚动时，小圆圆心的运动路径是什么图形呢？运动路径长是多少？我们可以从小圆片在正方形外部滚动，小圆片在正五边形外部滚动时，运动路径及其长度中找到活动经验，首先小圆圆心的运动路径也是由线段与圆弧组成的圆角多边形，其中的线段长之和等于多边形的周长L，其中的圆弧长之和等于小圆的周长，所以半径为r的圆在周长为L的多边形外部滚动时，小圆圆心的运动路径长=L+2πr。

设计意图：实验设计由内而外，思维的难度与推理的难度也在增大。当小圆片在正方形外部滚动时，有部分学生认为其运动路径是正方形，产生错误的原因是学生根据小圆在大圆的外部滚动时运动路径是一个圆这一经验，认为小圆在正方形的外部滚动时运动路径也应是一个正方形，这是知识的负迁移造成的结果。笔者让学生实际操作，通过动手操作，学生发现小圆圆心的运动路径并不是一个圆，而是一个圆角正方形。有了这次的经验教训，学生在操作正五边形时谨慎多了，通过实际操作，学生发现小圆在正五边形外部滚动时，圆心拐过顶点时，形成了一小段圆弧，而不是一个点。在猜想验证部分，由数字变为字母，从特殊到一般，笔者始终让学生思考两个关键点：一是小圆圆心的运动路径由几部分组成？二是顶点处旋转的角度之和是360°吗？学生结合已有的活动经验提出自己的猜想，然后用演绎推理的方法进一步论证，最后得到了“半径为r的圆在周长为L的多边形外部滚动时，小圆圆心的运动路径长=L+2πr”的结论。

［数学实验3］万花尺的美妙图案。

如图15所示，这是一副万花尺，通过笔尖可以使小圆在大圆内滚动起来，在小圆内有数个小孔，这些小孔并不是均匀分布的，将笔尖插入不同的小孔，经过若干次在圆内滚动后，画出的图案都不一样。

如图16和图17所示是学生利用万花尺与彩笔画出的美丽图案。

设计意图：让学生自己动手画出与本次数学实验课相关的“繁花曲线”，充分体验数学实验之美。

三、教后反思

（一）有效的问题情境是发展学生推理能力的重要载体

问题情境可引导学生自主探索数学结论，有利于发展学生的推理能力。第一，笔者设计问题情境，让学生用笔尖插入小圆片的圆心，在滚动过程中始终保持内切，观察笔尖的运动路径是什么图形，计算小圆圆心O的运动路径长，激发了学生探究的兴趣与欲望。第二，笔者设计开放性问题情境，在开放性问题情境的驱动下，学生在 “做数学”中主动探究，促进了学生推理能力的发展。

（二）丰富的活动空间是发展学生推理能力的有力保障

新课标指出，通过多样化的活动来培养学生的推理能力。本节课的数学实验以“做”为支架，引导学生边做边学。在做数学实验的过程中，学生经历了猜想、操作、观察、质疑、再操作等推理过程。不难发现，数学实验活动为学生推理能力的发展提供了较大的空间，使学生积累了丰富的活动经验，提升了数学学科核心素养。