追本溯源：2022年全国新高考Ⅱ卷第12题的解法研究

黄国强 秦 君

⦿四川外语学院重庆第二外国语学校

1 试题再现

若x，y为实数，满足x2+y2-xy=1，则( ).

A.x+y≤1 B.x+y≥-2

C.x2+y2≥1 D.x2+y2≤2

2 试题分析

全国新高考Ⅱ卷第12题，利用已知代数关系考查不等关系.该试题可参考人教A版数学必修一(2019版)第二章复习参考题综合应用第5题，因此我们很容易想到利用不等式相关知识寻找突破口，同时还可以利用方程思想、换元思想等通法和赋值法(秒杀)进行判断.

3 思维导图

本题目具体解题思路见图1.

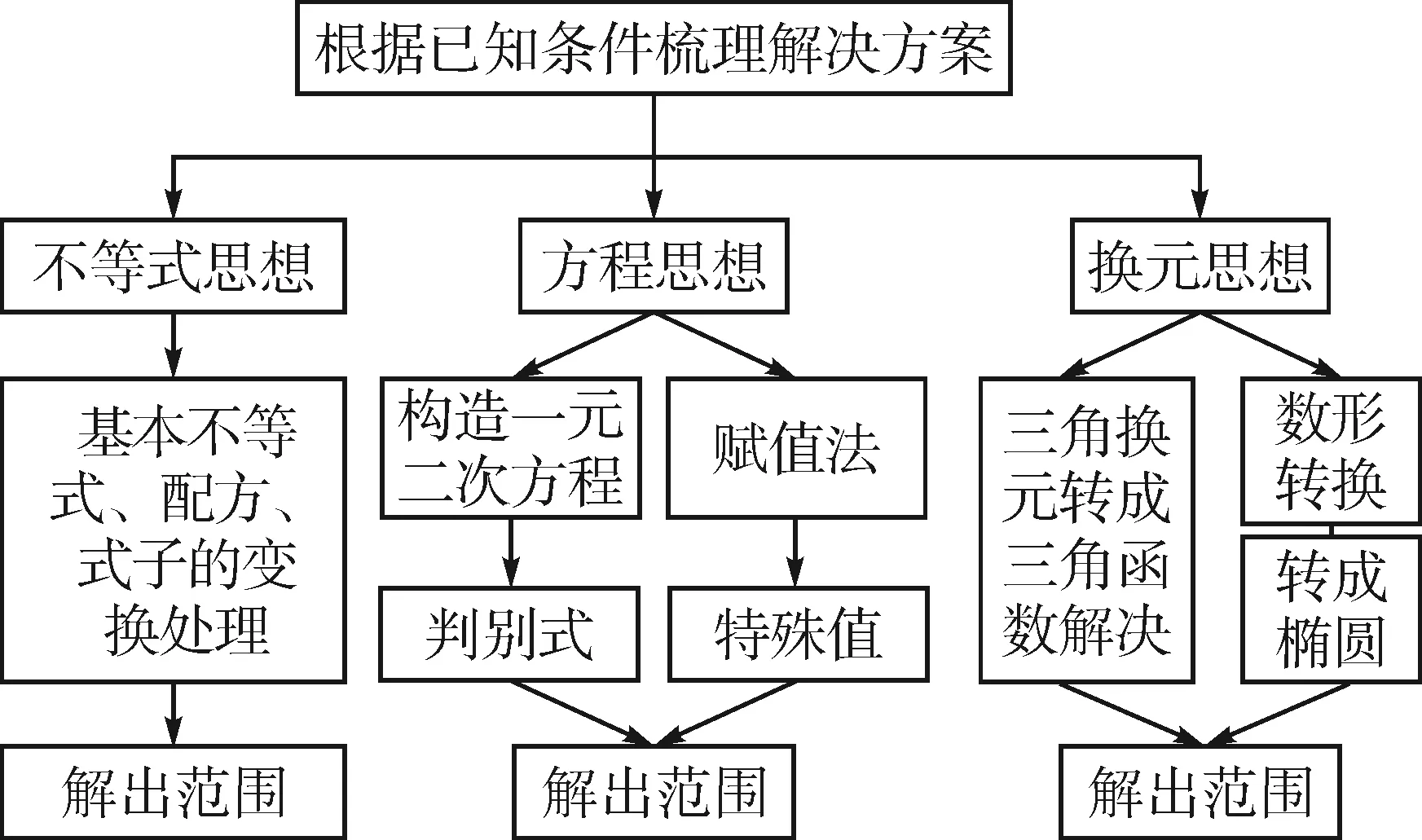
图1

4 具体解法

方法1:不等式法.

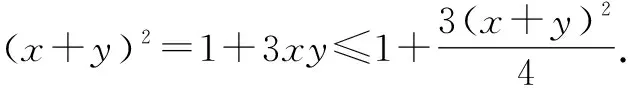
由(x+y)2≤4，得-2≤x+y≤2.故排除选项A.

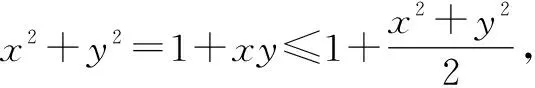
所以选择：BD.

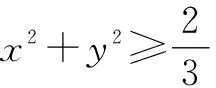
方法2：方程思想.

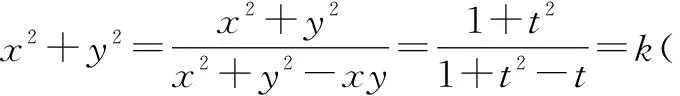
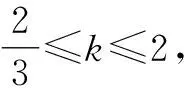
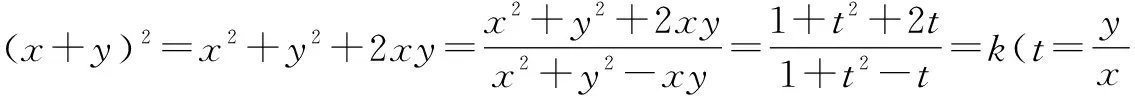
于是(k-1)t2-(k+2)t+(k-1)=0(k≠1)，则Δ=(k+2)2-4(k-1)2≥0，得k≤4，即-2≤x+y≤2，当x=0或k=1时符合条件.

方法总结：该方法采用方程思想，利用方程有解，建立判别式的不等关系.

方法3：换元法一.

解：由x2+y2-xy=1，得

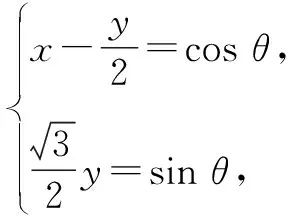
方法总结：该方法对综合能力的要求较高，学生不易想到.此解法可参考人教版教材2019选择性必修-第89页中第10题圆的参数方程.

方法4：换元法二.

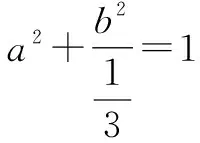
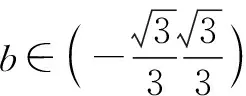
方法总结：该方法参考了文卫星编著的《挑战压轴题——高考数学》2020版第15页考点延伸第3题的解法.此方法的核心之处在于将代数关系转化为椭圆方程，巧妙换元转化成学生熟悉的知识.该解法是数转形，对数学抽象、数学建模、逻辑推理等核心素养提出了较高要求.

方法5：赋值法(秒杀).

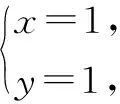
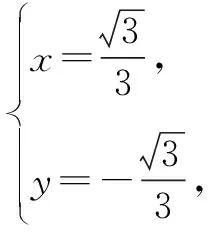
方法总结：利用等式结构特征适当赋值，巧妙地排除不符合的选项.

5 拓展延伸

对于上述解法4，实际是将代数问题巧妙地转换成几何问题，人教A版(2019版)数学选择性必修一第143页的回顾与思考中提出方程与曲线的关系“方程f(x,y)=0是曲线的方程”.

故令f(x,y)=x2+y2-xy-1=0，能否判断点(x,y)的运动轨迹(区域)呢？

答案是肯定的.下面我们介绍绘图方法，大致判断点(x,y)的轨迹区域.

不难发现f(x,y)=f(-x,-y)，f(-x,y)=f(x,-y).

接下来只讨论两种情况：

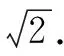
在第一象限作出图2，由f(x,y)=f(-x,-y)在第三象限作出图3.

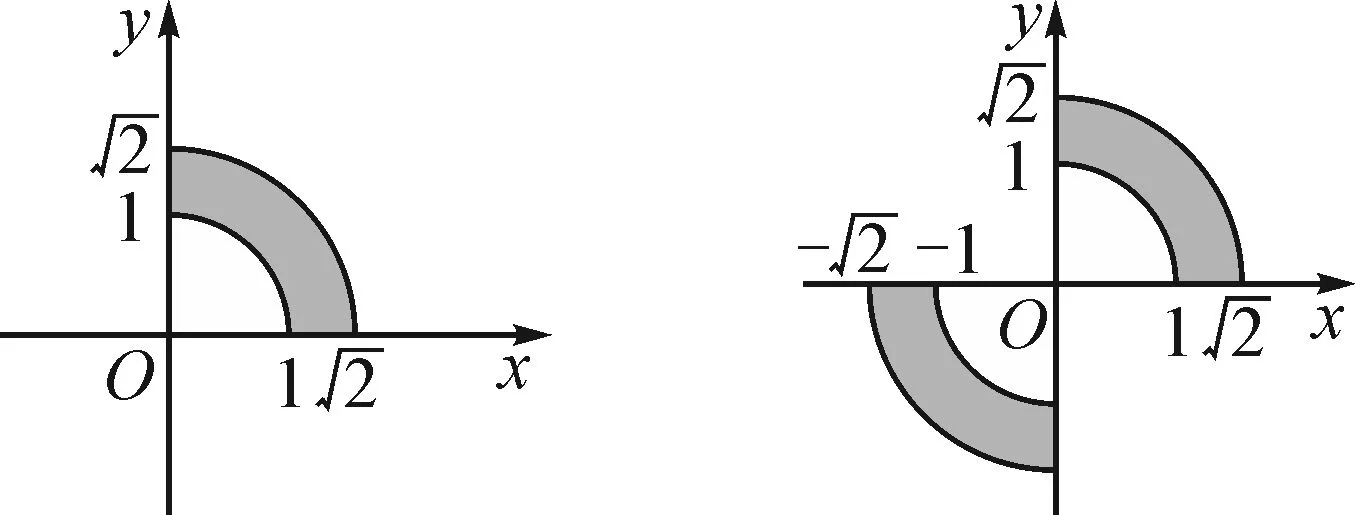
图2 图3

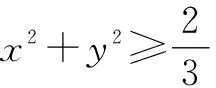
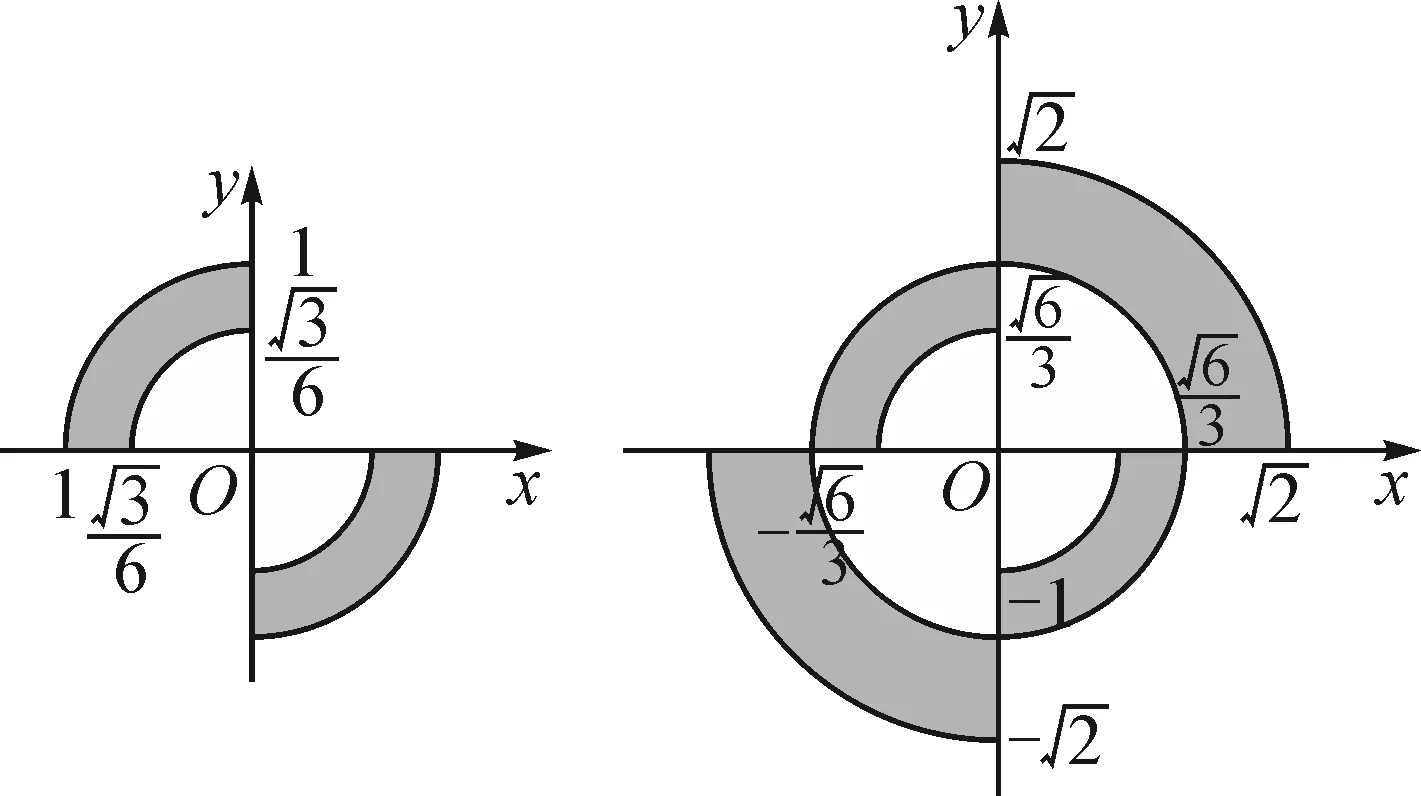
图4 图5

选项分析：图5为点(x,y)的轨迹区域，是人教版必修五(2008版)第三章简单的线性规划知识，选项A，B表示点(x,y)与直线x+y=1，x+y=-2的位置关系，选项C，D表示点(x,y)与圆x2+y2=1，x2+y2=2的位置关系.

6 试题链接

给两个试题供读者练习.

链接1若正实数x，y满足2x+y+6=xy，则xy的最小值是.

链接2已知正实数x，y，z满足x2+y2+z2=1，则xy+yz的最大值为.