L-代数上的赋值

2022-08-02高小燕

榆林学院学报 2022年4期

高小燕

(榆林学院数学与统计学院，陕西榆林 719000)

Rump在2008年提出L-代数[1],它具有多值逻辑，直觉逻辑和量子逻辑的特点，因此L-代数是值得研究的非经典逻辑代数。随后，Yang等人讨论了格效应代数和L-代数的关系[2]，该团队还证明了正交模格也是L-代数[3]。Ciungu 证明了交换的KL-代数是BCI-代数[4]。在[5]中，Rump从代数、几何和拓扑的角度给出了L-代数的一些例子。

Busneag首先在希尔伯特代数上定义了赋值，并借助赋值给出了一种度量,证明了蕴含运算在该度量下是一致连续的[6]。在此基础上，Lee在BE-代数引入了伪赋值，利用伪赋值给出了伪度量，并证明了其上的二元运算是一致连续的[7]。近些年，Mehrshad等人在BCK-代数上定义了伪赋值，证明了在由伪赋值诱导的拓扑下,L-代数上的运算是连续的[8]。

本文在L-代数中引入强伪赋值和伪赋值的概念，讨论他们之间的关系。接着给出强伪赋值和伪赋值的构造，最后给出了强伪赋值与态可以相互诱导的公式。

1 预备知识

定义1[1]设L非空集合，称(L，→，1)为L-代数，若它满足以下条件：对于∀x,y,z∈L,

(L1)x→x=1,x→1=1,1→x=x；

(L2)(x→y)→(x→z)=(y→x)→(y→z) ；

(L3) 若x→y=y→x=1，则x=y 。

在L上定义关系为 x≤y⟺x→y=1，对于∀x,y∈L；可以证明它是偏序关系。若L有最小元0，则称L是有界L-代数。

例1设L={0,a,b,c,1}，→运算定义如下：

→0abc1011111ab1b11baa111c0ab1110abc1

则(L,→,1)是一个有界L-代数。

定义2 设(L,→,1)是一个L-代数，R是一个实数集，φ∶L→R，给出以下条件，对于∀x,y∈L：

(pv1)φ(1)=0 ；

(pv2) 若φ(x)=0,则x=1

(pv3) φ(y)≤φ(x→y)+φ(x)；

(pv4)φ(y)+φ(y→x)=φ(x→y)+φ(x)。

若φ满足(pv1)和(pv3),则称φ是伪赋值；若φ满足(pv1)和(pv4),则称φ是强伪赋值；若φ满足(pv1),(pv2)和(pv3),则称φ是赋值；若φ满足(pv1)-(pv4)则称φ是强赋值。

例2 设(L,→,1)是L-代数(见例1)，在L上定义实值函数φ如下

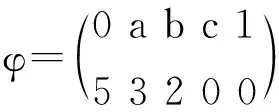
可以验证φ满足(pv1),(pv3) (pv4),从而φ是伪赋值和强伪赋值。但这个L-代数无强赋值。这是因为，假设φ是强赋值，则它满足(pv4)，令y=c,x=0,则由φ(y)+φ(y→x)=φ(x→y)+φ(x)得φ(c)+φ(0)=φ(1)+φ(0)，由于φ(1)=0，因此φ(c)=0，这与(pv2)矛盾。

定义3 设L是一个L-代数，L上Bosbach态是一个函数s∶L→[0,1],满足以下条件：

(s1) s(1)=1 ；

(s2) s(x)+s(x→y)=s(y)+s(y→x)。

例3 设(L,→,1)是L-代数(见例1)，在L上定义实值函数s如下

可以验证s是(L,→,1)上的Bosbach态。

2 主要结论

命题1 设φ是L上的一个伪赋值，则以下命题成立：

(1)φ是反序的，即x≤y⟹φ(x)≥φ(y)；

(2)φ(x)≥0。

证明(1)x≤y设，则x→y=1，可得φ(y)≤φ(x→y)+φ(x)=φ(1)+φ(x)=φ(x)即φ(y)≤φ(x)。

(2) 因为x≤1，φ(1)=0且φ是反序的，所以φ(x)≥φ(1)=0。

推论1 强伪赋值是是伪赋值。

证明设φ是L上的一个强伪赋值，则它满足φ(y)+φ(y→x)=φ(x→y)+φ(x)，由命题1的(2)知φ(y→x)≥0，因此φ(y)≤φ(x→y)+φ(x)。

下面给出例子，说明伪赋值不是强伪赋值。

例4 设L={0,a,b,c,d,1}，→运算定义如下：

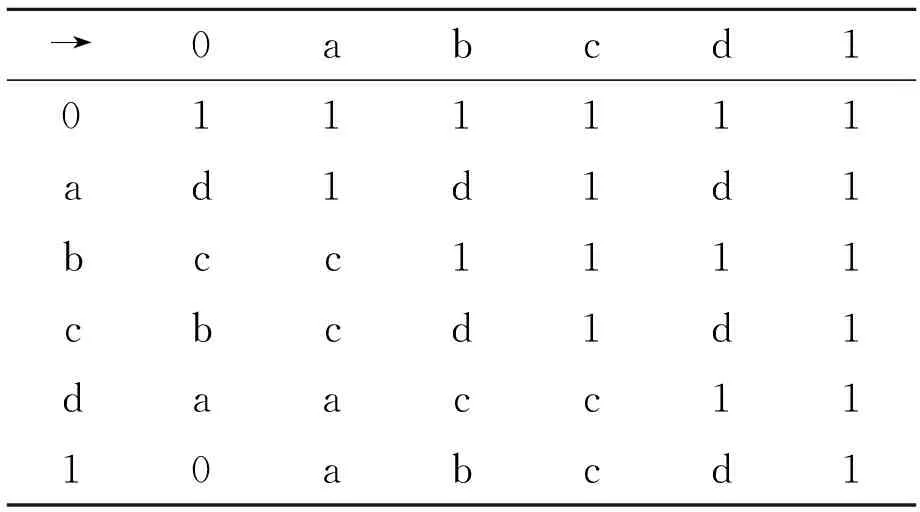
→0abcd10111111ad1d1d1bcc1111cbcd1d1daacc1110abcd1

则(L,→,1)是一个L-代数。在L上定义实值函数φ如下

可以验证而φ是L上的伪赋值，但它并不是L上的强伪赋值，因为2=φ(0→a)+φ(0)≠φ(a→0)+φ(a)=3。

定理1 (1) φ是L上的伪赋值，则φ1和φ2也是伪赋值；

(2) φ是L上的赋值，则φ1和φ2也是赋值；

(3) φ是L上的强伪赋值，则φ1也是强伪赋值；

(4) φ是L上的强赋值，则φ1也是强赋值。

证明(1) 因为φ是L-代数上的伪赋值，所以φ满足以下条件：

(pv1)φ(1)=0 和(pv3) φ(y)≤φ(x→y)+φ(x)。

由于φ1(x)=wφ(x),(w>0)我们有φ(1)=wφ(1)=0，即(pv1)成立；φ1(x→y)+φ1(x)=wφ(x→y)+wφ(x)≥wφ(y)=φ1(y)，从而可得(pv3)成立，这就证明了φ1为L-代数上的伪赋值。

下面验证φ2满足(pv3)，从而φ2是伪赋值。当x=y=1时，结论显然成立。

当x≤y且x≠1时，此时分两种情况，情况1，y=1，结论显然成立；情况2，y≠1，我们有φ2(x→y)+φ2(x)=φ2(1)+φ2(x)=φ2(x)=wφ(x)+b≥wφ(y)+b=φ2(y)。

这是因为φ是伪赋值，由命题1知φ是反序的。

当x≤y不成立时, 此时分两种情况, 情况1，x=1，

φ2(x→y)+φ2(x)=φ2(1→y)+φ2(1)=φ2(y)。

情况2，x严格小于1，此时y严格小于1，因此φ2(x→y)+φ2(x)=wφ(x→y)+b+wφ(x)+b≥wφ(y)+b=φ2(y)。

(2) 设φ是L-代数上的赋值，则φ(x)=0,一定有x=1。若φ(x)=0则0=φ1(x)=wφ(x),又因为w>0,从而φ(x)=0，因此有x=1。由(1)知φ1是L-代数上的赋值。

若φ2(x)=0则必有x=1。否则φ2(x)=wφ(x)+b≥b>0矛盾。由(1)知φ2是L-代数上的赋值。

(3) 由(1)知，φ1满足(pv1),下面证明φ1满足(pv4)，从而φ1也是强伪赋值。

φ1(y)+φ1(y→x)=wφ(y)+wφ(y→x)=wφ(x→y)+wφ(x)=φ1(x→y)+φ1(x)。

(4) 由(2)和(3)知(4)是成立的。

下面的例子说明：φ是L上的强伪赋值，但φ2不是L上的强伪赋值。

例5 设L={0,a,b,c,d,1}，→运算定义见例4，在L上定义实值函数φ如下

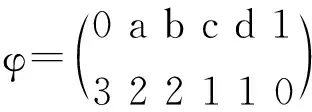
但φ2并不是L上的强伪赋值，这是因为

4=φ2(0→b)+φ2(0)≠φ2(b→0)+φ2(b)=5。

定理2 设L是一个L-代数，s是L上的Bosbach态。定义一个实值函数φt(x)=t-ts(x)，∀x∈L,t∈R且t≥0，则φt是L上的一个强伪赋值。

证明首先证明φt满足(pv1)， φt(1)=t-ts(1)=t-t=0。

其次证明φt满足(pv4)，

φt(x→y)+φt(x)=t-ts(x→y)+t-ts(x)=2t-t(s(x→y)+s(x))，由(s2)得s(x)+s(x→y)=s(y)+s(y→x)，从而2t-t(s(x→y)+s(x))=2t-t(s(y)+s(y→x)=(t-ts(y))+(t-ts(y→x))=φt(y→x)+φt(y)，因此φt是L上的强伪赋值。

定理3 设L是一个L-代数，φ是L上的强伪赋值。令s(x)=1-φ(x)，则s是L上的一个Bosbach态。

证明显然s(1)=1-φ(1)=1-0=1,从而满足(s1)。下面证明 (s2)成立。由s(x)定义知

s(x)+s(x→y)=1-φ(x)+1-φ(x→y)，因为φ满足(pv4)，即φ(y)+φ(y→x)=φ(x→y)+φ(x)，从而有s(x)+s(x→y)=1-φ(x)+1-φ(x→y)=1-φ(y)+1-φ(y→x)=s(y)+s(y→x)，因此s是L上的一个Bosbach态。