求曲线轨迹方程的五种常用方法例析

李春林

⦿甘肃省天水市第九中学

求曲线轨迹方程的问题，历来是高考数学的重点、难点问题之一.许多学生面对这类问题，常常感到束手无策.为此，笔者综合平时的教学，梳理归纳出以下五种求轨迹方程的常用方法.

1 直接法

若动点M满足的几何条件是用等量关系给出的，求动点M的轨迹方程可按建系、设点、代入、化简、证明五个步骤进行.

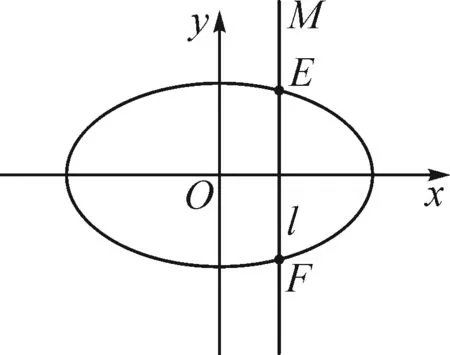
图1

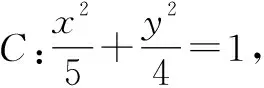
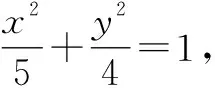
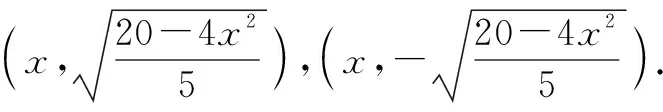
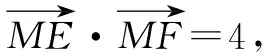
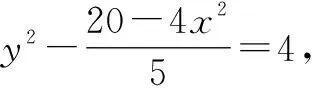
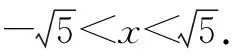
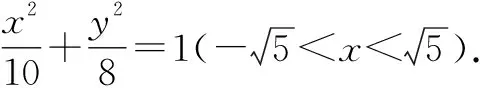
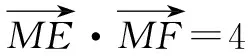
2 定义法

若动点M的轨迹符合常见曲线(直线、圆、圆锥曲线等)的定义时，则可抓住曲线的几何特征，直接得出点M的轨迹方程.

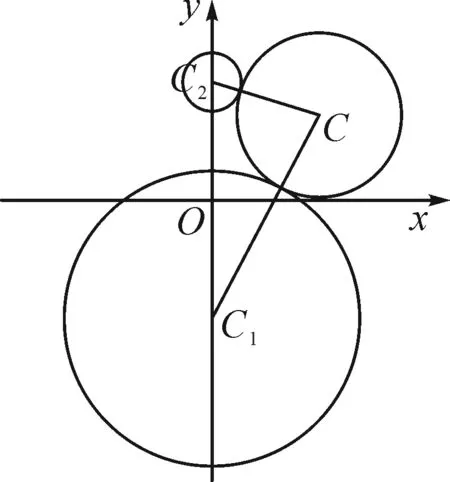
图2

典例2如图2，已知圆x2+(y+4)2=25的圆心为C1，圆x2+(y-4)2=1的圆心为C2,某动圆C分别与圆C1、圆C2相外切，求动圆圆心C的轨迹方程.

解：由已知，点C1(0,-4),C2(0,4),r1=5,r2=1.

设动圆C的半径为r,则由圆C分别与圆C1、圆C2相外切，得|CC1|=r+5，|CC2|=r+1.

所以|CC1|-|CC2|=4<8.

即点C到两定点C1,C2的距离之差为常数4，所以动圆圆心的C的轨迹是以C1,C2为焦点的双曲线的上支.

由题意，得2a=4,2c=|C1C2|=8.

所以b2=c2-a2=12.

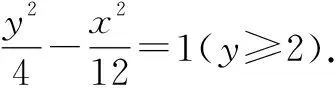
点评：利用已知条件，分析得出动圆圆心C的轨迹符合双曲线(上支)定义，从而结合已知条件，直接得出轨迹方程.

3 相关点法

如果两点P，Q之间存在某种确定的运动规律，并且这两点中某点的轨迹方程是已知的，这时可以建立点P，Q的坐标关系，通过代换求出另一点的轨迹方程.

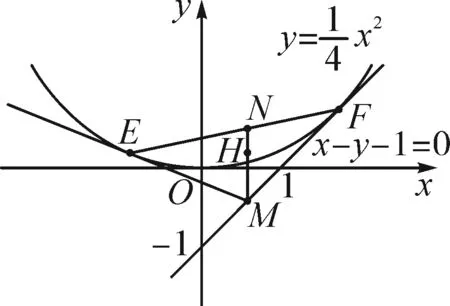
图3

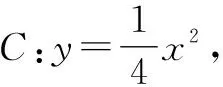
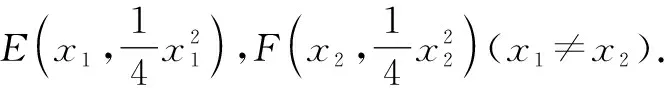
①

切线MF的方程为

②

由①②联立,得M点横、纵坐标分别为

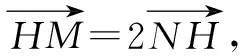
③

④

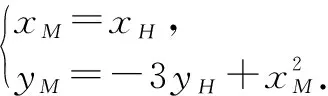
由点M在直线l上，得xM-yM-1=0.

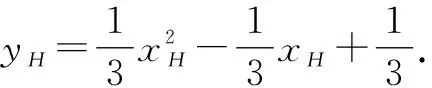
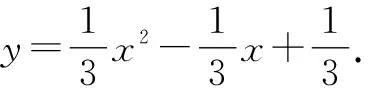
点评：确定点H与点M的坐标关系后，由点M在已知直线上，通过代换即可求出点H轨迹方程.这类问题确立两动点坐标关系是解题的关键.

4 参数法

图4

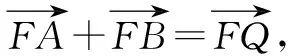
解:由题意，可设直线l的方程为y=kx-1,设点Q(x,y),A(x1,y1),B(x2,y2).

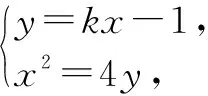
因为直线l与抛物线C：x2=4y交于A，B两点,所以x1+x2=4k,且Δ=16k2-16>0.

解得k<-1，或k>1.

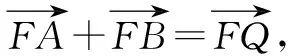
(x1，y1-1)+(x2,y2-1)=(x,y-1).

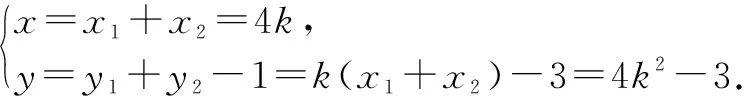
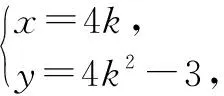
因为x=4k(k<-1，或k>1)，所以x<-4，或x>4.

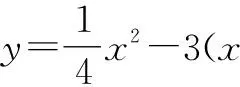
点评：引入参数k，表示直线l的斜率，进而建立动点Q的坐标与参数k之间的关系，最后消去参数k即得点Q的轨迹方程.恰当引参，建立动点Q的坐标与参数k的关系是解题的关键.

5 交轨法

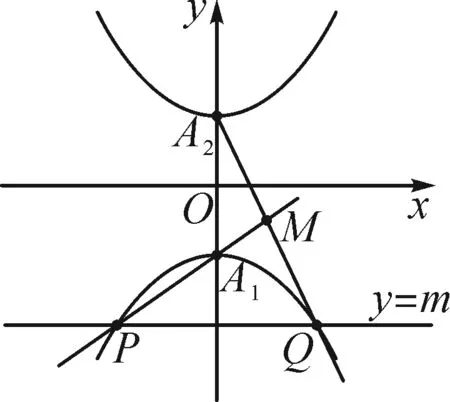
图5

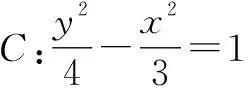
解：设P(x1，m)，Q(-x1，m)，M(x，y).

由点P在双曲线上，得

⑤

当x1≠0时，直线PA1的方程为

⑥

直线QA2的方程为

⑦

由⑥×⑦，得

⑧

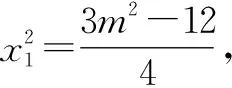
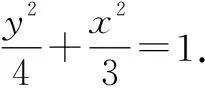
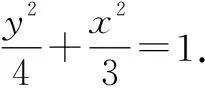
点评：巧妙地引入双参数x1与m，进而得到两动直线的方程.联立求出交点M(x，y)，然后整理出x，y，x1，m间的关系，最后再消去x1与m，即得点M的轨迹方程.

6 小结

求曲线轨迹方程的问题，涉及知识点多，范围广，交汇性强，运算与推理比较复杂.但只要理解和把握问题的本质，熟练运用上述五种常用方法，综合分析，灵活应用，就能逐渐走出求轨迹方程的困境.