复杂函数求最值 同构处理很奇妙
2023-04-15汪亚洲
汪亚洲
⦿湖北省小池滨江高级中学
洪 亮
⦿湖北省黄梅县小池镇一中
同构式是指除了变量不同外,其余地方都相同的式子[1].若方程中出现同构特征,则x1,x2可视为方程的两个根;若函数中出现同构式,可将相同结构的式子构造成一个函数,再通过求导解决问题.
1 例题展示
例已知函数f(x)=aex-lnx+lna,其中e为自然对数的底数,若对任意的正实数x,都有f(x)≥0成立,则a的最小值为.
2 一题多解
本题是在恒成立的条件下求最值,最初的想法是利用分离变量法,但是变量在多处存在,此法行不通,此时可以考虑求导,得到f(x)的最小值f(x0),然后令f(x0)≥0,从而求出a的最小值.
解法1:求导法.
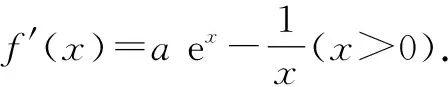
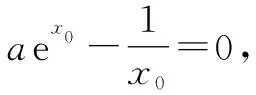
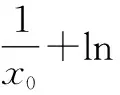
解法2:搭建同构式 (朝着tet转化).
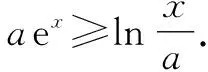
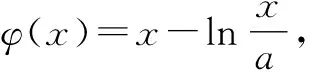
解法3:搭建同构式 (朝着tlnt转化).
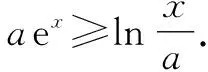
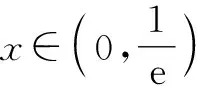
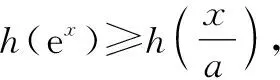
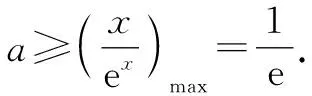
解法4:搭建同构式 (朝着t+et转化).
由aex-lnx+lna≥0,得aex+lna≥lnx.结合对数恒等式有eln aex+lna≥lnx,所以eln a+x+lna≥lnx.在不等式的两边同时加上x,得eln a+x+(lna+x)≥x+lnx.这时可以令φ(x)=x+ex.因为φ(x)=x+ex在(0,+∞)上单调递增,所以由φ(x+lna)≥φ(lnx),得x+lna≥lnx,即lna≥lnx-x.
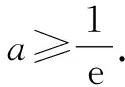
解法5:利用ex≥x+1放缩.
由aex≥lnx-lna,得eln aex≥lnx-lna,故ex+ln a≥lnx-lna.而ex+ln a≥x+lna+1,故只需x+lna+1≥lnx-lna即可,所以2lna≥lnx-x-1.
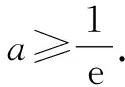
解法6:利用ex≥x+1,lnx≤x-1同时放缩[2].
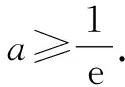
3 一题多思
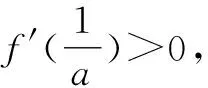
4 变式训练
(1)(2021年西湖区校级模拟)已知函数f(x)=mln(x+1)-3x-3,若不等式f(x)>mx-3ex在(0,+∞)上恒成立,则实数m的取值范围是( ).
A.[0,+∞) B.[3,+∞)
C.(-∞,3] D.(-∞,0]
(2)(2021年衡阳雁峰区期中试题)已知函数f(x)=ex-aln(ax-a)+a(a>0),若关于x的不等式f(x)>0恒成立,则实数a的取值范围是( ).
A.[0,e2] B.(0,e2) C.[1,e2] D.(1,e2)
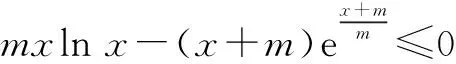
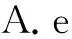
(4)(2021年沈阳一模第12题)已知函数f(x)=alnx-2x,若不等式f(x+1)>ax-2ex在x∈(0,+∞)上恒成立,则实数a的取值范围是( ).
A.a≤2 B.a≥2 C.a≤0 D.0≤a≤2
(5)(2021年鄂东南联盟测试第16题)已知x0是函数f(x)=x2ex-2+lnx-2的零点,则e2-x0+lnx0=.
(6)(2021年江淮十校联考第16题)已知实数α,β满足αeα=e3,β(lnβ-1)=e4,其中e是自然对数的底数,则α·β=.
5 归纳总结
如果等式或者不等式的两侧呈现同构特征,则可将相同的结构构造为一个函数,进而与函数的单调性建立联系,再比较大小或解不等式.
同构的应用:①指对各一边,参数是关键;②常用“母函数”,如f(x)=x·ex,f(x)=ex±x,寻找“亲戚函数”是关键;③信手拈来凑同构,凑常数、凑x、凑参数;④复合函数(“亲戚函数”)比大小,利用单调性求解.
