数形结合变视角 合理分类定乾坤
——2022年全国高考乙卷导数压轴题解法研究
2023-03-11易明交陈晓宁刘香杰
易明交 陈晓宁 刘香杰
⦿杭州师大附属阿克苏市高级中学
1 试题呈现
(2022年全国高考乙卷第21题)已知函数f(x)=ln(1+x)+axe-x.
(1)当a=1时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)若f(x)在区间(-1,0),(0,+∞)各恰有一个零点,求a的取值范围.
本题第(1)问考查函数在某点处的切线问题,利用导数的几何意义就可以解决.第(2)问考查的是函数在两个区间上的零点问题,解决函数零点问题的一种方法就是通过研究函数的单调性观察图象与x轴交点的个数,另一种是通过分离参数后探究两个函数图象交点的个数.
分析:(1)先求f′(x),f′(0)即为曲线在点(0,f(0))处切线的斜率,进而求出切线方程.
(2)求导,对a进行分类讨论,并对x∈(-1,0),x∈(0,+∞)分别研究.

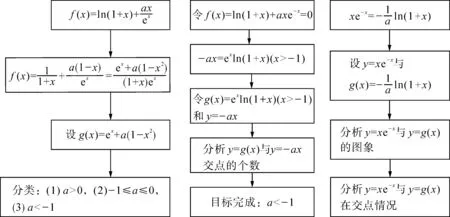
图1
2 试题解析
2.1 第(1)问详解
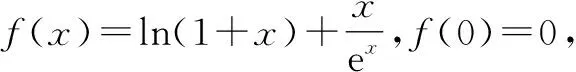
2.2 第(2)问详解
思路一:对参数合理分类,分步研究函数的零点情况.
解法1:因为f(x)=ln(1+x)+axe-x,所以
设g(x)=ex+a(1-x2),则g(0)=a+1.
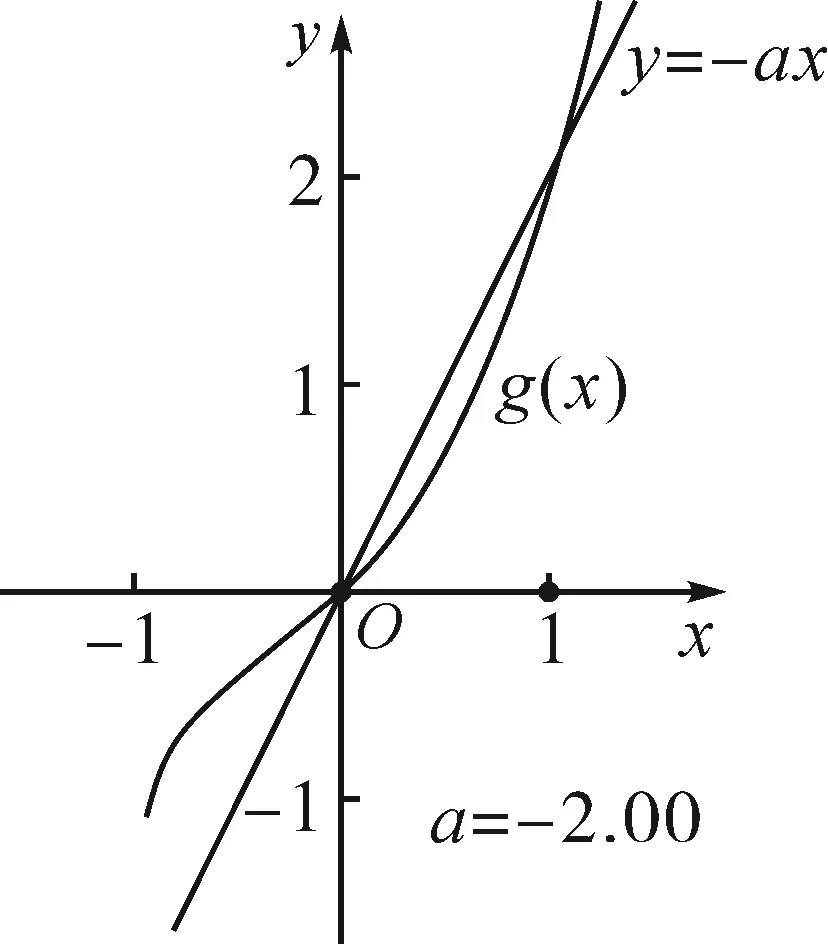
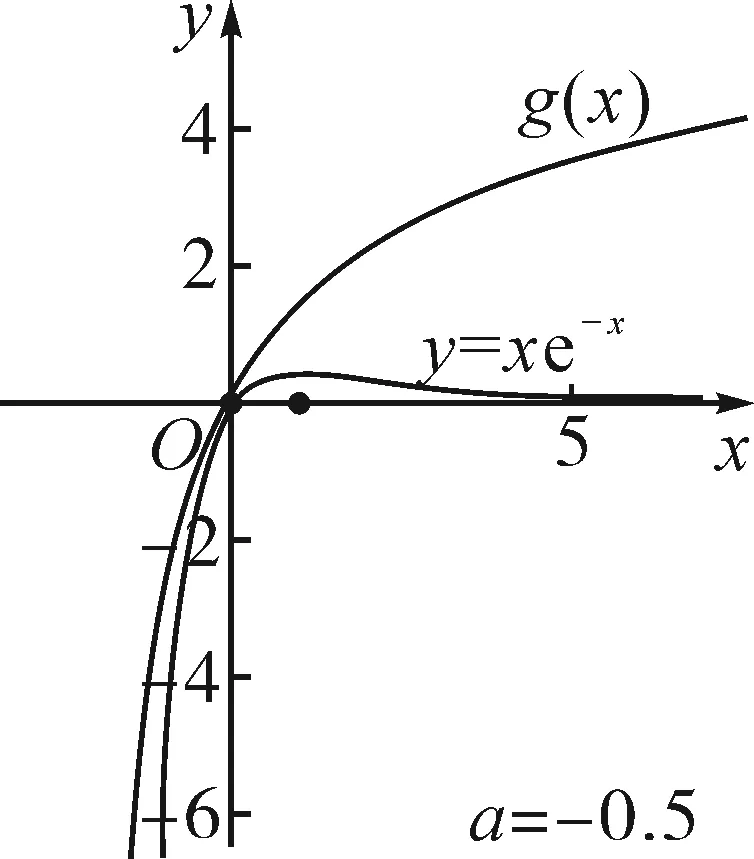
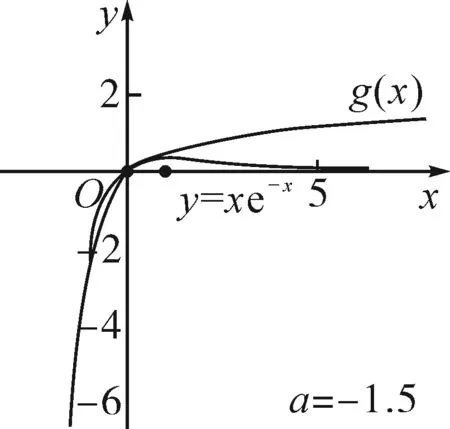
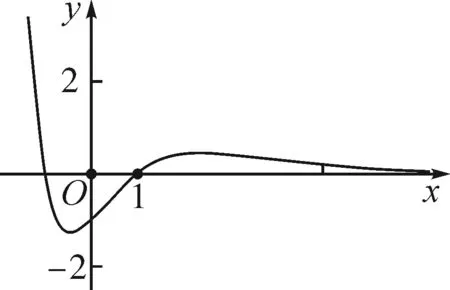
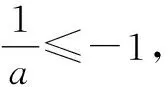
①若a>0,当x∈(-1,0)时,g(x)=ex+a(1-x2)>0,即f′(x)>0,所以f(x)在(-1,0)上单调递增,f(x) ②若-1≤a≤0,当x∈(0,+∞)时,g′(x)=ex-2ax>0,则g(x)在(0,+∞)上单调递增,从而g(x)>g(0)=a+1≥0,即f′(x)>0.所以f(x)在(0,+∞)上单调递增,f(x)>f(0)=0.故f(x)在(0,+∞)上没有零点,与题意矛盾. ③若a<-1,当x∈(0,+∞),g′(x)=ex-2ax>0,则g(x)在(0,+∞)上单调递增;又因为g(0)=a+1<0,g(1)=e>0,所以存在x0∈(0,1),使g(x0)=0,即f′(x0)=0.当x∈(0,x0)时,f′(x)<0,则f(x)单调递减;当x∈(x0,+∞)时,f′(x)>0,则f(x)单调递增.所以,当x∈(0,x0)时,f(x) 若a<-1,当x∈(-1,0)时,g(x)=ex+a(1-x2),g′(x)=ex-2ax. 图2 综上所述,a的取值范围为(-∞,-1). 思路二:利用参变半分离,研究图象的切线与直线之间的位置关系,确定零点个数. 解法2:由f(x)=ln(1+x)+axe-x=0,得-ax=exln(1+x)(x>-1). 令h′(x)=0,得x=0.当x∈(-1,0)时,h′(x)<0;当x∈(0,+∞)时,h′(x)>0. 所以h(x)min=h(0)=1,从而h(x)≥1在区间(-1,+∞)上恒成立. 所以g(x)在(-1,+∞)上单调递增.又g(0)=0,且g′(0)=1,则g(x)在x=0处的切线方程为y=x. 因为f(x)在区间(-1,0),(0,+∞)各恰有一个零点,也就是说g(x)与y=-ax在区间(-1,0),(0,+∞)各恰有一个交点,所以只需要-a>1,即a<-1.(如a=-1或-2时,如图3,4所示). 所以,a的取值范围为(-∞,-1). 图3 图4 点评:解法2的关键是分离参数构造出两个函数,分析g(x)的单调性,找出g(x)在点(0,0)处的切线,从而只需直线y=-ax的斜率大于1才能使直线与函数g(x)图象有两个交点. 思路三:利用参变全分离,准确作出函数的图象,然后上下移动直线,观察直线与函数交点个数即可. 令h(x)=(x2-1)ln(x+1)+x,则h′(x)=x[2ln(x+1)+1]. 当x>0时,h′(x)>0,则h(x)在(0,+∞)单调递增,所以h(x)>h(0)=0,从而g′(x)<0,故g(x)在(0,+∞)单调递减. 所以a<-1时,在(0,+∞)上y=a与y=g(x)的图象只有一个交点,因此f(x)在区间(0,+∞)恰有一个零点. 所以g(x)在(-1,x1)单调递增,在(x1,0)单调递减,从而g(x)max=g(x1). 又x→-1时,g(x)→-∞,且有 所以只有a<-1时,在(-1,0)上y=a与y=g(x)的图象只有一个交点,因此f(x)在区间(-1,0)恰有一个零点.(如a=-1或-2时,如图5,6所示). 综上所述,a的取值范围为(-∞,-1). 图5 思路四:对函数解析式合理变形,零点不发生变化. 解法4:对f(x)=ln(1+x)+axe-x两边同乘ex,得exf(x)=exln(x+1)+ax.令g(x)=exf(x),即g(x)=exln(x+1)+ax(x>-1),则g(0)=0,且 又x→-1时,g′(x)→+∞,所以存在x1∈(-1,x0),x2∈(0,-a),使g′(x1)=g′(x2)=0,且g(x)在(-1,x1)上单调递增,在(x1,x2)上单调递减,在(x2,+∞)上单调递增.又因为g(0)=0,所以g(x1)>0,g(x2)<0,于是存在x3∈(-1,0),x4∈(0,+∞),使g(x3)=g(x4)=0. 综上所述,a的取值范围为(-∞,-1). 解法5:设y=xe-x,则y′=e-x(1-x).所以,当-1 当a≥0时,f(x)在(-1,1)上单调递增,且f(0)=0,所以f(x)在(-1,0)上无零点,这与题意矛盾. 故a的取值范围为(-∞,-1). 图7 图8 当a≥0时,x∈(-1,1)时,f′(x)>0,则f(x)在(-1,1)上单调递增.又f(0)=0,则当x∈(-1,0)时f(x)<0,所以f(x)在(-1,0)上不存在零点. 图9 综上所述,a的取值范围为(-∞,-1). 链接1(2022年浙江温岭中学模拟题)已知函数f(x)=alnx+e-x(x-1). (1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程; (2)证明:当a≥0时,f(x)有且只有一个零点; (3)若f(x)在区间(0,1),(1,+∞)各恰有一个零点,求a的取值范围. 链接2(2018年全国高考理科第21题)已知函数f(x)=ex-ax2. (1)若a=1,证明:当x≥0时,f(x)≥1; (2)若f(x)在(0,+∞)只有一个零点,求a的值. 2022年全国高考乙卷第21题在考查导数的基本运算法则、基本性质等知识点的同时,考查学生的运算求解、数学分析等关键能力以及转化与化归、数形结合等思想方法,较好地考查学生学科核心素养.题目的求解,需要学生有较强的逻辑思维转换能力与代数计算能力.不难发现,上述解法2和解法3的解答过程都围绕“分参”展开,归纳起来无外乎两类:一类是等式关系转化为参数与函数图象的交点问题;另一类就是函数的切线与函数图象的交点问题.通过对分离参数法的再思考,在解决可分参的问题时,指导学生抓住问题的本质,掌握通性、通法,让学生可以触类旁通、事半功倍,达成练一题、学一法、会一类、通一片的效果.在解题教学中,教师要有意识地引导学生探究问题的本质,注重解题过程,从繁杂的试题以及多变的解法中,追根溯源,探寻不变的本质,从而真正达到事半功倍的效果.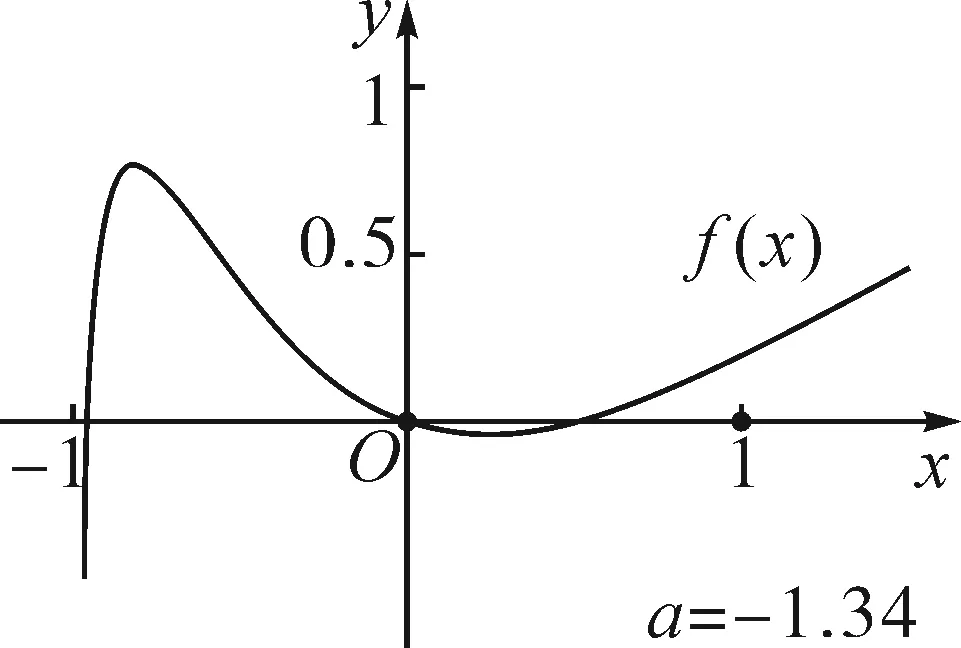

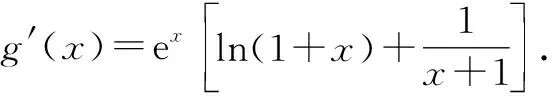
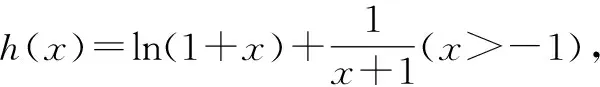
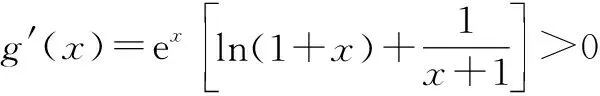
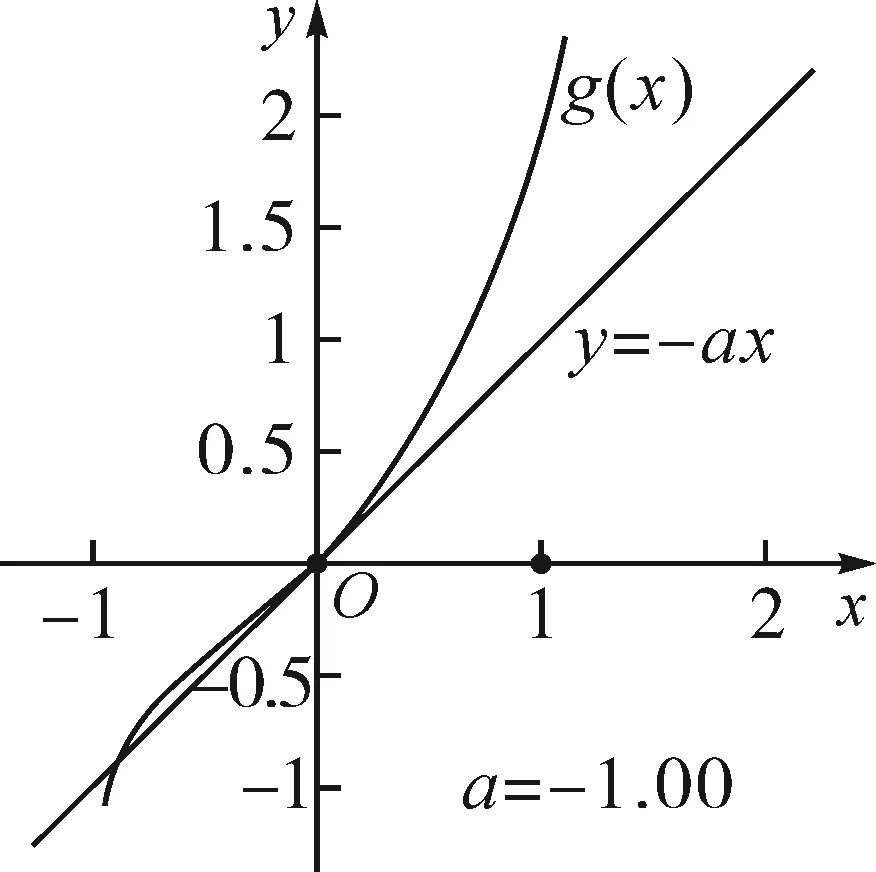
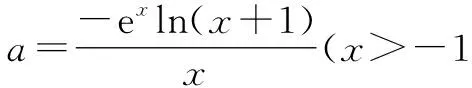
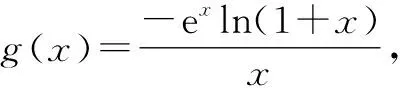
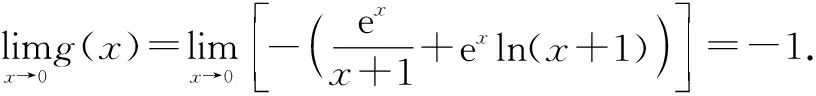
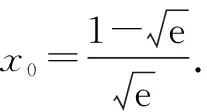
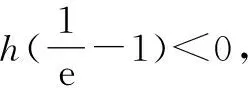
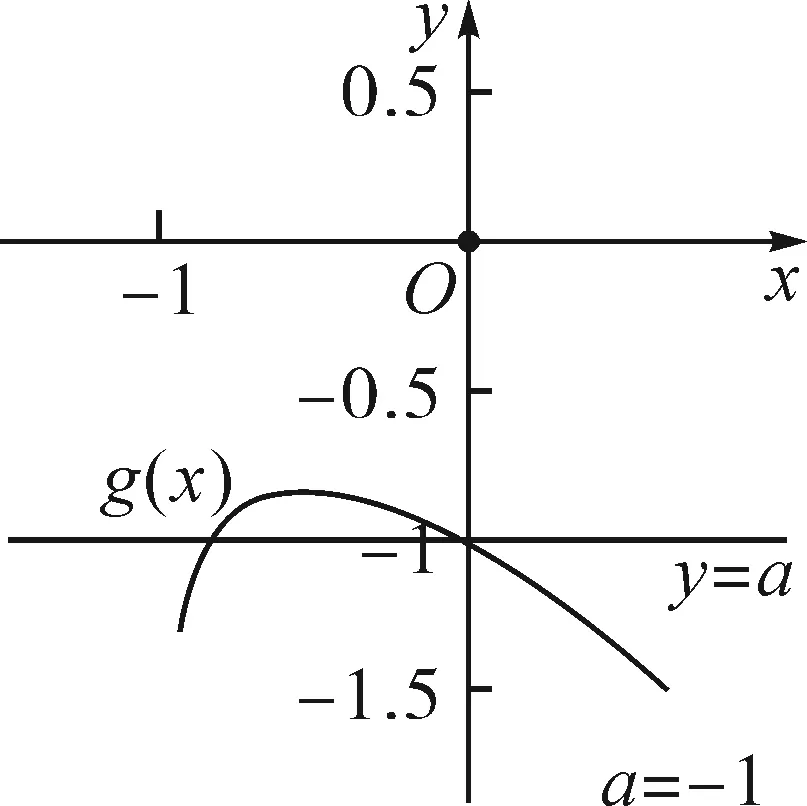
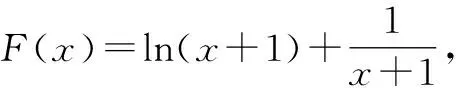
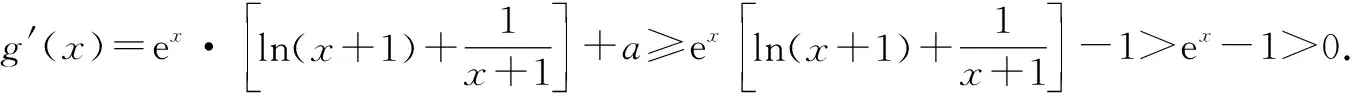
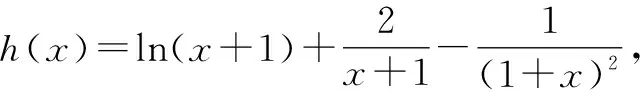
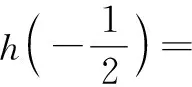
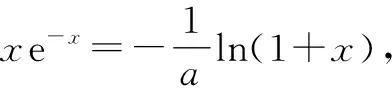
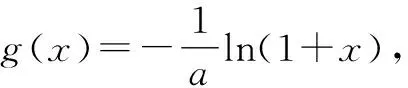
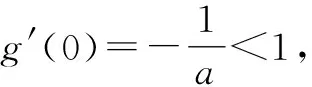
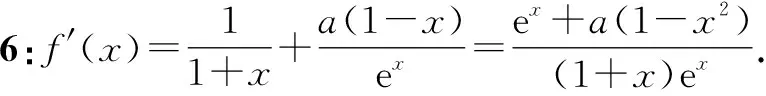
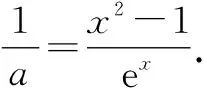

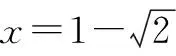
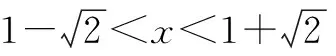
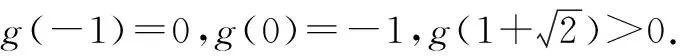
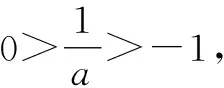
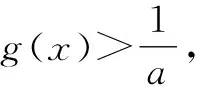
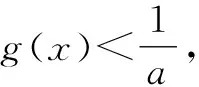
3 链接高考
