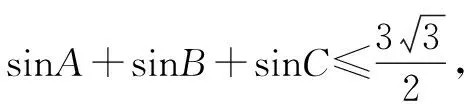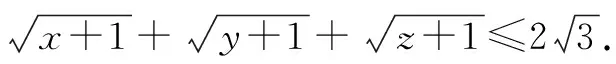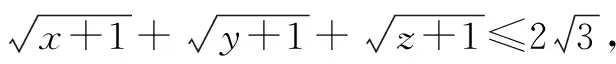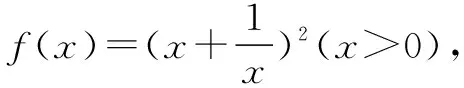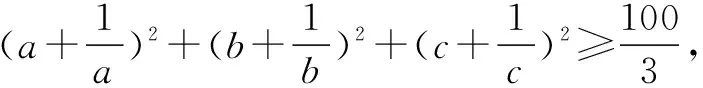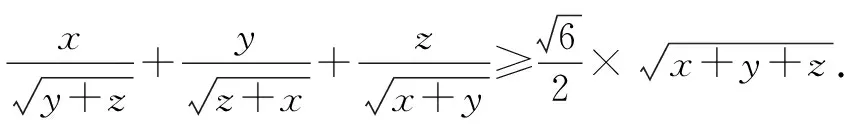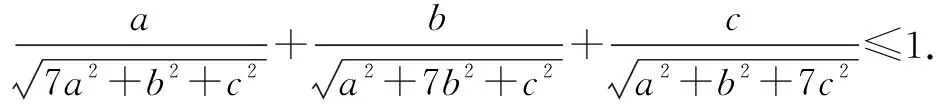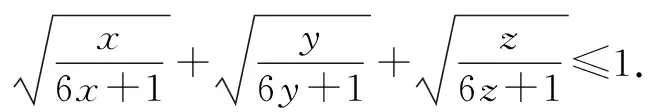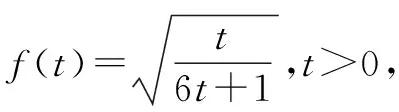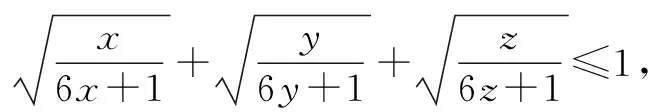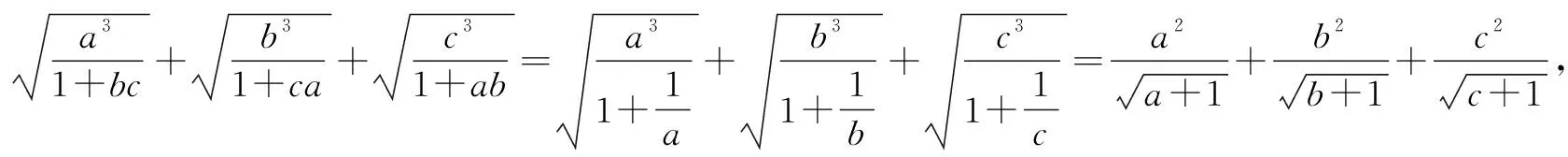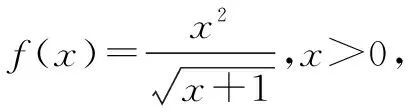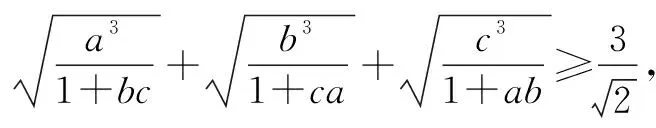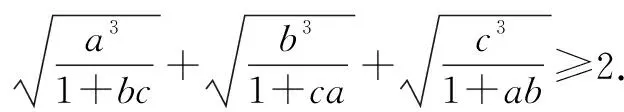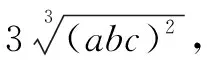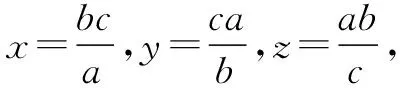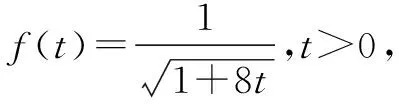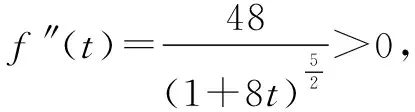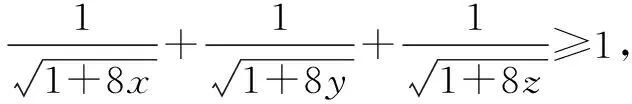琴生不等式在不等式证明中的应用

林国红

(广东省佛山市乐从中学 528315)

不等式的证明方法众多，灵活多变，技巧性较强，其中构造函数是证明不等式的有效手段之一，利用构造函数法来证明不等式实质是函数性质的应用，其关键在于根据题设条件的特征，构造一个恰当的函数.琴生不等式是函数凸凹性的应用，在中学数学有着广泛应用，特别是在竞赛与自主招生中应用较多.如果能够根据题设、结论的结构特征，巧妙变换，灵活选用琴生不等式往往解题过程简洁明快，能起到事半功倍的效果，堪称解题“利器”.

下面通过几个例子说明琴生不等式在不等式证明中的应用.

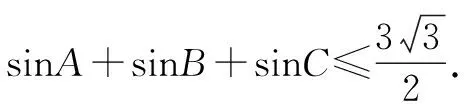
证明设f(x)=sinx(0

f′(x)=cosx，f″(x)=-sinx<0.

从而函数f(x)在(0,π)是上凸函数.

由琴生不等式，可得

从而函数f(t)在(0,+∞)是上凸函数.

由琴生不等式，可得

从而函数f(x)在(0,+∞)是下凸函数.

由琴生不等式，可得

从而函数f(t)在(0,1)是下凸函数.

由琴生不等式，可得

所以原不等式得证.

不妨设a2+b2+c2=1，记x=a2,y=b2,z=c2，则x+y+z=1.

从而函数f(t)在(0,+∞)是上凸函数.

由琴生不等式，可得

所以原不等式得证.

所以函数f(x)在区间(0,+∞)是下凸函数.

由琴生不等式与均值不等式有：

当且仅当a=b=c=1时，等号成立.

原不等式可化为

所以只需要证明：

所以函数f(t)在(0,+∞)是单调递减.

所以函数f(t)在(0,+∞)是下凸函数.

再由琴生不等式与均值不等式得：

当且仅当x=y=z=1时，等号成立.

所以原不等式得证，当且仅当a=b=c=1时，等号成立.

从以上几例不难发现，通过构造凸函数，利用琴生不等式证明不等式，能降低思维强度，简化推理过程，具有直观、简捷、明快的特点，证明思路新颖独到，充分体现了琴生不等式的魅力.