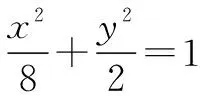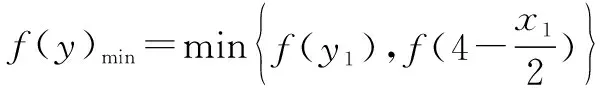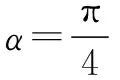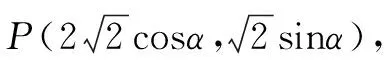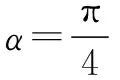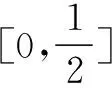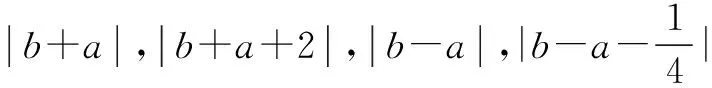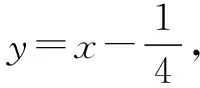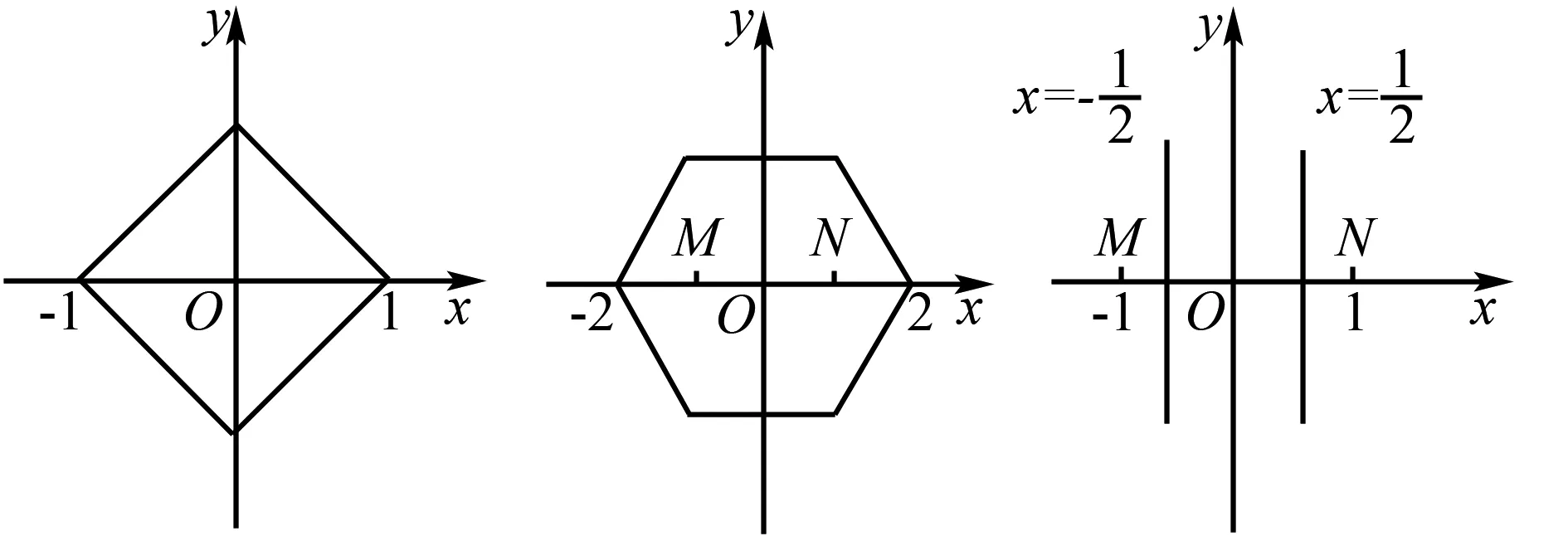曼哈顿距离及其应用
2022-12-10张君
张 君
(四川省温江中学 611130)
1 曼哈顿距离
设P(x1,y1),Q(x2,y2)为平面上两点,则定义|x2-x1|+|y2-y1|为“折线距离”“直角距离”或“曼哈顿距离”,记作d(P,Q)=|x2-x1|+|y2-y1|.
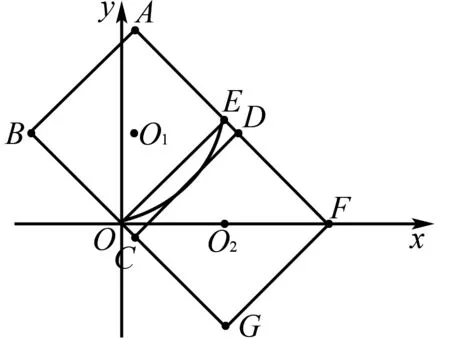
曼哈顿距离的几何意义:如图1,点P(x1,y1)在以Q(x2,y2)为中心的正方形(对角线平行于坐标轴)上,点P到点Q的曼哈顿距离为正方形对角线长的一半.

图1
2 两个重要结论
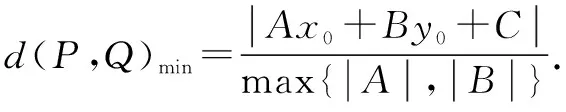
证明当|A|>|B|时,则有
d(P,Q)=|x-x0|+|y-y0|

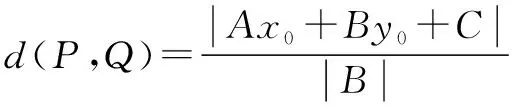
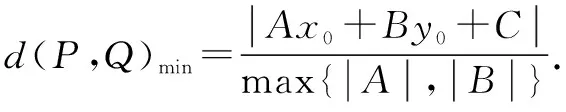
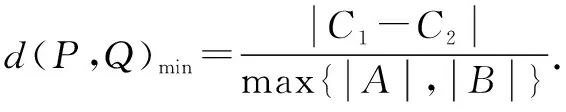
证明设P(x0,y0),则Ax0+By0=-C1.利用结论1可知
3 曼哈顿距离的应用
例1(2006年福建卷理科)对于直角坐标平面内的任意两点A(x1,y1)和B(x2,y2),定义它们之间的一种“距离”:||AB||=|x2-x1|+|y2-y1|.给出下面三个命题:
①若点C在线段AB上,则||AC||+||CB||=||AB||;
②在△ABC中,若∠C=90°,则||AC||2+||CB||2=||AB||2;
③在△ABC中,||AC||+||CB||>||AB||.
其中真命题的个数为( ).
A.0 B.1 C.2 D.3
解析可以验证本题中定义的距离||AB||=|x2-x1|+|y2-y1|符合距离公理的三条规则:非负性和对称性容易验证,对于三角形不等式,设C(x0,y0),有||AC||+||CB||=|x0-x1|+|y0-y1|+|x2-x0|+|y2-y0|≥|(x0-x1)+(x2-x0)|+|(y0-y1)+(y2-y0)|=|x2-x1|+|y2-y1|=||AB||,
当且仅当x1≤x0≤x2且y1≤y0≤y2时,等号成立.
于是可知,①正确,③错误;②中结论是欧氏距离下的勾股定理,举特例发现在本题的“距离”下将不再成立.
综上,真命题只有①,故选B.
例2 (2014年福建卷文科)在平面直角坐标系中,两点P1(x1,y1),P2(x2,y2)间的“L-距离”定义为‖P1P2‖=|x1-x2|+|y1-y2|,则平面内与x轴上两个不同的定点F1,F2的“L-距离”之和等于定值(大于‖F1F2‖)的点的轨迹可以是( ).
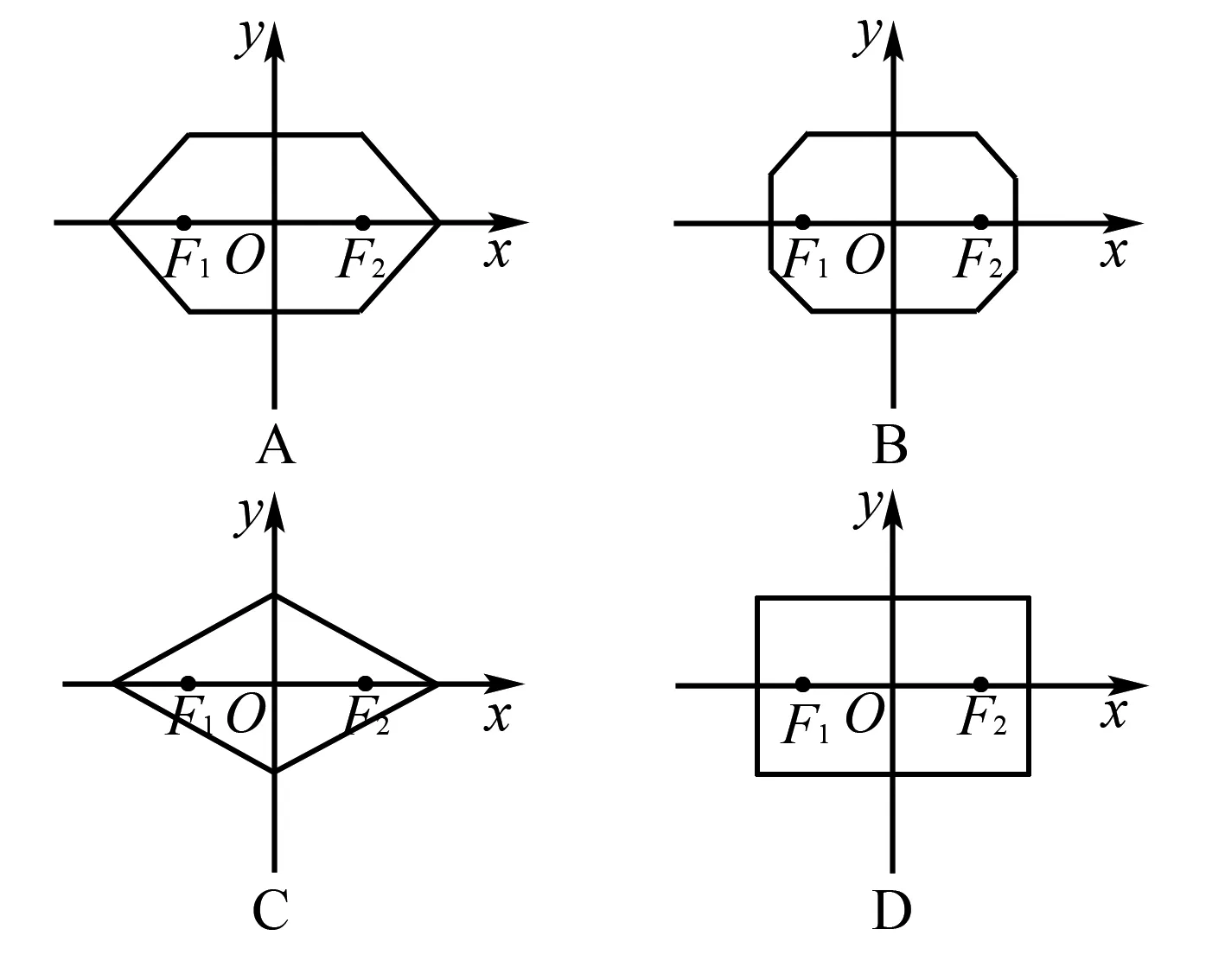
解析设F1(-c,0),F2(c,0),动点M(x,y)到定点F1,F2的“L-距离”之和等于2m(m>c>0).则‖MF1‖+‖MF2‖=2m.
即|x+c|+|x-c|+2|y|=2m.
对x分类讨论如下:
当x≤-c时,有-x-c+c-x+2|y|=2m,x-|y|+m=0(该式蕴含x≥-m),即x±y+m=0;
当-c 当x≥c时,有x+c+x-c+2|y|=2m,x+|y|-m=0(该式蕴含x≤m),即x±y-m=0. 画出以上三种情形的图象,可知正确选项为A. 解析由结论1可得 解法1(主元函数法)以点Q的纵坐标为主变量y,则|x2-x1|+|y2-y1|=|8-2y2-x1|+|y2-y1|,令f(y)=|8-2y-x1|+|y-y1|,则该函数的图象是一条线段和两条射线组成的开口向上的“楔形”. 由图象可知其最小值只能在图象连接点(即在这两个一次绝对值函数的两个零点)处取得. 问题转化为求椭圆上的点P到直线x+2y-8=0距离的最小值. 所以f(y)min=2. 所以d(P,Q)min=2. 例5 (2018年浙江联考)已知函数f(x)=|x+a|+|x2+b|,x∈[0,1],设f(x)的最大值为M,若M的最小值为1,则a的值可以是( ). 解法1因为|x+a|+|x2+b|≥|x2+x+a+b|,|x+a|+|x2+b|≥|x2-x-a+b|, 4.2.1 建立健全医疗纠纷机制提高从医信心。针对医患关系紧张对医学生从业信心的影响,需要多角度进行改进,要不断建立健全医疗纠纷机制,为解决医患关系找到合理的路径,通过有效的途径解决医疗过程产生的纠纷,缓解医患矛盾,提高从医者的信心。 故M≥|x2+x+a+b|,M≥|x2-x-a+b|. 由于函数y=x2+x+a+b在[0,1]上单调递增,所以|x2+x+a+b|的最大值在端点处取到,其最大值为max{|b+a|,|2+b+a|}; 解法2题中f(x)=|x+a|+|x2+b|可视为P(x,x2)和Q(-a,-b)两点之间的曼哈顿距离,其最大值M表示以Q(-a,-b)为中心,恰能把整段曲线(y=x2,x∈[0,1])包住的正方形对应的曼哈顿距离.M的最小值为1,这就意味着,以Q为中心且最小对角线长为2的正方形可以包住整段曲线.移动正方形可以得到中心Q的轨迹,其对应横坐标相反数的取值范围即是a的取值范围. 图2 易得Q2(1,0). 例6 (原创题)在平面直角坐标系xOy中,定义d(P,Q)=|x2-x1|+|y2-y1|为P(x1,y1),Q(x2,y2)两点之间的“折线距离”.在这个定义下,给出下列命题:①到原点的“折线距离”等于1的点的集合是一个正方形;②到原点的“折线距离”等于1的点的集合是一个圆;③到两点的“折线距离”之和为4的点的集合是面积为6的六边形;④到两点的“折线距离”之差为1的点的集合是两条平行线. 其中正确的命题是____. 解析答案是①③④.设O为原点,P(x,y),则d(O,P)=|x-0|+|y-0|=1,即点P的轨迹方程是|x|+|y|=1,这是四条线段围成的正方形(图3),故①正确,②错误. 图3 图4 图5 对于③,由定义得点P(x,y)满足|x-1|+|x+1|+2|y|=4,通过分段画图可知其图象是边长为2的正六边形(图4),其面积为6,故③正确. 例7 (多选题)在平面直角坐标系xOy中,定义d(P,Q)=|x2-x1|+|y2-y1|为P(x1,y1),Q(x2,y2)两点之间的“哈曼顿距离”,则下列说法正确( ). A.若点C在线段AB上,则有d(A,C)+d(C,B)=d(A,B) B.若A,B,C是三角形的三个顶点,则有d(A,C)+d(C,B)>d(A,B) D.若O为坐标原点,点P满足d(O,P)=1,则点P所形成图形的面积为2 解析若C在线段AB上,设点C的坐标为(x0,y0),则x0在x1,x2之间,y0在y1,y2之间.所以d(A,C)+d(C,B)=|x0-x1|+|y0-y1|+|x2-x0|+|y2-y0|=|x2-x1|+|y2-y1|=d(A,B),故A正确. 在△ABC中d(A,C)+d(C,B)=|x0-x1|+|y0-y1|+|x2-x0|+|y2-y0|≥|(x0-x1)+(x2-x0)|+|(y0-y1)+(y2-y0)|=|x2-x1|+|y2-y1|=d(A,B),故B选项错误.