“嫦娥奔月”模型问题分类解析

李秀元

(湖北省武穴市实验高级中学 435400)

2020年12月17日，嫦娥五号返回器携月球样品顺利安全着陆，标志着我国探月工程取得了阶段性胜利，为进一步求索寰宇开创了新的篇章.在“圆与方程”一章里，有一道精典习题，构图形如“嫦娥奔月”完美结构，让我们也有了在纸上对圆一探究竟的冲动.

1 “嫦娥奔月”模型

已知直线l与圆C相离，过直线l上任意一点P，作圆C的两条切线，切点分别为A，B，如图1所示.圆C犹如一轮圆月，直线l上任意点P犹如嫦娥上下翻飞，两条切线犹如其伸出的双臂，状如飞天揽月的构图，给人以无穷遐想，我们将其界定为“嫦娥奔月”模型.

图1

2 探索“嫦娥奔月”模型

“嫦娥奔月”模型本质上就是直线与圆相离，它究竟能解决哪些问题呢？我们以例题的形式，循序渐进地带领大家完成七大探究工程.

2.1 切线长的最小值问题

例1已知点P是直线l：x+3y-12=0上的一点，过点P作圆N：(x-2)2+y2=1的切线，切点为A，求切线段|PA|的最小值.

分析由于直线l与圆N相离，点P移动切点A随之移动，感觉当点P离圆N最近时，所作切线取得最小值.将这种感觉数量化，实质上就是将两个动点间的距离，动中取定，转换成数学常见最值问题.

图2

所以切线段|PA|的最小值为3.

小结借助勾股定理，利用定圆半径，将两动点间的距离转化成定点(圆心)与直线上动点间的距离，进而利用点到直线的距离公式，完成计算.

2.2 切点四边形面积的最小值问题

我们把圆外一点、两个切点及圆心这4点围成的四边形称为切点四边形.

例2已知圆M：x2+(y-2)2=1，直线l：x-3y=0，点P在直线l上，过点P作圆的切线PA，PB，切点为A，B，如图3.

图3

(1)若∠APB=60°，求点P的坐标；

(2)求四边形PAMB面积的最小值及此时点P的坐标.

解析因为点P在直线x-3y=0上，设P(3m,m).

(1)由已知，得圆心M(0,2)，半径r=1.

又∠APB=60°，所以|MP|=2|MA|=2.

(2)显然，四边形PAMB面积等于Rt△PAM面积的2倍，即|PA|×|AM|.因此，当|PA|取最小值时，四边形PAMB面积最小.

因为PA2=PM2-MA2=PM2-1，

所以当|PM|最小时，|PA|取最小值.

2.3 切点弦的最小值问题

连接圆的两个切点所得线段称为圆的切点弦.

例3若点P为直线x-y+4=0上的一个动点，从点P引圆C：x2+y2-4x=0的两条切线PM，PN，切点为M，N，求弦|MN|的最小值.

分析点P离圆C由远及近，又由近及远，点P对圆C的张角，随点P的移动先增大后减小，猜测当点P离圆C最近时，切点弦最短.

解析由x2+y2-4x=0，得(x-2)2+y2=4.

从而C(2,0).如图4，连接PC，则PC⊥MN，且PC平分MN，设交点为Q.

图4

要使|MN|最小，则|MQ|也最小.

由直角三角射影定理，得MC2=|CQ|×|CP|.

可以看到，圆的切点四边形面积和切点弦长度问题最终都转化为圆的切线长问题，且当圆心与点P的连线垂直于直线时，分别取得最小值.

2.4 定点对应的切点弦方程问题

例4 已知⊙M：x2+y2-2x-2y-2=0，直线l：2x+y+2=0，P为l上的动点.过点P作⊙M的切线PA，PB，切点为A，B，当|PM|·|AB|最小时，直线AB的方程为____.

分析如图5所示，显然有PM⊥AB，因此|PM|·|AB|表示四边形PAMB的面积，也即△PAM面积的2倍.要使△PAM面积最小，则|PA|需取得最小值，由例2可知，此时PM⊥l，只需要求出点P的坐标即可.

图5

即点P坐标为(-1,0).

以PM为直径的圆的方程为(x+1)(x-1)+y(y-1)=0.即x2+y2-y-1=0.

即直线AB的方程为2x+y+1=0.

归纳一般地，点P(x0,y0)为圆(x-a)2+(y-b)2=r2外一点，则过点P所作切线，切点弦方程为(x-a)(x0-a)+(y-b)(y0-b)=r2.

2.5 定直线上动点对应的切点弦过定点问题

(1)若直线l与圆C相交，求k的取值范围；

(2)若k=1，点P是直线l上一个动点，过点P作圆C的两条切线PM，PN，切点分别为M，N，证明：直线MN恒过定点.

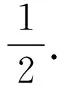
又点P(x0,y0)在直线y=x-1上，故y0=x0-1.

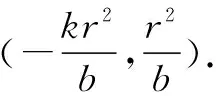
2.6 定直线上动点对应的切点弦中点的轨迹方程

例6 已知A(-4,0)，B(0,4)，圆O：x2+y2=4.过直线AB上任一点P作圆O的两条切线，切点分别为C,D，M为线段CD的中点，求|AM|的最大值.

分析要求|AM|的最大值，先得知道动点M的轨迹是什么图形，这样才能将两点间的距离问题转化成定点与定曲线上动点间的距离.

解析设M(x,y)，直线AB的方程为y=x+4，由例5知，直线CD恒过定点N(-1,1).

如图6，显然有OM⊥CD，即OM⊥MN.

图6

2.7 定直线上动点对应的切点四边形外接圆过定点问题

例7已知圆M：x2+(y-2)2=1，点P是直线l：x+2y=0上的一个动点.过点P作圆M的切线PA,PB，切点为A,B.

(2)若△PAM的外接圆为圆N，试问：当点P运动时，圆N是否过除点M外的定点？若存在，求出定点的坐标；若不存在，请说明理由.

(2)设P(-2b,b)，△PAM的外接圆N是以PM为直径的圆，其方程为

整理,得(2x-y+2)b+(x2+y2-2)=0.

图7