浅谈均值不等式的应用
2018-02-22吉林师范大学王昱行
数学大世界 2018年35期
吉林师范大学 王昱行
一、利用均值不等式证明不等式
利用均值不等式证明不等式时,应注意以下几点:
2.如果式子不具备均值不等式的特点,那么需要通过加减项的方法拼凑成可用均值不等式的形式。
3.灵活应用均值不等式的变形形式,注意均值不等式的变形应用。
例1 已知a,b,c∈R+,且a+b+c=1。
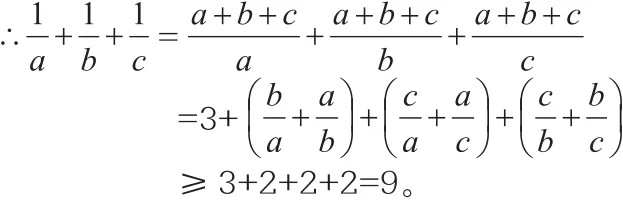
二、利用均值不等式求最值
在利用均值不等式求最值时,必须同时满足以下三个条件:一证、二定、三相等。即:
①x,y都是正数。
②积xy(或和x+y)为常数(有时需要通过“配凑、分拆”凑出定值)。
③x与y必须能够相等(即等号能够取到)。
特别地,当条件中等号在此不成立时,此时不能运用均值不等式来解题,而是应该应用函数的单调性来求最值。
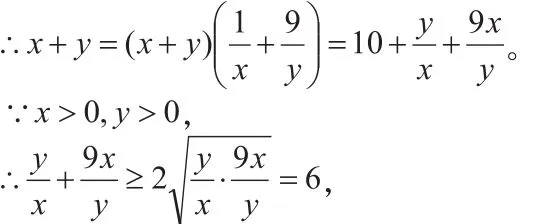
三、利用均值不等式比较实数大小
1.注意均值不等式成立的前提条件。
2.注意“1”的代换。
3.合理配组,反复应用均值不等式。
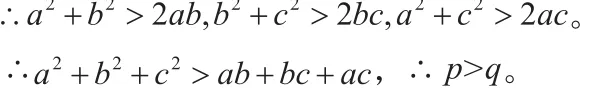
本文列举了常用的有关均值不等式的三种题型,对于已给定的条件,具体用哪种方法求解,需要首先分析一下给定条件的结构和特点,然后再考虑选用什么方法比较妥当。因此,在解决相关问题时,要多观察,多总结。
