架等时圆之桥 铺滑行时间问题求解之路
2022-12-10王伟民
王伟民
(安徽省太和县宫集镇中心学校 236652)
由竖直平面内圆周的最顶端(即该圆竖直直径的上端点),从静止开始沿各个倾角不同光滑斜面自由下滑的物体,滑行到斜面与圆另一个交点所用的时间相等,都等于物体从圆周的最顶端开始作初速度为零的自由落体运动过程中,自由下落这个圆直径高度所用的时间,该圆被称之为等时圆.在求解与物体沿光滑斜面(或光滑细杆)自由下滑时间有关的问题时,通过添加辅助等时圆的方法进行求解,往往可以起到事半功倍的作用.
例1 如图1所示,斜面OB与水平面OA的夹角为α,C是斜面上的一点,P是过C点竖直线上C上方的一点,PC=h,某光滑细杆PE过P点,其底端放在斜面上,一小环套在细杆上由P点静止释放,求小环沿光滑细杆滑落到斜面的最短时间?

图1 图2
我们先用解析法对该问题进行求解.

因为小环在光滑细杆上下滑过程中的加速度为gcosθ,所以,小环在光滑细杆上由P点静止释放,下滑到斜面上的E点所用时间的平方t2为:
将t2视为θ的函数并对θ进行求导可得:





再用增添辅助等时圆的方法对例题1给出的问题进行求解.
解法二如图3所示,作过点P、圆心在竖直线PC上并且和OB相切的圆⊙I,设切点为H,显然,满足条件的圆不仅存在,而且是唯一的.图3中,OB上除了H点之外的其余所有各点都在⊙I外,以图3中的E点为其余各点的代表进行分析.由等时圆的性质可知,小环分别沿光滑细杆PE和PH由P点静止释放自由滑行时,在细杆PG段滑行的时间与在细杆PH段滑行的时间相等,所以,小环在细杆PH段滑行的时间一定小于它在细杆PE段滑行所用的时间,因此,在过P点倾角不同的各细杆中,小环唯有沿过切点H的细杆滑行所用的时间最短.

图3

比较以上两种不同的解法可以发现,运用解析法求解问题的答案时,解题过程冗长繁杂,解答过程的大部分内容是数学推理,显得晦涩难懂,而运用增添辅助等时圆的方法,求解小环沿光滑细杆滑行的最短时间,物理味道十足,解题过程直观易懂,简单明了.
我们再看将上面例题1物理情景中的直斜面更改为曲面之后,能否再用类似的方法来进行求解.
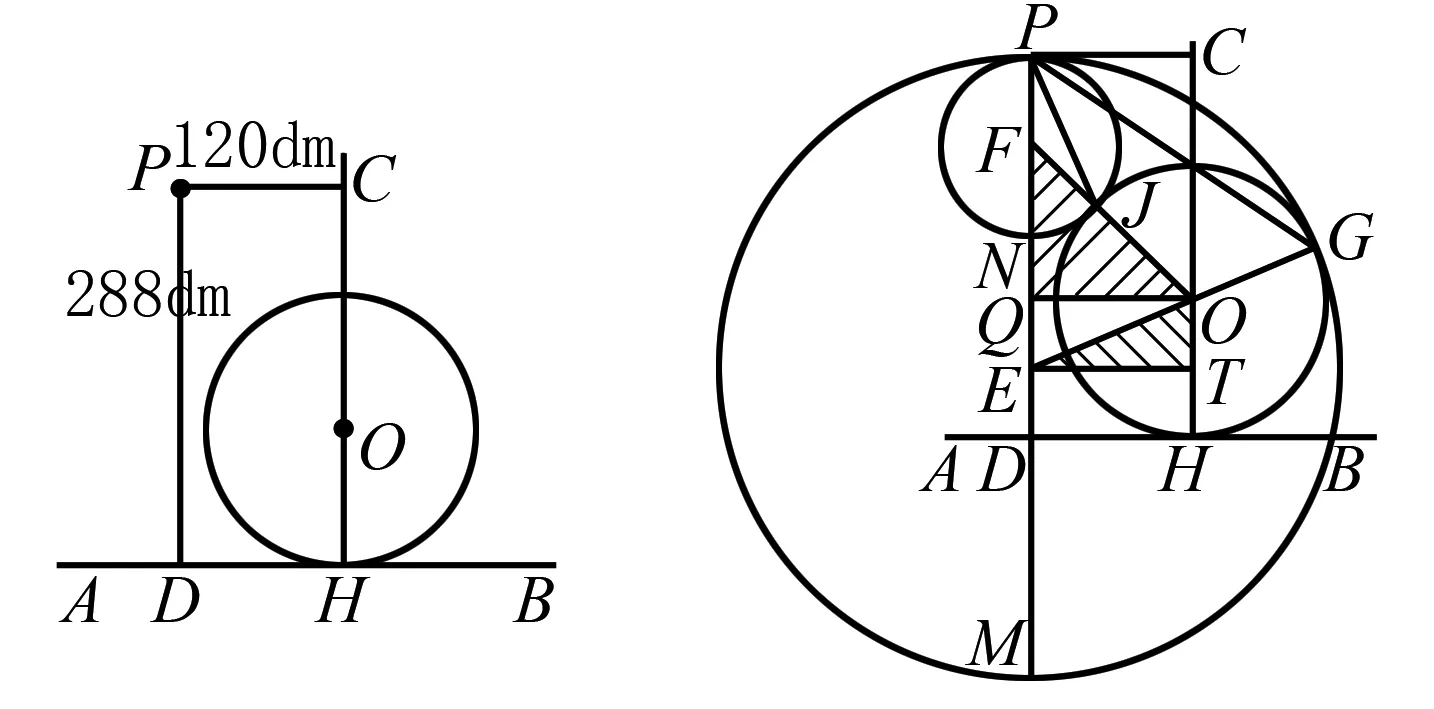
例2 如图4所示,半径为25m的圆环圆心为O,放在水平地面上,圆环所在的平面竖直,P点是圆环平面内的一点,它到该圆竖直直径和水平地面的距离分别为8m和34m,足够长的光滑细杆一端固定在P点,并且可以在圆环所在的竖直平面内任意转动,一小环套在细杆上由P点静止释放,求小环沿细杆滑到圆环上需要的最短时间?(取g=10m/s2)

图4 图5
分析如图5所示,作过点P、圆心在过P点的竖直线PD上,并且与⊙O相内切的⊙I,设切点为F,PM是过点P的另外一条往右下方倾斜的任意线段(M点在⊙O的圆周上),交⊙I于N,将PM和PF分别视为光滑细杆,由等时圆的性质可知,小环分别在两个光滑细杆上的PN段和PF段滑行的时间相等,都等于小环从P开始作自由落体运动PG距离(即⊙I的直径)所用的时间,所以,小环在两细杆上由P分别滑行到⊙O的圆周所用的时间tPF和tPM相比,有tPF 解析因为相切两圆的连心线过切点,所以O、I、F三点共线,设⊙I的半径为r,易知PE=PD-ED=9m,所以IE=r-9(单位m,下同),因为OI=25-r,所以,在Rt△OEI中根据勾股定理可以建立如下方程: (r-9)2+82=(25-r)2,解得:r=15, 所以,小环沿细杆由P滑行至F所用的时间为: 实际上,对例题2给出的这个求解小环沿细杆滑行的最短时间问题,我们也可以仿照例题1的解法一,建立合适的平面直角坐标系之后,确定出⊙O的方程,进而利用解析法导出小环在不同倾角滑杆上由P点滑行到⊙O的圆周上时,所需时间与其他参数的函数关系式,再利用求导的方法确定问题的答案,但这样解决问题的过程将会非常的麻烦,远不如增添辅助等时圆的方法求解简单. 例3 如图7所示,半径为104dm的圆环圆心为O,放在水平地面上,P点是竖直圆环平面内的一点,它到水平面和圆环竖直直径的距离分别是288dm和120dm,在P点和⊙O圆周上多点之间拉很多根绷紧的光滑金属丝,让套在金属丝上的小环在各金属丝上由P点静止释放,试确定小环在各段金属丝上滑行时间的取值范围?(取g=10m/s2,结果可以保留根号) 图6 图7 分析作出过点P,圆心在过P的竖直线PD上,与⊙O分别内切和外切的两圆⊙E和⊙F,如图7所示,切点分别是G和J,由等时圆的性质可知,在P点与⊙O上各点相连的金属丝中,小环在光滑金属丝PG上滑行的时间最长,最长时间等于小环在空间内从P点静止释放,自由下落⊙E的直径PM所用的时间;小环在光滑金属丝PJ上滑行的时间最短,最短时间等于小环在空间内从P点静止释放,自由下落⊙F的直径PN所用的时间.根据题目给出的已知条件,分别在Rt△OET和Rt△OQF中根据勾股定理列出两个以⊙E和⊙F半径为未知数的方程,可以确定⊙E和⊙F的半径分别,进而可以确定问题的答案. 解析设⊙E和⊙F的半径分别为R和r,在Rt△OET中: PN=PD-QD=184dm, 所以OT=QE=R-184(单位dm,下同),EO=R-104, 由勾股定理可得 (R-104)2=1202+(R-184)2,解得:R=234. 在Rt△OQF中: FQ=184-r,FO=104+r,OQ=120, 由勾股定理可得 (r+104)2=1202+(184-r)2,解得r=65. 等时圆的性质是运动学板块的一条重要规律,在解决物体于光滑斜面或滑杆上滑行时间等相关问题时,如果添加合适的等时圆,并以等时圆为桥梁,将有关物理量巧妙联系,往往可以给问题的解决带来很大的方便.