2019年高考江苏卷第12题的四种解法

蒋习文

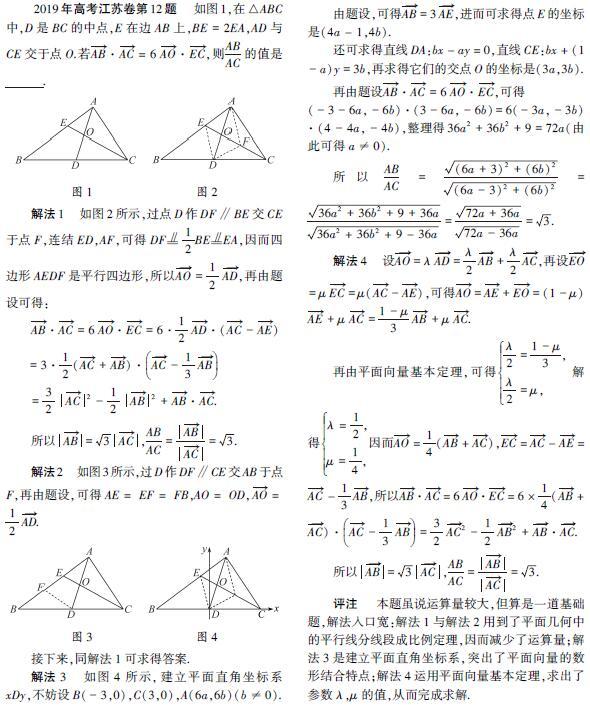
2019年高考江苏卷第12题 如图1，在△ABC中，D是BC的中点，E在边AB上，BE=2EA，AD与CE交于点O.若AB·AC=6AO·EC，则ABAC的值是

.

解法1 如图2所示，过点D作DF∥BE交CE于点F，连结ED，AF，可得DF瘙 綊 12BE瘙 綊 EA，因而四边形AEDF是平行四边形，所以AO=12AD，再由题设可得：

AB·AC=6AO·EC=6·12AD·（AC-AE）

=3·12（AC+AB）·AC-13AB

=32AC2-12AB2+AB·AC.

所以AB=3AC，ABAC=ABAC=3.

解法2 如图3所示，过D作DF∥CE交AB于点F，再由题设，可得AE=EF=FB，AO=OD，AO=12AD.

接下来，同解法1可求得答案.

解法3 如图4所示，建立平面直角坐标系xDy，不妨设B（-3，0），C（3，0），A（6a，6b）（b≠0）.

由题设，可得AB=3AE，进而可求得点E的坐标是（4a-1，4b）.

还可求得直线DA：bx-ay=0，直线CE：bx+（1-a）y=3b，再求得它们的交点O的坐标是（3a，3b）.

再由题设AB·AC=6AO·EC，可得

（-3-6a，-6b）·（3-6a，-6b）=6（-3a，-3b）·（4-4a，-4b），整理得36a2+36b2+9=72a（由此可得a≠0）.

所以ABAC=（6a+3）2+（6b）2（6a-3）2+（6b）2=36a2+36b2+9+36a36a2+36b2+9-36a=72a+36a72a-36a=3.

解法4 设AO=λAD=λ2AB+λ2AC，再设EO=μEC=μ（AC-AE），可得AO=AE+EO=（1-μ）AE+μAC=1-μ3AB+μAC.

再由平面向量基本定理，可得λ2=1-μ3，

λ2=μ， 解得λ=12，

μ=14，因而AO=14（AB+AC），EC=AC-AE=AC-13AB，所以AB·AC=6AO·EC=6×14（AB+AC）·AC-13AB=32AC2-12AB2+AB·AC.

所以AB=3AC，ABAC=ABAC=3.

評注 本题虽说运算量较大，但算是一道基础题，解法入口宽：解法1与解法2用到了平面几何中的平行线分线段成比例定理，因而减少了运算量;解法3是建立平面直角坐标系，突出了平面向量的数形结合特点;解法4运用平面向量基本定理，求出了参数λ，μ的值，从而完成求解.