开关磁阻电机直接转矩控制方法的优化

李梦茹，冬 雷,2，于坤洋，高孟祺,2

(1.北京理工大学 自动化学院，北京 100081；2.北京理工大学 唐山研究院，唐山 063000；3.中国人民解放军93126部队，北京 100086)

0 引 言

开关磁阻电机驱动系统是从20世纪80年代迅速发展起来的一种新型调速电机驱动系统，由开关磁阻电机(以下简称SRM)、功率变换器、控制器和检测器4个部分组成。它的结构十分简单坚固，而且调速范围和调速性能都具有比较优秀的表现，系统的可靠性高，是各国研究和开发的热点之一[1]。转矩控制性能的好坏直接决定了电机驱动系统的性能。相电流的非线性变化以及由脉冲转矩叠加而成的合成转矩不是恒定值，是SRM转矩脉动的根源，尤其在电机低速运行时，转矩脉动更加明显[2]。

文献[3]首次介绍了在传统SRM中应用直接转矩控制(以下简称DTC)的方法，而其他学者则多是以此研究为基础进行深入的。文献[4]采用2个PI调节器来代替常规DTC中的滞环控制器，使其具有更好的转矩脉动和速度响应性能。固定的磁链参考值不能同时适用于SRM的低速和高速运行，使用较大的磁链参考值虽然可以增大转矩出力，但是为达到给定磁链值会导致绕组中电流过大，转矩脉动变大并且降低电机运行效率。为了解决固定不变的磁链参考值带来的转矩脉动问题，文献[5]提出可以根据转速控制参考磁链值，优化后的参考磁链不再受电机运行速度的限制，有效地降低了转矩脉动。文献[6]分析了磁链参考值对电机运行性能的影响，结果表明，在运行过程中恒定的磁链会使电机的转矩电流比减小，进而提出了一种优化的转矩电流比控制方法。文献[7-9]进一步提出，在DTC中可以不使用磁链闭环，并在实验中验证了其效果更优。

本文以减小转速稳定后的转矩脉动和增大转矩电流比为优化目标，分析传统DTC方法转矩脉动大的原因，提出了相应的优化算法，即一种适用于四相SRM的不产生负转矩的电压矢量和开关表的优化方法。

1 SRM DTC方法

1.1 传统DTC

传统的DTC方法是通过估算SRM当前时刻的磁链和转矩，计算实际磁链与给定磁链的差值、实际转矩与由转速环计算得到的参考转矩的差值，分别经过磁链滞环比较器与转矩滞环比较器，判断下一时刻磁链和转矩应该增大或者减小，将判断得到的控制信号输入内置开关表，结合当前合成磁链矢量的方向选择合适的电压矢量，在该电压矢量的作用下将实际转矩与参考转矩的差值、实际磁链与给定磁链的差值限制在滞环比较器的滞环内，维持磁链和转矩的恒定，达到对转矩和转速的控制目标。若不计定子绕组的电阻，则一相电压平衡方程可以近似：

(1)

式中：Ψ表示相磁链；U表示相电压。

由式(1)可知，绕组磁链的变化是由对绕组施加的电压矢量决定的[10]。若施加的电压矢量与定子磁链的夹角|φ|<90°，那么定子磁链的幅值将增加；如果|φ|=90°，那么定子磁链的幅值将将保持不变；如果|φ|>90°，则定子磁链幅值将减小[11]。SRM绕组中的电流只有一个方向，定义为正向，那么转矩值仅取决于磁链矢量随转子位置角的变化。若施加的电压矢量超前磁链矢量，电磁转矩增大；若施加的电压矢量滞后磁链矢量，电磁转矩减小。

根据磁链值与转矩值，结合扇区，选择合适的电压矢量。

采用经典的四相不对称半桥型功率变换器，该变换器由直流电压供电，包括4路相互独立的相电路，可以对每一相单独控制。其中每相电路仅包括该相绕组、2个开关管和2个续流二极管，结构简单。通过分别控制2个开关管的导通与关断，可以组成3种不同的状态[12]。不对称半桥电路的电路模型如图1所示。以A相绕组为例，当Q1、Q2导通，绕组两端电压为母线电压，定义此时电路状态为“1”，电流回路如图1(a)所示；当Q1关断、Q2导通，绕组中的电流经过D2、Q2续流，定义此时电路状态为“0”，电流回路如图1(b)所示；当Q1、Q2均关断，定义此时电路状态为“-1”，电流回路如图1(c)所示，若此时绕组通过D1、D2续流，绕组承受负压电流将迅速下降，相比之下，“0”状态时回路中只有绕组电阻，因此电流会缓慢减小。

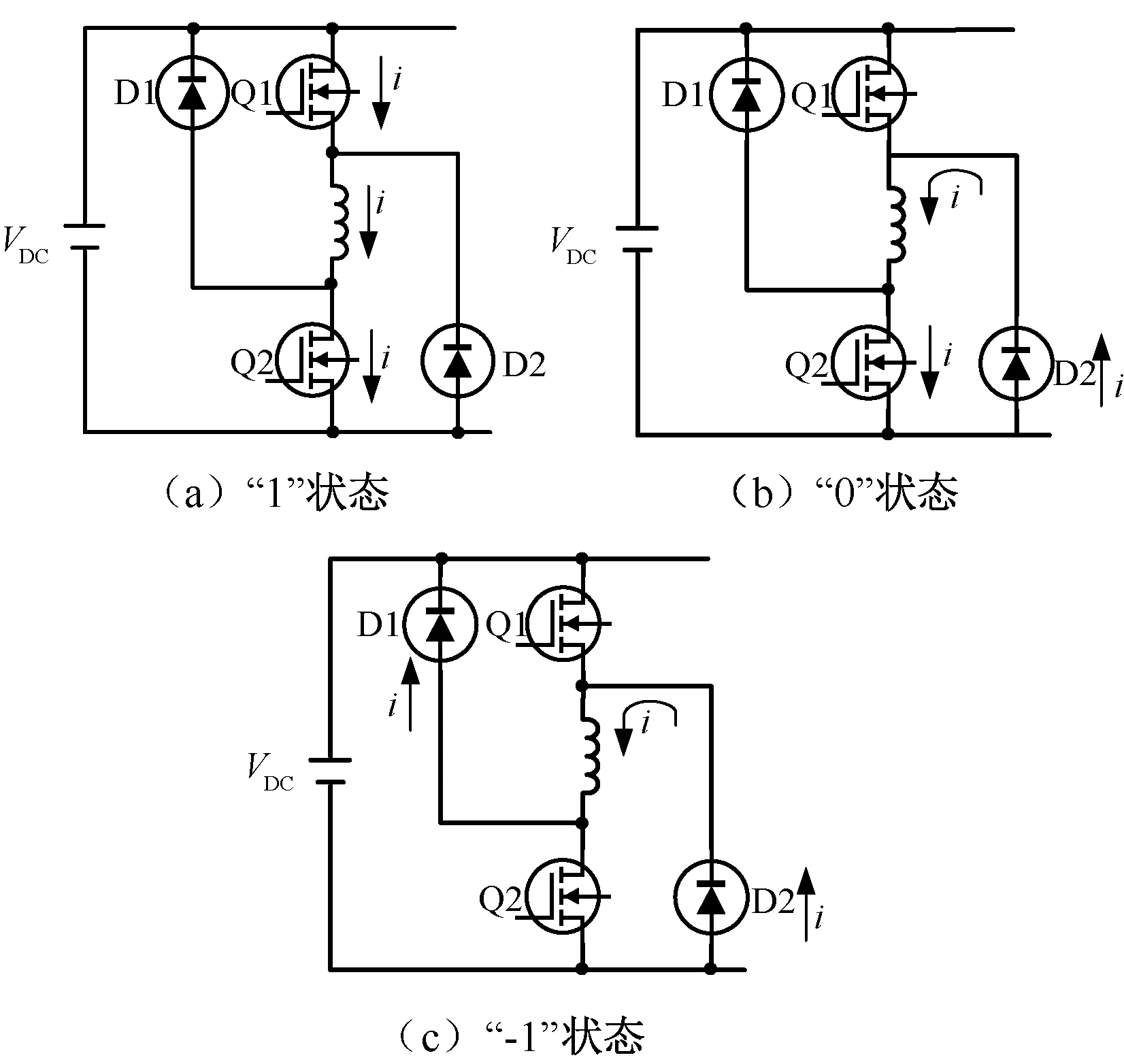
图1 功率变换电路

将四相开关管状态的组合视为1个电压矢量，8个电压矢量命名为U1,U2,…,U8，如图2所示，再以8个电压矢量为中心线将整个电空间角度划分为8个扇区，分别定义为S1～S8。磁链ψ和转矩T的增大或减小共4种组合，开关表如表1所示。

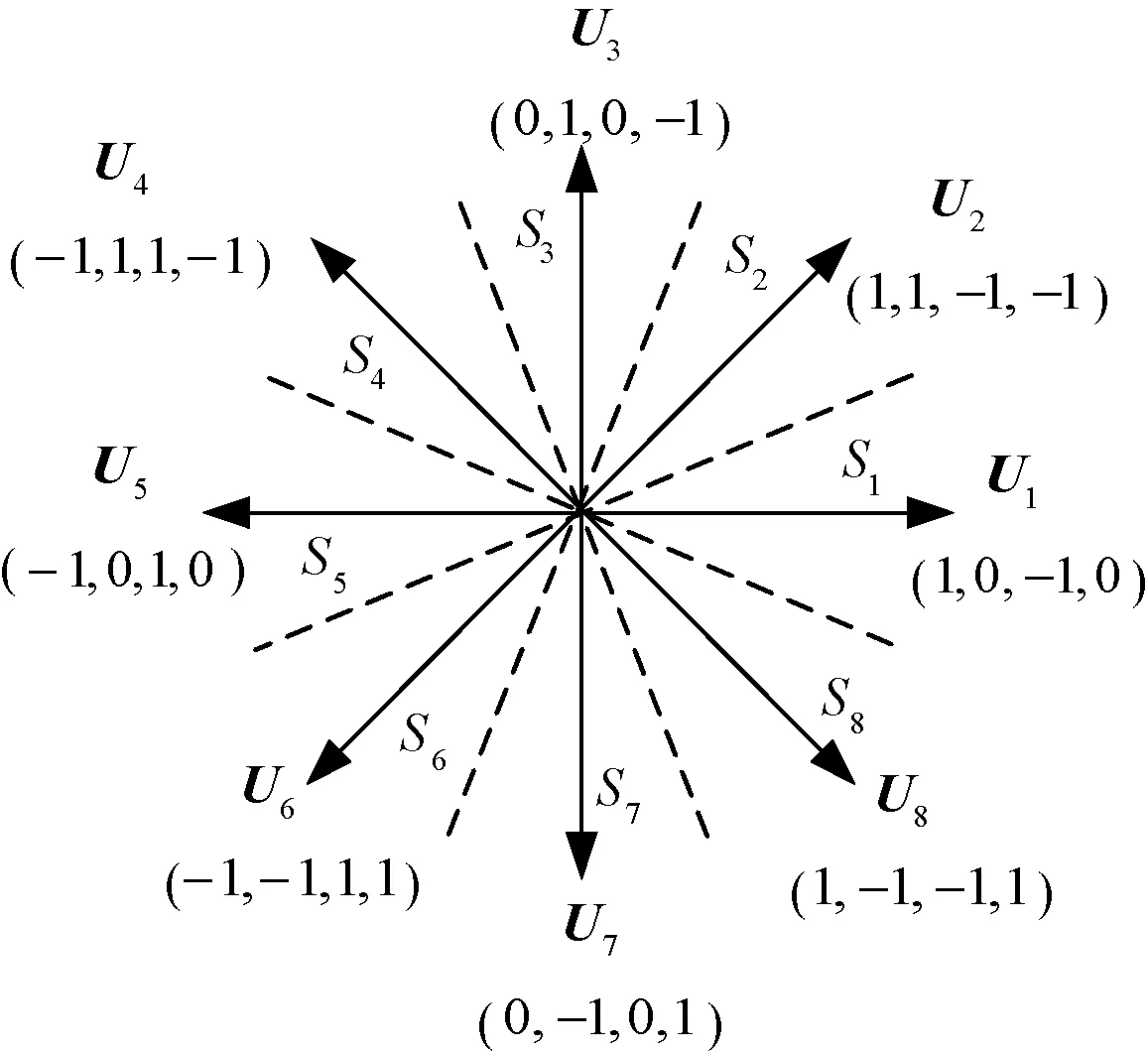
图2 8/6极SRM传统DTC电压矢量

表1 SRM传统DTC开关表

1.2 转矩脉动分析

当定转子在对齐位置处，相电感最大；当定转子在不对齐位置处，相电感最小。理想情况下，电感随转子位置角线性变化如图3所示。在电感上升区间是该相的正转矩区，电感下降区间是该相的负转矩区。SRM每相的正转矩产生区间从该相不对齐位置(0°机械角度)开始，结束于对齐位置(30°机械角度)。

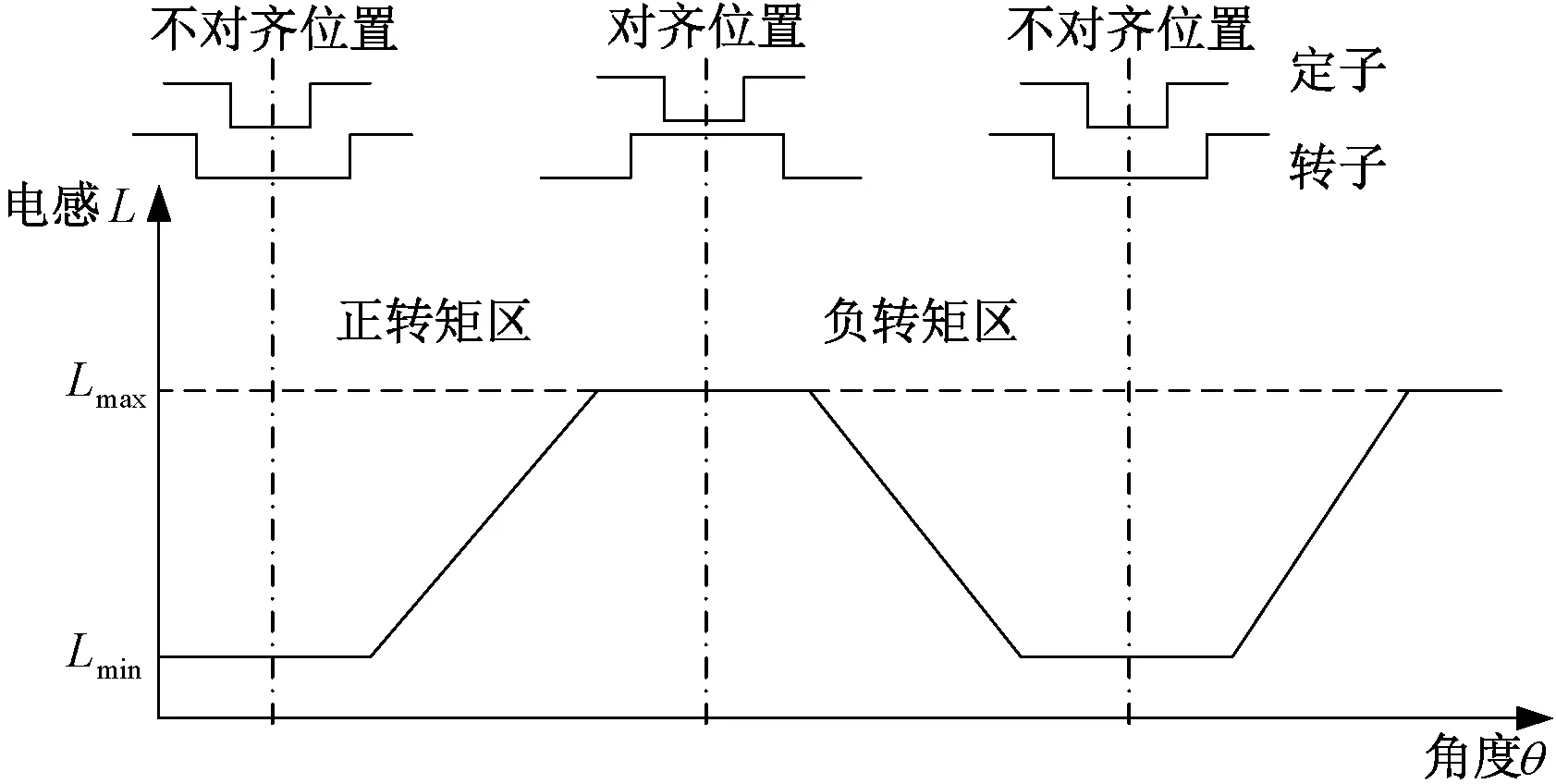
图3 SRM电感随转子位置周期性变化分布图

相电流的非线性变化以及由脉冲转矩叠加而成的合成转矩不是恒定值是SRM转矩脉动的根源。SRM之所以具有较大的转矩脉动，是由于[12]一般采用转矩-电流-角度曲线来描述SRM每相的转矩特性。当SRM处于换相阶段时，下一个导通相不能产生足以补偿因当前相关断而损失的电磁转矩，因此产生SRM的转矩降落。若要减小转矩脉动，换相位置的转矩降落越小越好。

在换相过程中，虽然当前相关断，但由于绕组电流无法突变，电流的退磁需要一定的时间，退磁过程中的拖尾电流若进入了负转矩区也将产生一定的负转矩。以扇区S1为例，若要使转矩增大，根据表1，应选择U2(1,1,-1,-1)。S1扇区为换相时刻，此时A相处于定转子对齐位置，即将进入负转矩区，所以A相为关断相，C相为导通相。此时B相主要提供转矩，C相应适当励磁辅助提供转矩，补偿由于关断相去磁导致的正转矩缺失。若对A相主电路施加“1”状态，则A相产生负转矩；若对C相主电路施加“-1”状态，则C相保持关断，无法在换相时刻提供转矩。如此一来，不仅总转矩的增大过程缓慢，而且在换相时刻会引起较大的转矩脉动。显然，在S1扇区，U2并不是最优转矩增大电压矢量。

2 电压矢量重构

SRM具有独特的电机结构和磁链特性，其转矩生成原理与交流电机不同，因而传统DTC方法维持磁链近似圆形的原则对SRM并不适用。取消磁链滞环控制后，采用稳定且较为缓慢变化的转子位置角判断扇区，具有更高的准确性。

8/6极SRM的机械角度和电角度存在以下关系：

θele=θrNr

(2)

式中：θele表示电角度；θr表示转子机械角度；Nr表示转子极数。

四相8/6极SRM每转有24个步距，步进角为15°。四相依次通电后，转子将转过60°，即360°电角度，视为一个周期。则在一个周期内各相的对齐位置与不对齐位置的角度关系如图4所示，并以此重新划分区间S1～S8。

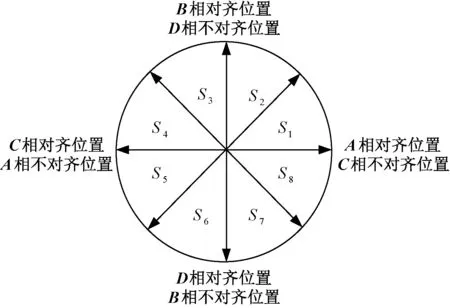
图4 优化的DTC方法的区间划分

2.1 增转矩电压矢量重构

以S1扇区为例，若A相励磁关断不及时，A相电流进入S1扇区(即A相负转矩区)，A相将产生负转矩，任何负转矩的产生都会导致转矩电流比降低。实际上，仅调整工作相就能达到转矩的调节。在换相区之间，为了防止产生负转矩，关断相要及时去磁，而导通相要适当励磁，以弥补因关断相的去磁所造成的正转矩缺失。

新的电压矢量组构建原则是在绕组即将进入电感下降区间前，提前关断该相开关管，保证相电流有足够的时间下降为0；并且对已经位于电感下降区间的绕组，严禁对其励磁。以A相绕组为例，图4中S1～S4扇区为A相电感下降区，此时若对A相绕组励磁则会产生负转矩，所以在整个S1～S4扇区A相电路状态都应该为“-1”；S5～S8扇区为A相电感上升区，此时为保证A相转矩出力，应对A相绕组励磁，S5～S8扇区A相电路状态都为“1”。但是为了避免A相电流进入S1扇区，在S8扇区内应使A相电流迅速下降，所以更改S8扇区内A相电路状态为“-1”。其余三相绕组位于各个扇区内功率变换电路状态设计与A相类似，其他扇区的增转矩电压矢量选择如图5和表2所示。

图5 增转矩电压矢量组

表2 增转矩电压矢量选择表

2.2 减转矩电压矢量重构

在传统的DTC方法中，当实际转矩高于参考转矩，需要减小电磁转矩输出时，通过导通位于电感下降区的绕组相产生负转矩抵消超出参考转矩的部分。对于图5中优化的电压矢量，当然也可以采用这种方法。例如，转子位于S1扇区时，若需转矩增大，可以选择图5中的U4；若需输出转矩减小，可以选择图5中的U8。但是对于稳定运行的SRM，可以采用减小工作相的输出转矩，使超出参考转矩的部分正转矩降落更平缓，不仅达到了温和地调节转矩的目的，而且提高了使转矩电流比。因此，表2中的电压矢量只适合增大转矩时使用，各扇区内使转矩减小的电压矢量需要重新设计。

以S1扇区为例，此时A相与D相都处于负转矩区，为了获得更高的转矩电流比，A相与D相均不能施加励磁产生电流，因此，在整个S1扇区A相与D相都应施加“-1”状态；在S1扇区内，B相主要提供输出转矩，若要减小输出转矩，可以停止对B相励磁，施加“-1”状态使电流快速下降，但是此时B相并不在换相区，电流并不需要降为0，并且B相过快的电流下降会导致较大的转矩振荡，所以在整个S1扇区对B相施加“0”状态，使B相电流缓慢下降，并且B相始终承担输出转矩。C相此时刚刚进入正转矩区，只能提供有限的正转矩，且相电感较小，若施加“-1”状态电流很快下降，后续区间将无法达到较高电流幅值提供足够的正转矩，所以在整个S1扇区对C相施加“0”状态，以实现后续对转矩的快速调节。于是，在S1扇区使转矩减小的电压矢量为(-1，0，0，-1)。其他扇区的减转矩电压矢量选择如图6和表3所示。

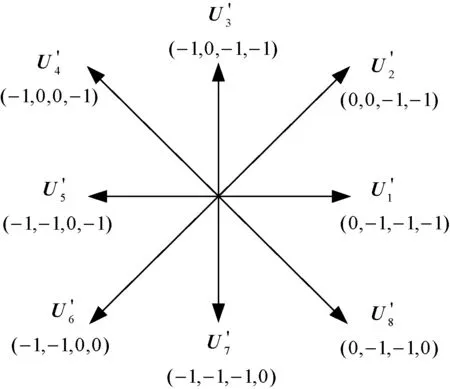
图6 减转矩电压矢量组

表3 减转矩电压矢量选择表

3 仿真及实验结果

为了检验本文优化方法的正确性，首先在MATLAB上搭建仿真模型进行算法的仿真对比，然后搭建了以8/6极SRM样机为控制对象的实验平台，并在此平台上进行实验验证。实验样机的机械结构参数如表4所示。

表4 样机机械结构参数

传统DTC方法框图如图7所示，本文优化的DTC方法框图如图8所示。可以直观地观察到优化方法更加简洁，可以实现对转矩更直接的控制，并且调试参数更少，较大程度上减小了调试难度。

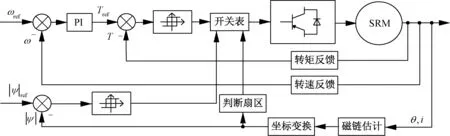
图7 传统DTC方法框图

图8 优化的DTC方法框图

3.1 仿真结果

在MATLAB/Simulink中搭建电机模型及控制算法模型。仿真参数设定如表5所示。

表5 仿真参数设置

传统DTC方法空载仿真实验总仿真时长为0.5 s，设置转速环PI控制器比例、积分系数分别为0.1和0.25，负载转矩0.5 N·m，仿真结果如图9所示。观察图9(b)，转矩很难被限制在滞环宽度内，图9(c)为稳定后的相电流与转子角度波形，实线表示电流，点划线表示转子角度，虚线表示C相角度30°分界线，双划线左侧是正转矩区，右侧是负转矩区。在负转矩区的较大电流会产生负转矩，导致转速和转矩的波动，并且会降低转矩电流比。由式(3)得稳定后的最大转矩脉动为2.115，由式(4)得稳定后的转矩电流比为0.592 4 N·m/A。图9(d)为合成磁链，在传统DTC方法下，磁链维持近似圆形。

(3)

式中：Trip表示最大转矩脉动；Tmax表示稳定后的最大输出转矩；Tmin表示稳定后的最小输出转矩；Tref表示给定参考转矩。

(4)

式中：Tavg表示稳定后的平均输出转矩；Iavg表示稳定后的相电流平均值。

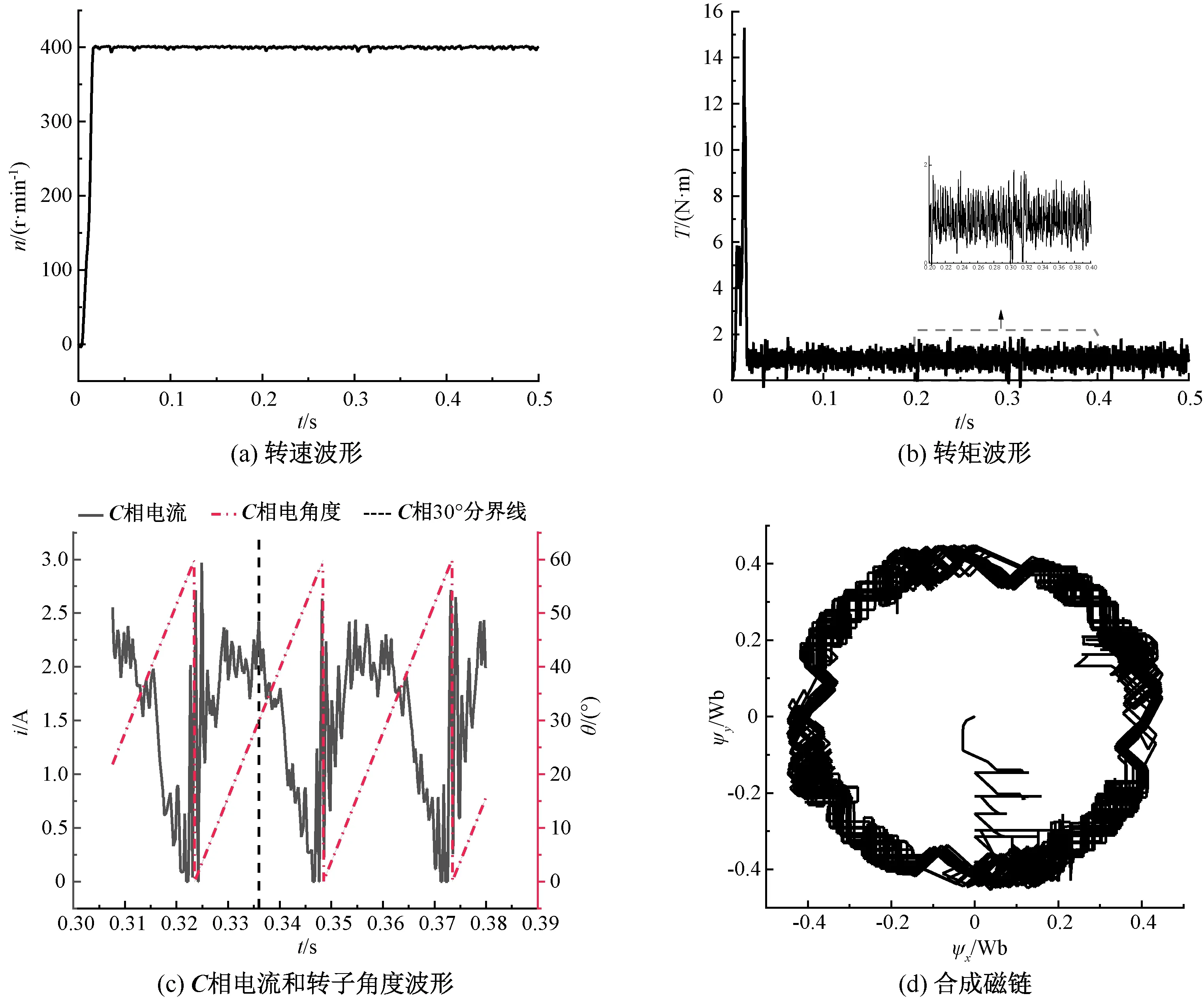
图9 传统DTC方法仿真结果

优化DTC方法的空载仿真实验的总仿真时长为0.5 s，设置转速环PI控制器比例、积分系数分别为0.1和0.25，负载转矩0.5 N·m，仿真结果如图10所示。观察图10(b)，转矩基本被限制在滞环宽度内。由图10可知，优化DTC方法的相电流更早地下降至0，在图10(c)中，实线表示电流，点划线表示转子角度，虚线左侧是正转矩区，右侧是负转矩区。电流在进入负转矩区前完全减小至零，没有负转矩产生，因此输出转矩脉动大幅减小，使得图10(a)中转速调节更加平滑。由式(3)得稳定后的最大转矩脉动0.316，由式(4)得稳定后的转矩电流比为1.293 8 N·m/A。与传统DTC方法的仿真结果相比，转矩脉动减小了85%，转矩电流比增大了118%，优化效果明显。

图10(d)为合成磁链，在优化的DTC方法下，取消了磁链滞环，磁链波形并不能维持近似圆形。这不仅减少了一个控制变量，减小了DSP负担和调试难度，而且使转速和输出转矩的性能增加。在传统DTC方法中，为了维持圆形磁链，相电流拖尾电流较大，在进入负转矩区前相电流未降至零，因此产生负转矩，导致转速和转矩的波动，并且会降低转矩电流比。

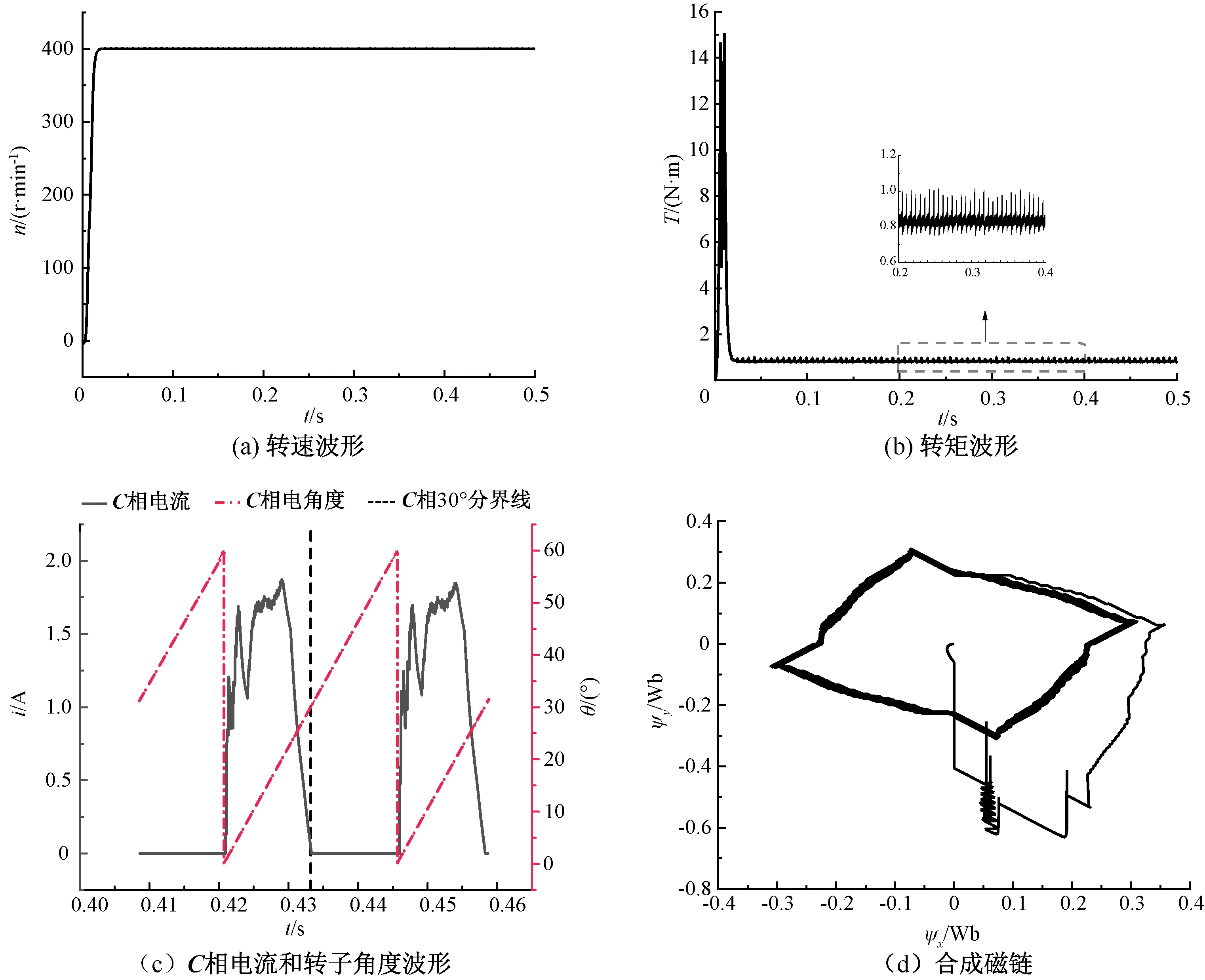
图10 优化的DTC方法仿真结果

3.2 实验结果

分别采用传统DTC方法和优化后的DTC方法驱动实验样机空载旋转，通过实验结果验证本文算法的有效性。转速和位置角使用磁编码器AS5048A测算得到，相电流由电流霍尔检测得到；通过查表法得到转矩值和磁链值。控制周期为0.5 ms，每2.5 ms记录一次实验数据，空载实验的参数设置如表5所示。

图11展示了传统DTC的实验结果。从图11(b)中可以看出，转矩波动较大，最大转矩脉动为13.83，因此转动过程中的转速波动和噪声也很大。图11(c)中，实线表示电流，点划线表示转子角度，虚线左侧是正转矩区，右侧是负转矩区。可以发现，在负转矩区仍有电流导通且持续较长时间，导致了负转矩的产生，这是传统DTC方法转矩脉动大的根本原因，转矩电流比为0.11 N·m/A。

本文在系统运行1.25 s时给予系统给定转速阶跃至600 r/min，转速波形如图11(d)所示。从图11(d)可以看出，在传统DTC方法下，虽然转速能跟踪上给定转速，但是存在较大的脉动。

图12展示了优化DTC方法的实验结果。最大转矩脉动为1.382。图12(c)中,实线表示电流，点划线表示转子角度，虚线左侧是正转矩区，右侧是负转矩区。相电流在进入负转矩区之前已经下降为0，并且在整个负转矩区不再对该相绕组励磁，C相电路状态保持为“-1”，因此没有负转矩产生，起到抑制转矩脉动、增大转矩电流比的效果，转矩电流比为0.372 N·m/A。

图12(d)展示了本文优化的DTC方法下的突加速实验转速响应曲线。可以看出，该方法不仅能快速准确跟随给定转速，并且与传统DTC方法相比，优化的DTC方法的响应过程更平稳，转速稳定后具有更小的脉动。

4 结 语

本文分析了传统DTC方法转矩脉动大的根本原因，提出了一种优化的DTC方法，并给出了适用于8/6极SRM的电压矢量和开关表，能够进一步抑制转矩脉动。对电压矢量和开关表进行优化后，电压矢量选择更加致力于转矩的调节，能够避免负转矩的产生，转矩脉动因此减小，从而提高转矩电流比。本文的优化方法也同时减小了参数调试难度，可行性更高。新方法在实验效果中使得转矩脉动比传统方法减小了90%，转矩电流比由0.11 N·m/A提高至0.372 N·m/A。实验结果证明了优化的DTC方法可以有效减小转矩脉动并且增大转矩电流比。

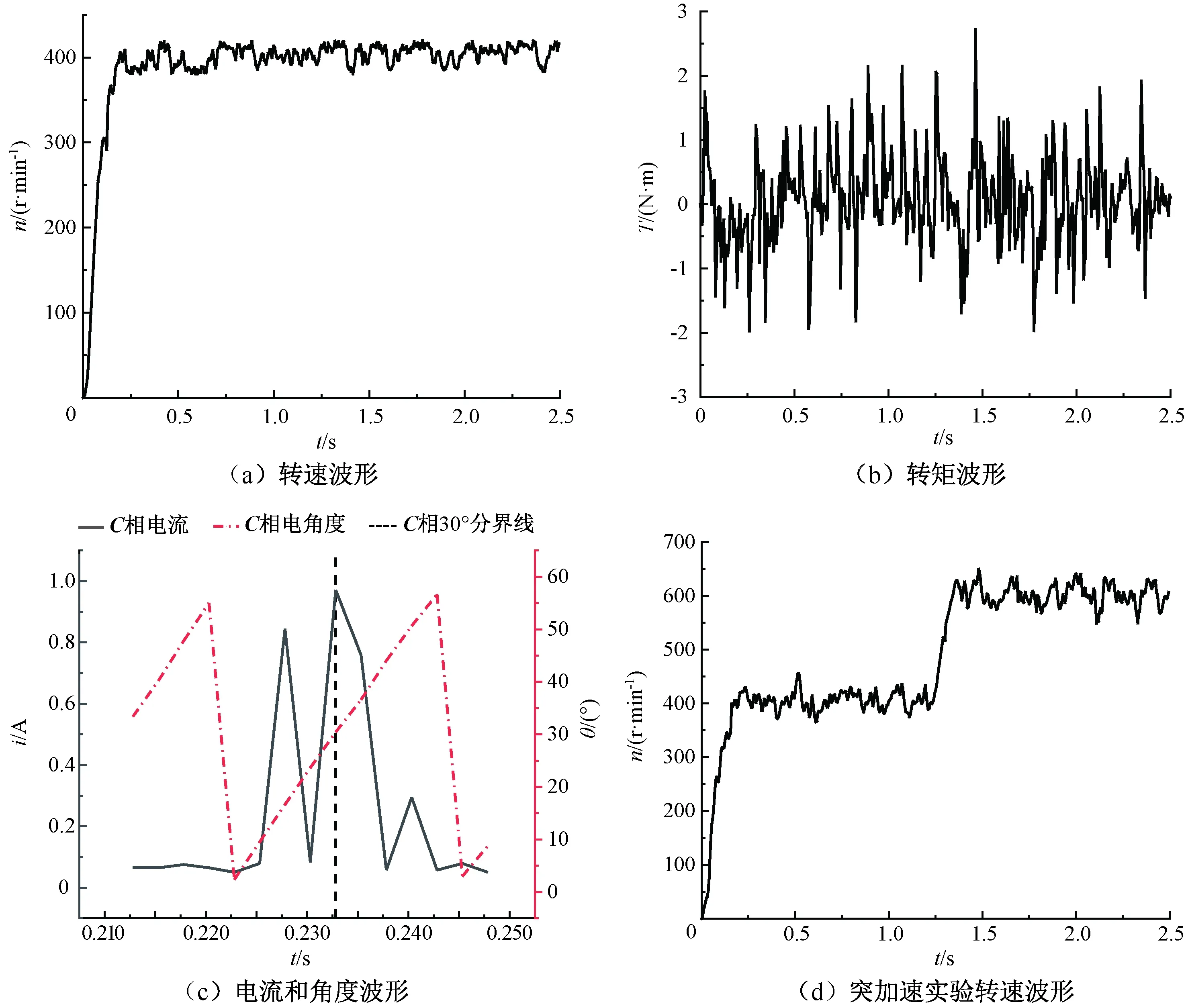
图11 传统DTC方法实验结果

图12 优化的DTC方法实验结果