自寻优最大转矩电流比矢量控制连载之三:同步磁阻电机电感扫描的虚拟信号注入法控制
2022-11-18张雨馨王云冲徐彬涵沈建新
张雨馨,王云冲,2,史 丹,徐彬涵,沈建新,3
(1.浙江大学 电气工程学院,杭州 310027;2.浙江省电机系统智能控制与变流技术重点实验室,杭州 310027;3.流体动力与机电系统国家重点实验室,杭州 310027)
0 引 言
针对同步磁阻电机(以下简称SynRM)的最大转矩电流比(以下简称MTPA)控制,学者们提出了多种虚拟信号注入法(以下简称VSIM)[1-7]。信号注入法通过注入前后的转矩值来提取判定MTPA点的信息。真实的信号注入法[8]可通过测量获取注入前后的转矩值,而VSIM不具备此测量条件。VSIM的解决方案是构建注入信号后的转矩数学模型,通过近似计算来获得注入后的转矩数据。VSIM没有真正注入信号,不会造成额外损耗,同时保留真实信号注入法计算方便、动态响应快的优点。
VSIM常用的虚拟注入信号有正弦波[1-2]和方波[3]。采用虚拟正弦波信号注入法的控制模块涉及大量信号处理环节,引入较多滤波器,算法动态性能较差,而采用虚拟方波信号注入法可以解决这些问题。同时文献[3]修正了虚拟注入控制法的方程,引入了与d轴电感参数有关的补偿项,提高了算法的稳态精度。该算法将此补偿项中的d轴电感参数视为常数,取空载下的d轴电感为近似。然而SynRM参数是非线性变化的,当电机进入饱和区工作时算法的稳态控制精度会下降。
考虑到SynRM参数非线性变化的特性,本文采用引入补偿项的转矩模型,将其中d轴电感参数作为优化搜索变量,获得考虑电机参数非线性的精准转矩模型,在此模型上进行虚拟双极性方波信号注入MTPA寻优,可以有效补偿电机参数非线性变化带来的误差,取得较好的MTPA控制效果。该方法可以避免如传统搜索法直接对电流矢量角进行高时间成本的搜索,在虚拟信号注入法的基础上对电感参数进行扫描,间接实现极值搜索,具有更高的控制精度和动态特性。
1 SynRM模型
三相SynRM在d-q参考坐标系下的模型可以表述:
(1)
(2)
(3)
(4)
iq=Iscosβ
(5)
id=-Issinβ
(6)
式中:vd,vq分别为d,q轴电压;id,iq分别为d,q轴定子电流;Ld,Lq分别为d,q轴电感;R为定子电阻;Te,TL分别为电磁转矩和负载转矩;ωm为转子的机械角速度;p为电机极对数;Bm为摩擦系数;J为转动惯量;Is为电流矢量的幅值;β为电流矢量超前q轴的相位角。
SynRM转子没有永磁体,从式(3)可以看出,其转矩主要为d,q轴电感差导致的磁阻转矩。运行过程中电机的磁路会随着定子电流的变化发生非线性的饱和,同时受到交叉耦合的影响,d,q轴电感随着d,q轴电流的变化而变化。因此SynRM参数具有显著的非线性变化特性,在控制过程中不可忽略。
针对SynRM MTPA控制,传统的45°电流相位角公式法在控制过程中将电机电感参数视为常数,忽略参数的非线性变化,难以实现准确的MTPA控制。电机参数的非线性变化难以用模型准确拟合,故LUT和在线参数辨识法需要进行复杂的工作且难以实现精准的控制。为考虑SynRM参数非线性特性,同时不依赖参数,学者们提出搜索法来实现精准的MTPA控制。
2 基于电流相位角搜索的MTPA控制原理
2.1 电流相位角极值搜索原理
搜索法将电机系统看作一个黑箱,不考虑具体的电机模型及参数,其核心是以电流相位角为优化变量,以最小化电流幅值为优化目标,通过不断检索寻优找到使电流幅值最小化的MTPA点。具体可通过向电流相位角施加一定扰动信号,根据反馈回来的电流幅值的变化情况,在线搜索对应于电流最小时的MTPA点。不同的扰动信号、搜索方式对应不同的控制精度,下面以正弦式扰动为例描述电流相位角极值搜索原理。电流相位角扰动调制方式的数学描述:
(7)
式中:β为电机稳态运行时的电流相位角;k1为相位角变化方向,取+1或者-1;k2为相位角调制的幅度;ti为控制周期中的采样时间。
电流相位角的扰动会引起电流幅值的变化ΔIs,常用的判断方式为阈值三段式,需提前预设一个阈值ΔI阈。
1) ΔIs小于-ΔI阈,说明当前工作点下相位角的调整可以有效降低电流大小,维持相位角变化方向k1不变,同时更新相位角:
βbase,new=βbase,old+k1k2
(8)
2) ΔIs大于ΔI阈,说明当前工作点下相位角的调整反而导致电机电流增大,需要改变相位角变化方向,对k1取反,同时如式(8)更新相位角。
3) ΔIs绝对值小于ΔI阈,说明当前工作点下相位角的变动对电流基本没有优化效果,可认为当前的工作点已处于最佳位置,只需维持此相位角不变即可。
以上三种情形电流相位角β的变化如图1所示。

图1 相位角极值搜索法的阈值三段式控制
图1中的正弦波动表示搜索过程中对电流相位角的扰动,根据阈值三段式的判断,对相位角进行相应的调整,可以使得电机最终稳定工作在最优MTPA点。
2.2 基于极值搜索原理的VSIM
极值搜索法直接将电流相位角作为搜索变量进行工作点寻优,以相位角施加扰动后电流幅值的变化为控制依据,不依赖参数便可实现最优MTPA控制,然而极值搜索法动态性能较差。基于极值搜索法的原理,学者们提出信号注入法,改善了算法的动态性能。信号注入法向系统中注入小信号来提取判断电机是否工作在MTPA的信息。真实注入信号会引入额外损耗,造成转矩波动等,VSIM注入虚拟的信号,克服了真实信号注入法的缺点。虚拟单极性方波注入法便属于VSIM的一种。
虚拟单极性方波注入法采用占空比为50%的方波作为虚拟信号:
(9)
式中:N=1,2,3…;δ和Ts分别表示方波信号的幅值和周期。
对注入虚拟方波信号后的转矩进行泰勒展开及忽略二阶及以上导数项,可得:
(10)

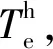
(11)
式中:Ld的值采用空载下的Ld值做近似。
根据前述对SynRM模型的分析,电机的电感参数是非线性变化的,将其视为常数则将降低MTPA寻优的准确性。实际上每一个电感值Ld均对应了一个虚拟信号注入法的参考转矩模型,结合极值搜索法的原理,可将Ld看成类似电流相位角的一种决定控制系统性能的参数,通过检索Ld以决定最佳参考转矩数学模型。最佳工作相位角再经由最佳参考转矩模型进行虚拟信号注入法寻迹得到。
本文基于虚拟双极性信号注入法系统,通过扫描搜索最优的电感参数Ld,并以式(11)重建转矩模型,从而间接实现极值搜索,这种方式结合了传统VSIM动态响应快速的优点,可避免直接对电流相位角进行搜索造成的高时间成本。
3 电感参数扫描MTPA控制算法
3.1 电感参数扫描MTPA基本原理
考虑到MTPA的控制目标为最小化给定转矩下所需的电流,电机的实际电流值可以通过电流传感器直接观测,因此基于VSIM的电感参数扫描法以电流矢量幅值作为监控目标,通过记录每一轮电感值扫描变化后的电流幅值,以决定适配当前工况的最佳电感值,并以此电感值作为当下VSIM中重建转矩模型里的电感值Ld。
具体控制思路:首先,基于当前电感值的转矩模型,采用VSIM控制电机,记录电机的稳态电流值。然后对电感施加小偏移量,VSIM根据更新后的电感值再次寻优相位角。在算法稳定之后,记录下新稳态下的电流值。通过比较两次稳态的电流值可以判断电感值修正产生的是正向作用还是反向作用,从而决定下一次电感值的修正方向。其工作原理如图2所示,图2中θ为由于电机的机电常数而产生的时延值。

图2 电感参数扫描法原理图
图2中,电感参数扫描可以分为两种情况处理:
1) 如图2(a)所示,电机在新稳态下的电流值比之前值更大,需改变电感扫描的方向,并舍弃此时的电感值,沿用之前的电感作为电感基值;
2) 如图2(b)所示,电感值偏移后,电机在新稳态下的电流值比之前值更小,说明此时更新的电感值更加逼近最佳电感。维持电感扫描的方向,且将偏移后的电感值更新为新的电感基值。
图3展示了电感参数扫描法控制下电机工作点在转矩曲线上的变化过程。实线为考虑参数非线性变化特性的SynRM的真实转矩曲线,虚线为采用不同电感值对应的参考转矩模型。电感扫描法迭代更新电感值来修正参考转矩模型,此过程以实线箭头指示在图3中。可以看到,电机经过不断迭代,最终能够稳定工作在MTPA点,实现良好的控制效果。

图3 电感参数扫描法控制过程
3.2 双向增量电感探测机制
合理搜索步幅能较大提高搜索法的控制效率。电流相位角极值搜索法采用的传统阈值三段式法的步长是固定的,无法依据与最佳点间的距离和电机参数范围进行灵活调整,且阈值设计的精准度会影响判断工况变化的灵敏度。本文设计双向增量电感探测机制,可以同时确定电感值变化的方向和步长,根据控制效果和工况进行灵活调节。
双向电感探测机制设计如下:
1) 基于当前电感值的参考转矩模型进行VSIM控制,当电机运行到稳态时记录当前的电流值Io;
2) 令Ld正向偏移ΔL,基于新的电感值运行VSIM直至稳定,记录此时的电流值Ipos;
3) 令Ld负向偏移ΔL,同样记录系统稳定后电流值Ineg;
4) 通过比较Ipos和Ineg来修正Ld,更新公式:
Lbase,new=Lbase,old-k(Ipos-Ineg)
(12)
式中:k为电感更新系数。
5) 重复上述步骤至电流稳定趋向定值。
ΔL被称为探测电感,其值相对而言比较小,这样设计的目的在于令系统稳定时不会引起大的模型振荡而导致电流中出现较大的纹波。双向增量电感探测机制的逻辑原理如图4所示。
图4 双向增量电感探测机制原理
图4(b)中,当正向探测结果和反向探测结果横跨在极值点的两端时,当前的电感能稳定落在最佳电感值处,实现最优MTPA控制。此外,电感的更新步幅与正向探测和反向探测得到的电流差值线性相关,故算法在不同电机模型和工况变动中均能自适应调整电感参数扫描步幅直至稳定,实现高性能控制。
4 仿真分析
首先对电感参数扫描法进行理论仿真。在Simulink中搭建的SynRM模型的电感参数是非线性变化的,与被控制电机的有限元仿真结果一致,在控制过程中通过查表获得。电机参数如表1所示。

表1 SynRM参数
4.1 稳态性能研究
将仿真得到的电感参数扫描法与传统的虚拟单极性方波信号注入法控制下的电机稳态电流幅值的结果进行对比,如表2所示。仿真中给定负载转矩分别为2 N·m、4 N·m、6 N·m、8 N·m,给定转速为600 r/min。

表2 600 r/min下SynRM稳态电流值仿真结果
从表2中可以看出,考虑了SynRM非线性特性的电感参数扫描法具有更高的稳态精度,较大地减小了电机稳态电流幅值,能有效降低电机损耗,提升电机效率。
4.2 暂态性能研究
在给定转速为600 r/min,给定负载转矩在t=2.5 s时刻由2 N·m突变至6 N·m工况下,观察电机在电感参数扫描法控制下电流幅值、电流矢量相位角的变化,并将结果与虚拟方波信号注入法的暂态响应结果作比对。
图5展示了两种MTPA方法控制下电机电流幅值Is的暂态波形。可以看到,由于电感参数扫描法考虑了电机参数非线性特性,对电感参数进行极值搜索,搜寻最优电感值,相比于虚拟单极性方波注入法有了较大的提升,其控制下的电机电流幅值比虚拟单极性方波注入法小,并且随着转矩的增大,算法的优化效果更显著。
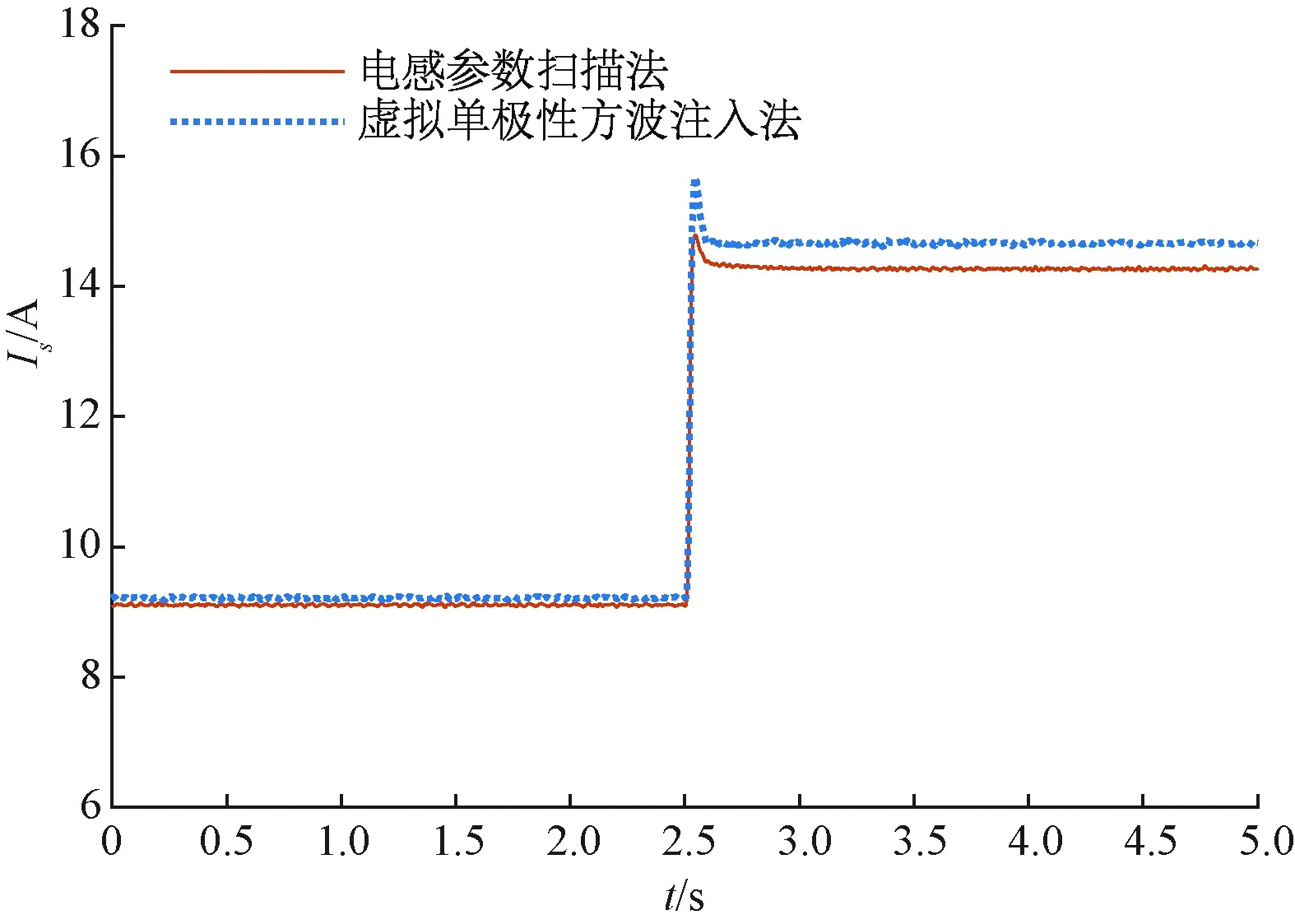
图5 600 r/min变负载下的电流幅值波形
图6展示在两种MTPA控制方法下电机电流矢量相位角β的暂态响应波形。可以看出,负载突变后,本算法的电流相位角经一段时间后基本进入稳定,但由于采用双向增量探测机制,电机的电流矢量相位角会小幅振荡。结合图5可以看出,相位角的小幅振荡并不影响电流幅值的稳定性,依然可以实现稳定且精准的MTPA控制。

图6 600 r/min变负载下的电流相位角波形
此外,图7展示了本方法控制下电机d,q轴电流id,iq的暂态响应过程。事实上,从图5的电流幅值Is和图6的电流相位角β可以直接推导出id与iq(见式(5)和式(6))。虽然β有小幅变化,但经三角函数运算后,id与iq基本稳定。从图7中可以看出,在负载突变的工况下,id与iq能实现快速响应,具有良好的动态性能。
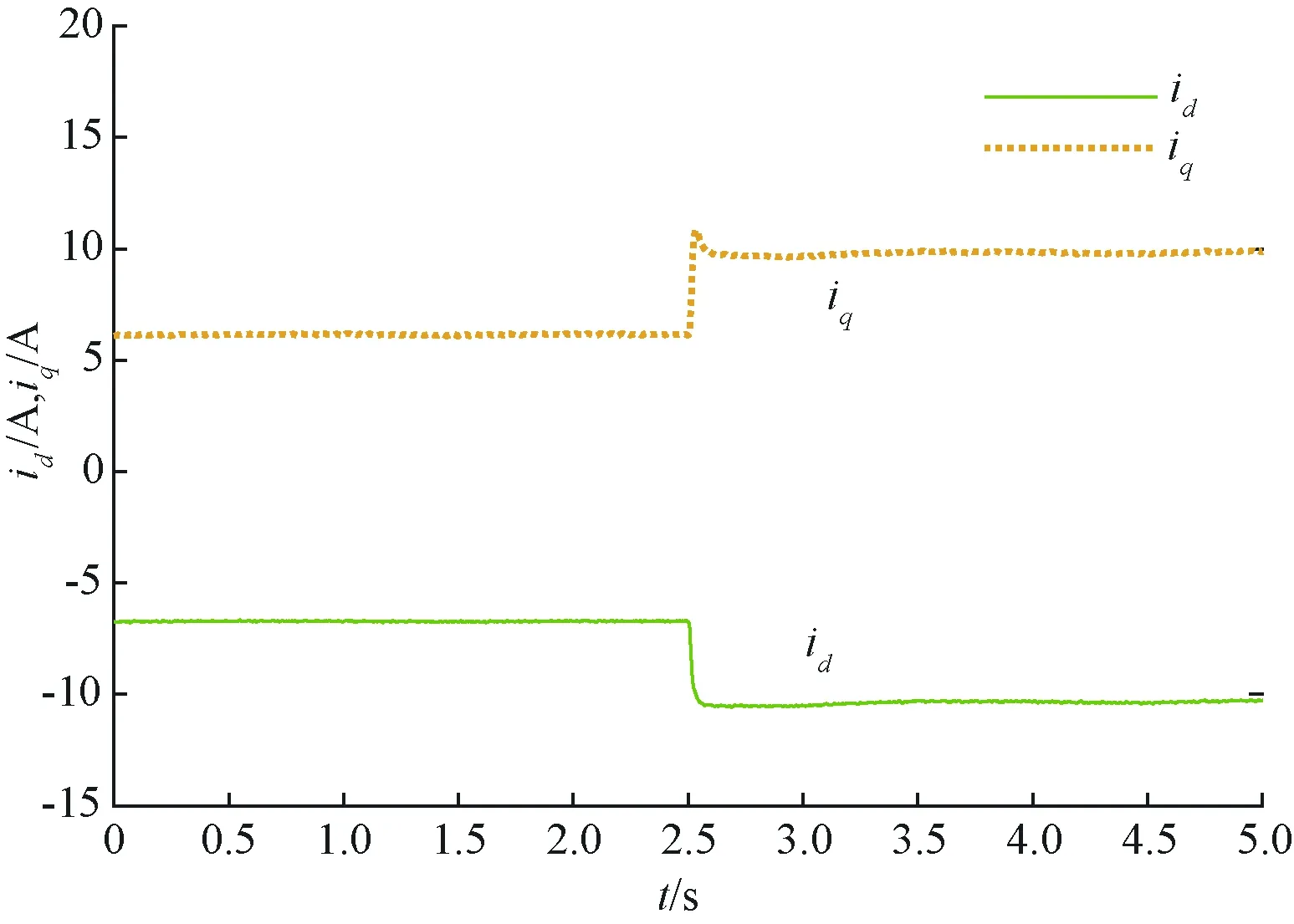
图7 600 r/min变负载下的id,iq波形
5 实验验证
本文搭建了SynRM实验台架,对电感参数扫描法的控制性能进行实验验证。台架主要由被控SynRM和作为对拖负载的PMSM组成,两台电机经扭矩传感器连接。PMSM输出的三相电流经整流桥连至电子负载,通过电子负载调整负载的大小。SynRM由Myway系统控制,Myway系统主要由SiC逆变器和PE-Expert4控制器组成,PE-Expert4搭载了处理数字信号的DSP (TMS320C6657)高性能控制板。逆变器直流侧施加300 V母线电压,被控SynRM的相关参数如表1所示。
5.1 稳态性能研究
在给定电机转速600 r/min,负载转矩分别为2 N·m、4 N·m、6 N·m、8 N·m四种工况下,观测参数扫描法控制下SynRM的稳态电流幅值,并且与传统虚拟单极性方波注入法控制下的结果作比较,如表3所示。
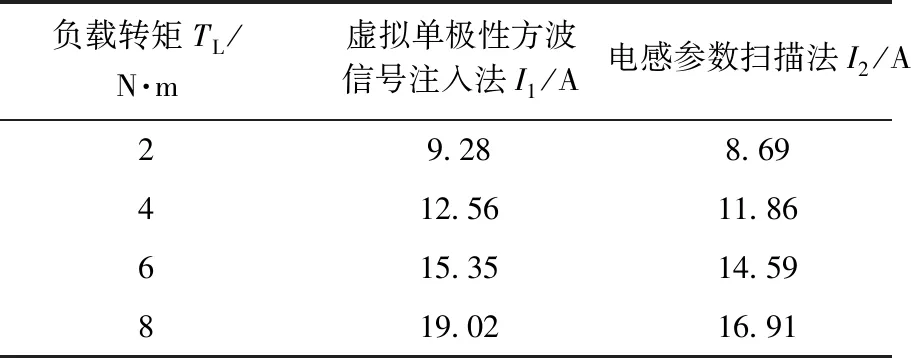
表3 600 r/min下SynRM稳态电流值实验结果
从表3中可以看出,由于电感参数扫描法考虑了参数的非线性变化,以电感为优化变量进行极值搜索,弥补了将电机电感参数视为常数的传统VSIM带来的误差,实现精准的MTPA控制,在同样的工况下较大程度地减小了电机的电流幅值,降低了损耗,提高了电机效率。

图8 SynRM三相电流给定量波形
实验中,当电机稳定运行在600 r/min、8 N·m负载下时,观测三相电流给定量,如图8所示。可以看到电机三相波形是光滑的正弦波,这是因为:电感参数扫描法基于VSIM对电感参数进行极值搜索,不会真正注入电流矢量相位角偏移信号,不会引入额外的损耗和谐波,克服了真实信号注入法的缺陷;虽然寻优后的电流矢量相位角β有小量振荡(见图6),但是d、q轴电流仍然是比较稳定的(见图7)。β的小幅振荡对电流波形质量没有明显影响。
5.2 暂态性能研究
电机给定转速为600 r/min,观察当负载转矩在t=2.5 s时刻从2 N·m突变至6 N·m时电机的电流幅值与电流矢量相位角的暂态波形图。
图9展示了采用电感参数扫描法和虚拟单极性方波信号注入法控制下电机电流幅值Is的暂态响应波形。可以看到,相比于虚拟单极性方波信号注入法,本算法控制下的电机电流幅值大幅减小,并且在重载工况下算法的改善效果更明显。在负载突变后,电流幅值波形能快速响应,具有良好的动态响应特性。
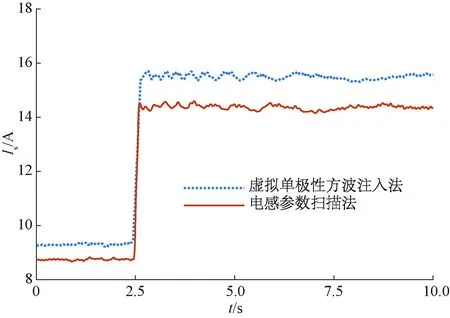
图9 600 r/min变负载下的电流幅值波形
在负载突变后的2.5 s内,由于工况突变使得转矩模型中扫描电感变化剧烈,导致这段时间内的电流幅值存在波动。但随着电机运行状态进入稳定,电感参数趋于稳定,此时电流幅值波形呈现较好的稳定性,也印证了图8中电机稳态三相对称正弦波电流波形。
图10展示了采用电感参数扫描法和虚拟单极性方波信号注入法两种MTPA控制方法下电机电流矢量相位角β的暂态响应波形。可以看到,由于本算法基于双向增量探测机制对电流矢量相位角进行极值搜索,电机的电流矢量相位角存在小幅振荡,但这并不影响图9中电流幅值的平稳性,算法依然能实现精准稳定的MTPA控制。
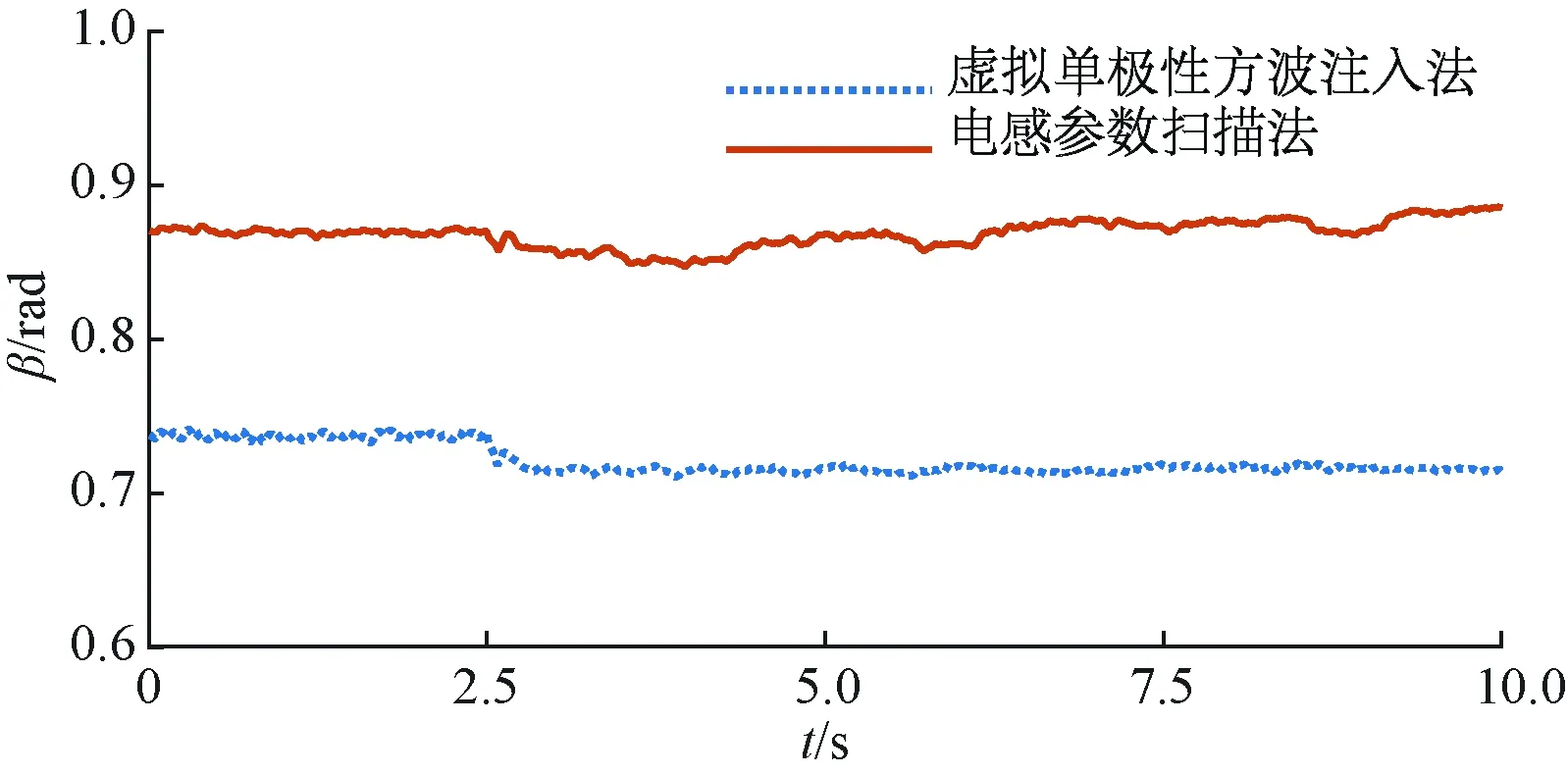
图10 600 r/min变负载下的电流相位角波形
仿真和硬件实验的结果保持了较好的一致性,结合它们的结果可以看出,相比于虚拟方波信号注入法,电感参数扫描法能够实现精准的MTPA控制,具有较高的稳态精度。尽管采用双向增量电感探测极值,优化了搜索法动态响应慢的缺点,但对电感参数的检索依然需要花费一定时间并且存在小幅振荡。相比虚拟方波信号注入法,电感参数扫描法的动态响应特性较差,其牺牲了部分动态响应性能来提高MTPA的稳态控制精度,因此不适用于工况变化频繁的场合。
6 结 语
本文在虚拟双极性信号注入法的基础上提出了电感参数扫描MTPA控制算法。考虑到SynRM电机参数非线性变化显著,本文通过扫描搜索最优的d轴电感参数变量重建转矩模型,间接实现极值搜索,该方法同时结合了极值搜索法不依赖参数、计算简便和VSIM响应快速的优点,能够实现更精准的MTPA控制。针对搜索方向和步长的设计,本文提出了双向增量电感探测机制,可以自适应调整电感参数值增量的方向和步长,提高搜索的效率和稳定性。最后通过仿真和实验验证了电感参数扫描法的MTPA稳态寻优精度优于传统的虚拟方波信号注入法,并且具有较好的动态响应特性。
该方法的缺点是,电感参数遍历扫描的执行比较繁琐,所花费的寻优时间较长,并且在稳态MTPA控制时电流相位角仍有小幅振荡,当然,该振荡对系统稳定性的影响很小。为了克服此缺点,可以采用其他方法获得最优的电感参数,如同构电感法,将在后续论文中介绍。
