基于定子磁链角度计算的PMLSM直接推力控制*
2022-03-23张宏伟崔磊磊
蒋 頔, 张宏伟, 崔磊磊
(河南理工大学 电气工程与自动化学院,河南 焦作 454000)
0 引 言
永磁直线同步电机(permanent magnet linear synchronous motor,PMLSM)相比传统电励磁直线电机有功率因数高、结构简单等优点,在轨道交通、武器发射等行业领域得到广泛的应用[1]。直接推力控制(direct thrust force control,DTFC)是继矢量控制技术之后的高性能的交流变频调速控制[2],然而,DTFC存在磁链和推力波动大、PI速度控制器鲁棒性差等问题,需要进行改进。针对DTFC存在的问题,有大致三类解决办法[3]:1)改进空间电压矢量开关表,得到恒定的开关频率[4~7];2)使用无传感器算法对直接推力控制进行改进[8~10];3)对滞环控制器和PI控制器进行改进[11~13]。文献[4]对磁链、推力和速度的回路进行了设计,将差值作为PI控制器输入。文献[5]通过电压“预测”的方法,对电机进行控制。文献[6]引入磁链“预测”的方法,减小磁链和推力的波动;文献[7]提出了基于12扇区和13电压空间矢量的方法,减小了推力和磁链的波动。文献[8]采用模糊参考自适应控制方法,控制性能也有一定提高。文献[9]结合了滑模和自适应的控制方法,其具有良好的动静态性能。文献[10]运用两个卡尔曼滤波器进行串行通信对PMLSM进行控制。文献[11~13]将速度与推力控制器换为滑模控制器,改善了控制性能。
传统DTFC的滞环控制器与电压矢量开关表之间的误差导致推力和磁链波动大。针对以上问题,本文提出了一种基于定子磁链角度计算的PMLSM直接推力控制。通过计算定子磁链矢量角度的变化来对电机的推力进行控制,将推力和磁链滞环控制器用PI推力控制器取代,减小了磁链和推力的波动。在此基础上,用积分滑模速度控制器来代替PI速度控制器,提高系统鲁棒性,且针对滑模控制器的抖动,用Sigmoid函数来代替开关函数。通过仿真实验验证了本文所提出的方法的有效性。
1 基于定子磁链角度计算的DTFC原理分析
PMLSM的电磁推力方程为
(1)
式中τ为极距;Ls为定子电感;ψs为定子磁链;ψf为动子磁链;δ为负载角。ΔT周期内,PMLSM磁链矢量变化如图1所示。
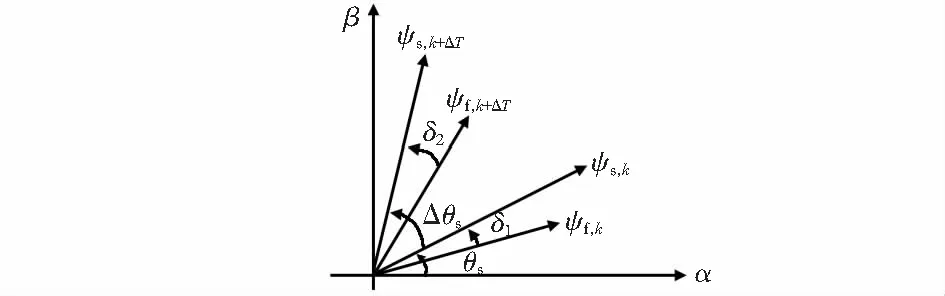
图1 PMLSM磁链矢量变化
由式(1)得出推力Fe与负载角δ有关。由图1得出
Δθs=Δδ+ωeΔT
(2)
式中 Δθ为定子磁链的角度变化量,Δδ为负载角变化量,ΔT为周期。若定子磁链矢量的模值保持不变,定子磁链角度发生改变后,则定子磁链矢量为
(3)
定子磁链的角度发生变化,得定子磁链矢量的变化量为
(4)
通过调整定子磁链控制电压矢量
(5)
由式(5)可得定子电压矢量在α-β轴投影的变化
(6)

PMLSM推力的改变量可视为定子磁链角度的变化量。同时,定子磁链的变化通过定子磁链矢量角度变化来体现,由电压矢量的补偿进行控制。得推力环推力由PI控制器进行控制,根据推力的误差得出磁链角度的变化量,通过计算得出电压矢量控制电机。
控制结构框图如图2所示。电机速度的差值通过速度控制器输出电磁推力,与推力反馈的差值经过PI控制器得出定子磁链角度的变化量,与当前磁链的角度与定子磁链的幅值进行计算得出磁链的变化量,通过参考电压矢量计算得出参考电压,由空间矢量脉宽调制(space vector pulse width modulation,SVPWM)模块输出信号经逆变器对PMLSM进行控制。将磁链和推力滞环控制器用PI推力控制器进行了替代,可减小了磁链和推力的波动。本系统将传统PI速度控制器替换为基于Sigmoid函数的积分滑模速度控制器,在一定程度上对加强了系统的鲁棒性。
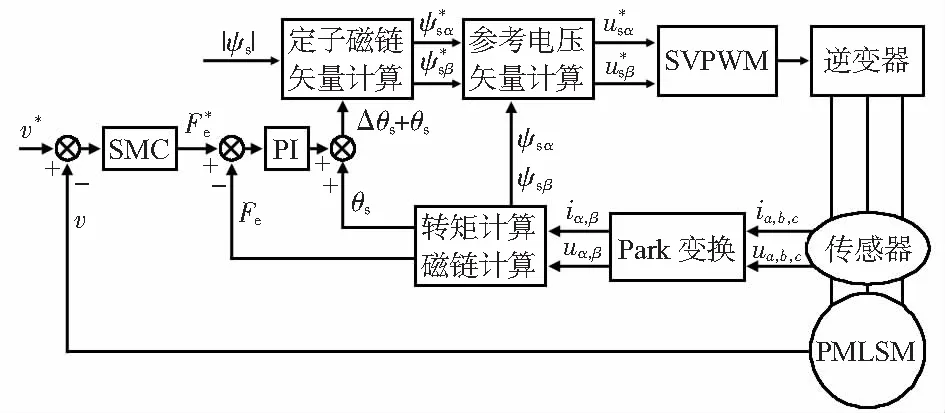
图2 控制结构框图
2 基于Sigmoid函数的积分滑模速度控制器设计
2.1 积分滑模速度控制器
传统的PI控制器有结构简单,易于实现等优点,但存在鲁棒性差等缺点。滑模控制可以弥补传统PI控制的不足之处[14]。
PMLSM机械运动方程为
(7)
式中M为电机运动质量;Fe为电磁推力;Fl为负载推力;B为阻尼系数[15]。将式(7)进行变形
(8)
取PMLSM的速度控制器的状态变量为
(9)
式中v*为PMLSM的参考速度,v为实际速度。
将式(7)和式(9)联立,得
(10)
式中F=Bv+ΔF,其中,ΔF为推力扰动。假设F有界,则|F|≤Fm。积分滑模面s设计为
式中c为参数,c>0。
滑模趋近律用指数趋近率模型
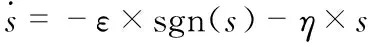
(12)
式中ε,η为常数。
设计积分滑模控制律为
(13)
定义李雅普诺夫函数为
(14)
可满足李雅普诺夫稳定性条件
=-ε×sgn|s|-η×s2≤0
(15)
根据李雅普诺夫稳定性,系统在滑模面以外的点都趋向于滑模面,会按照设定的规律到达滑模面,趋近速率取决于常数ε和η。
2.2 基于Sigmoid函数的积分滑模速度控制器
传统的滑模控制器会在系统进入滑模面切换时出现抖动。为了在一定程度上消除抖动,使用Sigmoid函数来替代切换函数。函数如式(16)所示
(16)
式中a值调节Sigmoid函数的斜度。a值与函数之间的关系如图3所示。由图3可以看出,a值越大,函数斜度越大,越接近开关函数,但不会像开关函数单值跳变,可以减小滑模控制器抖动。由式(13)可得基于Sigmoid函数的积分滑模速度控制器的控制率为
(17)
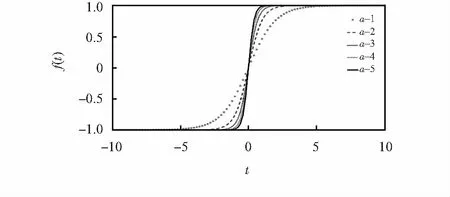
图3 Sigmoid函数
3 仿真实验
在MATLAB/Simulink中构建基于定子磁链角度计算的PMLSM的DTFC仿真实验模型。在t=0.5 s时加入了100 N的负载,且设置Sigmoid函数的a值为3。仿真实验结果如图4所示。由图4得,传统DTFC速度响应在0.3 s时刻到达稳态,超调量为8.75 %;在0.5 s时加100 N负载, 0.7 s时达到稳定。基于定子磁链角度计算的DTFC速度在0.18 s时刻到达稳态,超调量为2.25 %,超调量较小;在0.5 s时加100 N负载, 0.55 s时稳定。受到外界扰动时,速度暂态为0.05 s,小于传统DTFC的0.2 s,其抗干扰能力和鲁棒性更强,速度响应也强于传统的控制系统。
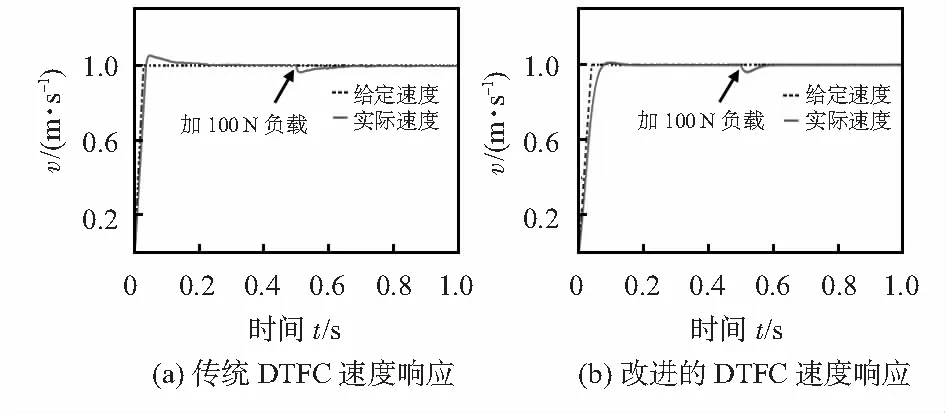
图4 速度响应曲线
由图5可得,传统DTFC推力响应在0.5 s时,加100 N负载,推力波动约在±15 N;当负载在0.5 s变为100 N时, 0.55 s时到达稳态。基于定子磁链角度计算的DTFC推力响应,在0.5 s时加100 N负载,0.5 s时速度达到稳定,波动约在±10 N,波动较小;当负载在0.5 s变为100 N时,推力在0.51 s时到达稳态。改进的控制策略推力波动更小,响应速度更快。
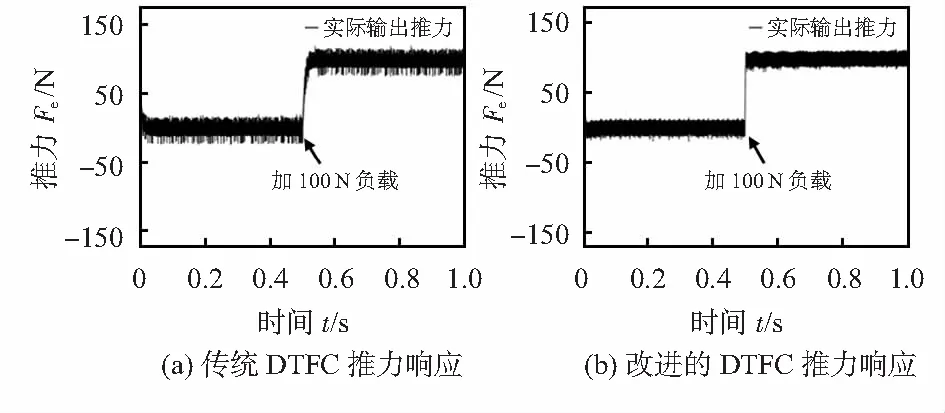
图5 推力响应曲线
由图6可得,传统DTFC磁链的变化范围在0.66~0.65 Wb之间;基于定子磁链角度计算的DTFC磁链变化的范围在0.653~0.657 Wb之间,改进的控制策略表现出抑制磁链波动的优点。由图7磁链轨迹可以看出,改进控制策略的磁链轨迹更加接近圆形,波动也较小。
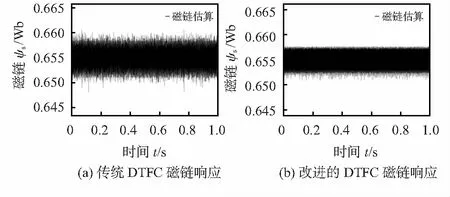
图6 磁链响应曲线
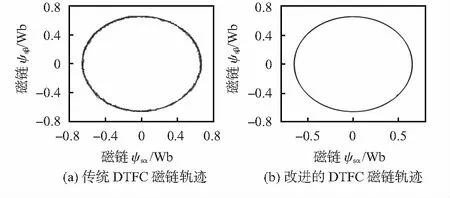
图7 磁链轨迹曲线
由图8可以看出传统DTFC启动时三相电流响应趋于稳定时间为0.25 s;基于定子磁链角度计算的DTFC三相电流响应趋于稳定时间为0.1 s,传统DTFC的启动电流大于改进后的控制策略,可得改进后的控制策略电机启动时的稳定性更强。
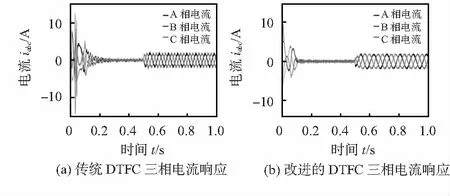
图8 三相电流响应曲线
电机参数表如表1所示。

表1 PMLSM主要参数
由上述分析可得,改进后的控制策略有效改善了传统DTFC推力和磁链的波动大的问题,在系统响应时间和抗干扰能力上也有一定的增强。
4 结 论
为改善传统DTFC易受扰动影响,推力和磁链波动大等缺点,设计了基于定子磁链角度计算的PMLSM直接推力控制。仿真实验表明:改进的直接推力控制相比于传统直接推力控制,推力和磁链波动小、鲁棒性强、速度响应快,有效改善了传统直接推力控制的不足。
