基于滑模磁链观测器的感应电机模型预测控制
2019-06-26孙佳将卢勇辉
孙佳将,卢勇辉,赵 金
(华中科技大学 自动化学院,武汉430074)
0 引 言
感应电机因其结构简单、价格低廉、运行可靠、可用于恶劣环境等优点,在生产与生活中得到了广泛的应用。近年来,有限控制集合模型预测控制作为一种新兴的高效控制策略被应用到感应电机的控制中,因其易于实现多变量控制和处理非线性约束的特性而受到关注[1]。有限控制集合模型预测控制通过系统状态预测的方法,利用设计好的目标函数直接控制磁链和转矩。因为预测过程需要使用电机的真实磁链,所以该方案对磁链观测的精度有很高的要求,而传统的电流模型磁链观测器和电压模型磁链观测器易受到电机参数变化的影响。
模型预测控制的磁链观测和磁链与转矩预测阶段均对电机参数存在依赖,特别是在磁链观测阶段,磁链观测的精度会直接影响下一步的磁链与转矩预测,进而影响到最终的目标函数选择。以闭环的磁链观测器替代传统的电流模型与电压模型可以很好地解决这一问题。而在常见的全阶磁链观测器、降阶磁链观测器、扩展卡尔曼滤波和滑模磁链观测器等闭环观测器中,滑模磁链观测器在提高参数鲁棒性上表现出最优越的性能[2-4]。
常规的滑模磁链观测器依据电流观测误差设计滑模控制函数,在实现对转子电阻变化的高鲁棒性的同时也引入了定子电阻变化的影响[5]。本文提出一种基于磁链观测误差的滑模控制函数设计方法,对滑模观测器的性能进行改进。因为磁链的真实值无法直接获取,磁链误差值以近似计算的方式得到。通过仿真和物理实验验证了该方案对电机参数变化的高鲁棒性。
1 感应电机模型预测控制
感应电机在静止两相正交坐标系中的数学模型为
(1)

模型预测控制基于电机方程(1)建立对应的预测方程。该方案的原理是,对应于逆变器可产生的8种电压矢量,通过预测在8种电压矢量作用下电机下一时刻的磁链和转矩,找到使目标函数值最小的电压矢量施加于系统,其中目标函数代表了磁链和转矩的最优化结果。
1.1 磁链估计
磁链估计是模型预测控制方案的第一步。传统的磁链估计方法包括电流模型和电压模型两种。考虑到电压模型直流误差累计的问题,通常采用电流模型对磁链进行估计。
(2)
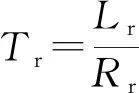
在得到转子磁链后,定子磁链由如下方程得到:
(3)

电流模型对定子电阻不敏感,但对转子电阻和电感敏感。当定子电阻或电感存在误差时,将会对磁链的估计产生影响。
1.2 磁链和转矩预测
磁链和转矩预测是感应电机模型预测控制的第二步。
定子磁链的预测模型通过电机的定子电压方程得到。将定子电压方程进行欧拉离散化可得:
(4)
式中,Ts为采样周期。
转矩预测模型通过电机的转矩方程通过欧拉离散化得到:
(5)
式中电流的预测模型通过电机的电流方程和磁链方程推导得到:
(6)

1.3 目标函数选择

目标函数的设计原理是,通过计算转矩和磁链的参考值与预测值的差值,在所有预测值中选择最接近于参考值的值。这样,逆变器的每一个开关周期都会产生使系统最接近控制目标的电压矢量。
(7)
式中,λ为权重因子。λ越大,表示磁链在控制目标中所占的比重越大。
权重因子一般表示为
(8)
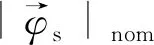
1.4 电机参数变化的影响
电机在正常运行条件下,等效电路的参数很难保持恒定不变。定子电阻和转子电阻的阻值会随温度发生变化,除了电机工作环境温度的影响外,电机在运行过程中也存在发热现象;同时,电机的趋肤效应也会导致电阻增加,漏电感减小。在感应电机的模型预测控制方案中,参数变化对磁链估计和控制量的预测都会产生影响,磁链估计阶段造成的估计误差也将直接影响到预测阶段。
本文以Matlab/Simulink的仿真环境对上述方案进行参数鲁棒性实验。仿真使用的电机参数如表1所示。在每次仿真实验中,通过修改Matlab电机模块中的某一项电机参数,来模拟实际电机参数的变化。参数的变化范围给定在50%~150%的标准值。仿真实验取两个极值进行仿真,即每一项电机参数的变化选择0.5倍的标准值和1.5倍的标准值进行验证。仿真实验给定的调速系统工作场景相同,使用感应电机的模型预测控制方案,给定转速500r/min,定子磁链给定0.6Wb。调速系统零负载起动,并在0.5s加50%额定负载(7Nm)。

表1 感应电机参数
图1~图3给出了电机的转子电阻和互感变化的情况下,电机的仿真结果。由于电流模型不依赖电机的定子电阻,本文未给出定子电阻的仿真曲线。
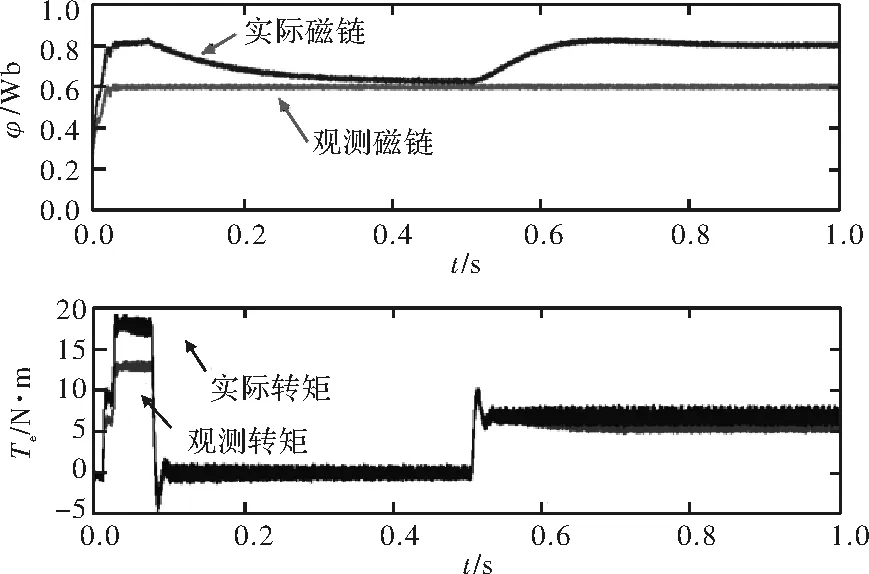
图1 转子电阻增大50%
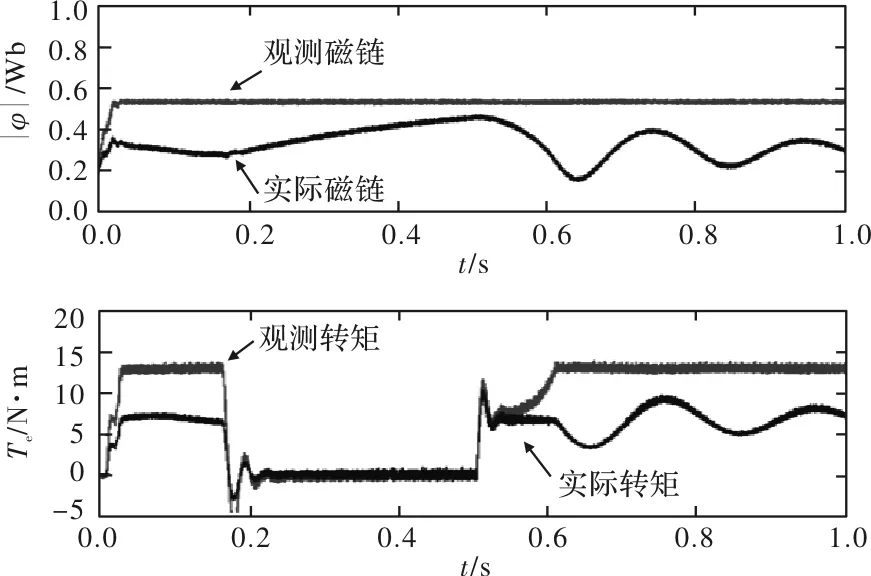
图2 转子电阻减小50%
转子电阻和互感的变化都会对磁链的观测结果造成影响。转子电阻增大时,实际磁链在7Nm负载下与真实磁链存在0.2Wb的误差,而在转子电阻减小的情况下,系统不稳定。互感变化对控制性能的影响相对较小,图3给出互感减小的情况下系统的仿真结果,在零负载情况下实际磁链与观测磁链之间产生0.3Wb的误差,增加7Nm负载后,该误差缩小到0.04Wb。

图3 互感增大50%

图4 互感减小50%
2 滑模磁链观测器
由于电流模型磁链观测器受电机参数变化的影响较大,本文提出一种感应电机滑模磁链观测器设计方案以提高对电机参数变化的鲁棒性。
滑模磁链观测器模型以感应电机数学模型为基础。以定子电流和转子磁链为状态变量,建立感应电机在αβ轴坐标系下的数学模型为
(9)
式中,isα和isβ为定子αβ轴电流,φrα和φrβ为转子αβ轴磁链,usα和usβ为施加在定子上的αβ轴电压。
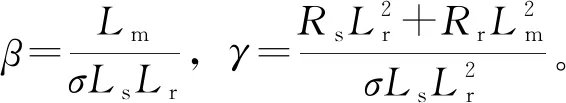
由于滑模磁链观测器的设计要以状态变量的观测值与实际值之差来建立滑模切换平面,而电机磁链的实际值无法直接得到,因此选择以电流的观测值和实际值的差值构建滑模切换面。
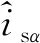
(10)
式中,Vα和Vβ为αβ轴上的滑模控制函数,该滑模控制函数基于电流观测误差进行设计,并选择常值切换控制的方式,形式上由一个符号函数和其正系数M组成,其表达式为
(11)
将观测器方程与电机方程作差,得到差值方程:
(12)
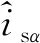
(13)
将式(12)代入式(13)可得
(14)
当M满足如式(15)所示条件时,可保证该极限值小于零。
(15)
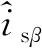
(16)
综上,当M同时满足式(15)和式(16)时,电流观测系统满足滑模可达性条件,观测状态量轨迹最终进入滑动模态。
(17)
将Vα和Vβ的等效值代入磁链误差方程,即可得到滑动模态时磁链观测误差的等效方程
(18)
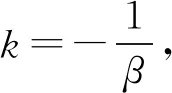
(19)
在上述设计方案中,以电流观测误差作为滑模切换面设计滑模控制函数,该方案能使电流的观测值很快的趋近于实际值,但对磁链的控制却是间接的,当电机定子电阻发生变化时,观测磁链仍无法很好地跟随真实磁链。本文提出一种基于磁链观测误差地滑模控制函数设计方法,对上述滑模磁链观测器设计方案进行改进。
在式(10)的滑模磁链观测器方程中,加入新的滑模控制函数Uα和Uβ
(20)
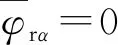
(21)

(22)

(23)
而最终改进后的滑模磁链观测方程为
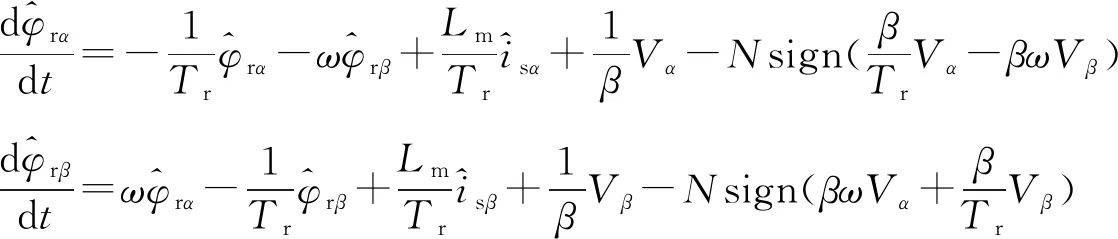
(24)
N的取值需要考虑两方面的因素,第一,N值需要保证Uα和Uβ能使磁链观测值进一步趋近于其真实值,因此同样需要满足滑模可达性条件;第二,N的取值不宜过大,导致Uα和Uβ本身设计所带来的误差被放大。可通过仿真实验选取出最合适的N值。
滑模磁链观测器的Matlab/Simulink仿真结果如图5~图10所示,分别给出了定子电阻、转子电阻和互感变化的情况下电机的磁链观测结果。

图5 定子电阻增大50%

图6 定子电阻减小50%

图7 转子电阻增大50%

图8 转子电阻减小50%

图9 互感增大50%
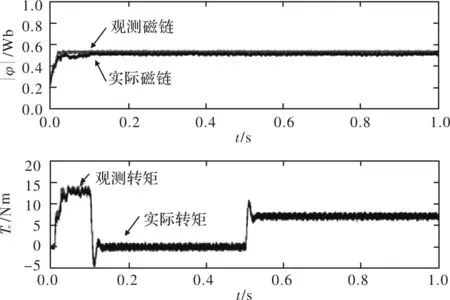
图10 互感减小50%
3 物理实验
物理实验包括控制性能实验和参数敏感性实验两部分。
模型预测控制的阶跃响应实验结果由图11给出。感应电机给定转速500r/min,带5Nm负载起动。 滑模磁链观测器在参与调速系统控制的情况下,对系统的稳态响应性能未造成明显影响。虽然滑模磁链观测器本身会带来抖振问题,但最终转速曲线能很好地控制在500r/min的转速给定,其波动在正负4r/min。磁链观测值很好地控制在0.6Wb,转矩观测值在5Nm,与实际输出转矩一致。
在物理实验中,无法对真实电机的物理参数进行修改。因此,此处滑模磁链观测器的参数敏感性实验采用反向的设定方式,通过修改滑模磁链观测器中使用的电机参数来造成观测器与电机的参数误差,从而判断在存在参数误差的情况下系统的控制性能。参数敏感性实验结果以转子电阻变化为例给出。图12和图13分别给出了滑模磁链观测器中转子电阻增大50%和减小50%的实验结果。实验结果显示,当系统存在参数误差时,调速系统的控制性能未受到很大的影响,依然表现出很好的稳态控制性能。
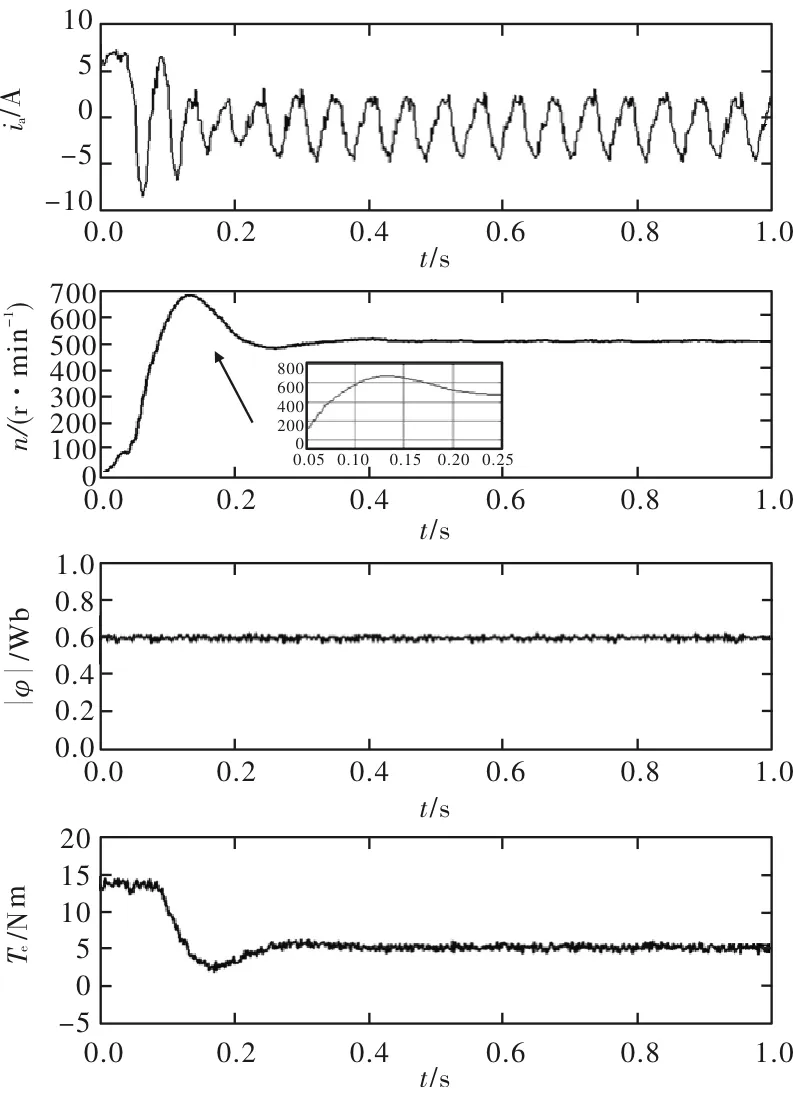
图11 感应电机模型预测控制阶跃响应曲线

图12 滑模磁链观测器中转子电阻增大50%

图13 滑模磁链观测器中转子电阻减小50%
当滑模磁链观测器中转子电阻增大50%时,转速存在正负5r/min的波动,定子磁链控制在给定值0.6Wb,转矩预测也接近实际输出转矩7Nm。当滑模磁链观测器的转子电阻减小50%时,其动态性能受到一定程度的影响,进入稳态后,速度保持在500r/min,存在正负4r/min的波动,磁链被控制在0.6Wb的给定值,而观测转矩比实际输出转矩偏大。
4 结 论
本文以提高感应电机模型预测控制对电机参数变化的鲁棒性为目的,设计了感应电机的滑模磁链观测器,针对常规滑模磁链观测器无法实现对定子电阻参数鲁棒的问题,设计基于磁链观测误差的滑模控制函数对观测器性能进行改进。仿真和实验结果表明,本文设计的滑模磁链观测器对电机参数变化具有很好的鲁棒性,大大提高了感应电机模型预测控制的在电机参数变化情况下的控制性能。
