初中数学“数学运算”素养测评的实践探索

摘要：数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养。在2020年江苏省义务教育学业质量监测中，初中数学项目组以课程标准为测评工具研制依据，结合数学核心素养具体评价指向，改变单纯考查数学内部纯粹计算的命题思路，将考查知识、技能与考查对运算的理解和应用相结合，并借助于访谈、多轮试测等手段，提高测评的科学性。

关键词：数学运算;学业质量监测;素养测评;初中数学

本文系江苏省教育科学“十四五”规划重点课题“指向育人方式变革的初中数学体验教学模式建构研究”（批准号：B/2021/02/02）的阶段性研究成果。一、 数学运算素养测评的实践依据

（一） 数学运算的内涵和表现

《普通高中数学课程标准（2017年版）》对“数学运算”的描述为：“数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养。主要包括：理解运算对象，掌握运算法则，探究运算思路，选择运算方法，设计运算程序，求得运算结果等。数学运算主要表现为：理解运算对象，掌握运算法则，探究运算思路，求得运算结果。”

（二） 数学运算的评价要素

相对于知识技能，素养更具有内隐性，在具体内涵和表现机制上也更为复杂。素养是个体内在的能力、品格或特征，它指向个体在简单或复杂情境中的外在表现，但其本身并不等同于这种表现。素养无法直接观测，但可以通过学生在指令性任务中的实际表现加以推测。因此，建立数学运算素养与评价任务间的正向关联，是评价的重要内容，这种评价要结合教学的载体、文化的背景、未来的发展等要求。基于数学运算的内涵和表现以及初中生的认知水平，我们厘定了数学运算素养的评价要素，包括：明晰运算的对象和意义，理解算法与算理之间的关系，掌握关联的运算法则，寻找与探究运算方向，选择合适的运算方法，设计有效的运算程序，正确、迅速、灵活地完成运算。

二、 数学运算素养测评的表现水平

（一） 对法则和运算等认识清晰，根据具体题目的特殊性正确选择法则和运算律

1. 水平描述

水平A：能够在科学和社会情境中发现运算问题，确定运算对象，明晰算理，灵活选择运算法则，探究运算方向。

水平B：能够在数学情境中明晰运算对象，提出运算问题，探究运算方向和目标。

水平C：能够在简单的数学情境中理解运算对象，提出运算问题，建立运算关系。

水平D：不能在数学情境中理解运算对象，提出运算问题，建立运算关系。

2. 相关示例

李奶奶买了一筐草莓，连筐共重a kg，其中筐重1 kg。将草莓平均分给4位小朋友，每位小朋友可分得（）

A. a4kgB. a4-1kg

C. a+14kgD. a-14kg

（二） 合理、简洁地设计程序，正确、迅速地完成运算，通过运算解决问题

1. 水平描述

水平A：能够针对运算问题，合理构造运算程序，并以此为基础建立合理、简洁的解决问题模式。

水平B：能够针对运算问题，正确分析运算条件、确定运算方向，合理选择运算方法，正确利用运算解决问题。

水平 C：能够理解法则的背景和适用范围，掌握基本的运算法则，根据数学问题的特征选择合适的运算法则解决问题。

水平D：不能理解法则的背景和适用范围，不能掌握基本的运算法则，不能根据数学问题的特征选择合适的运算法则解决问题。

2. 相关示例

如图1，风筝牵引绳AB的长度所在范围是（）

A.36m至38mB. 38m至40m

C. 40m至42mD. 42m至44m

三、 数学运算素养测评的研究思路

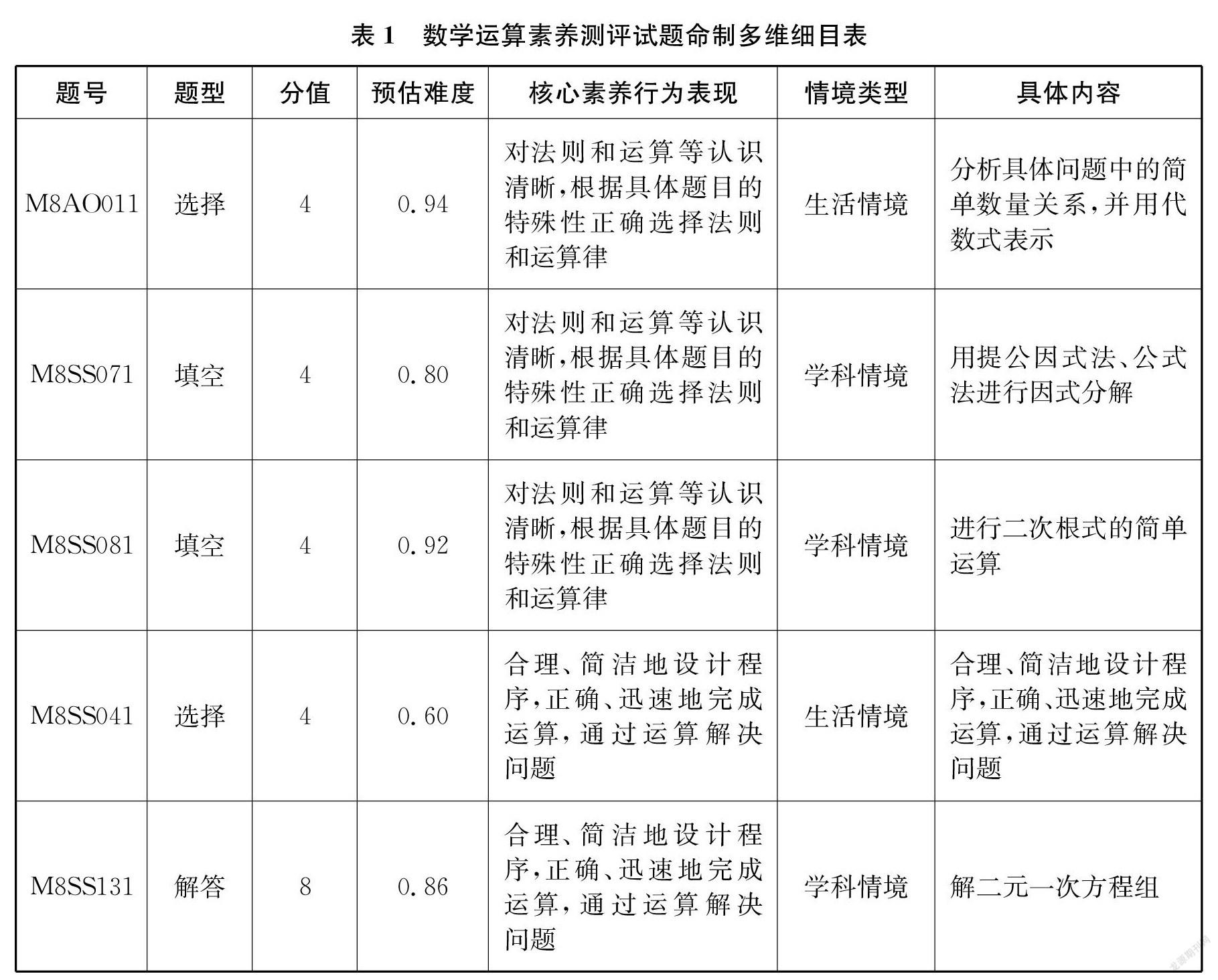
下页表1所示即为2020年江苏省义务教育学业质量监测中数学运算素养测评试题命制的多维细目表，凸显了数学运算素养测评的研究思路。

四、 数学运算素养测评的试题改进

2020年江苏省义务教育学业质量监测中关于数学运算素养的测评共5小题24分。本文以M8SS041为例，具体说明数学运算素养测评试题的改进过程。

该题重点考查“合理、简洁地设计程序，正确、迅速地完成运算，通过运算解决问题”的数学运算素养，要求学生用有理数估计一个无理数的大致范围。该题结合学生熟知的生活情境进行考查。

（一） 试题初稿及说明

如下页图2，要使风筝牵引绳与船面成45°角，并使风筝的垂直高度为150m，需要用绳子的长大约为（）表1数学运算素养测评试题命制多维细目表

题号题型分值预估难度核心素养行为表现情境类型具体内容M8AO011选择40.94对法则和运算等认识清晰，根据具体题目的特殊性正确选择法则和运算律生活情境分析具体问题中的简单数量关系，并用代数式表示M8SS071填空40.80对法则和运算等认识清晰，根据具体题目的特殊性正确选择法则和运算律学科情境用提公因式法、公式法进行因式分解M8SS081填空40.92对法则和运算等认识清晰，根据具体题目的特殊性正确选择法则和运算律学科情境进行二次根式的简单运算M8SS041选择40.60合理、简洁地设计程序，正确、迅速地完成运算，通过运算解决问题生活情境合理、简洁地设计程序，正确、迅速地完成运算，通过运算解决问题M8SS131解答80.86合理、简洁地设计程序，正确、迅速地完成运算，通过运算解决问题学科情境解二元一次方程组

A. 173mB. 212m

C. 285mD. 300m

该题要求学生掌握等腰直角三角形的三边关系，会进行初步的估算。300人试测后，我们做了访谈。设计的访谈问题是：（1） 你选的答案是什么？你是怎么得出的？ （2） 2大约是多少？你是如何知道的？学生的回答有：这个三角形是等腰直角三角形，利用勾股定理可得风筝牵引绳长度的平方是45000，再找接近的答案;根据图形可以判断三角形是等腰直角三角形，利用勾股定理求得风筝牵引绳长度的平方是45000，再分别计算173、212、285、300的平方，发现最接近的数是212;只要长度的平方比45000大都可以，因為风筝牵引绳在船上可能也有一部分;数字太大了，怎么算都不对。可见，初稿求风筝牵引绳长度的选项设置有歧义，不够严谨;数据设置过大，与实际情况有出入。

（二） 试题过程稿及说明

如下页图3，风筝牵引绳的长度值所在范围可能是（）

A. 36至38mB. 38至40m

C. 40至42mD. 42至44m

项目组经过多轮讨论，完善了题目的表述方式，在图形上增加了字母A与B，在题干中增加了牵引绳AB的明示，形成了试题的最终稿。

（三） 试题定稿及说明

如图4，风筝牵引绳AB的长度所在范围是（）

A. 36m至38mB. 38m至40m

C. 40m至42mD. 42m至44m

从全省监测数据来看，该题学生的得分率为0.55，与预设难度稍有差距。在访谈过程中，对于“在整份试卷中，你对哪些试题比较感兴趣？”这一问题，有多位学生选择了该题，反映了学生对该类数学运算素养考查的

载体很有兴趣。

在2020年江苏省义务教育学业质量监测中，初中数学学科以课程标准为测评工具研制依据，结合数学核心素养具体评价指向，改变单纯考查数学内部纯粹计算的命题思路，将考查知识、技能与考查对运算的理解和应用相结合。数学运算素养的测评旨在通过学生在具体任务中的表现，推断其在数学运算素养方面的表现水平，这一推断过程会比传统测评方式更为复杂，结果更具不可预测性。这就要求我们准确把握数学运算素养的内涵和表现，创设能够引发数学运算素养表现的评价任务，以学业质量标准为依据，研制等级性、多元化的测评工具，同时借助访谈、多轮试测等手段，提高测评的科学性。

参考文献：

[1] 中华人民共和国教育部. 普通高中数学课程标准（2017年版）[S].北京：人民教育出版社，2018.

[2] 中华人民共和国教育部.义务教育数学课程标准（2011年版）[S].北京：北京师范大学出版社， 2012.

[3] 义务教育学科核心素养与关键能力研究项目组.义务教育学科核心素养·关键能力测评与教学（初中数学）[M].南京：江苏凤凰科学技术出版社，2018.（周雪兵，江苏省南京市金陵汇文学校，特级教师，正高级教师。）