初中数学“逻辑推理”素养测评的实践探索

摘要：逻辑推理是指从一些事实和命题出发，依据规则推出其他命题的素养。在2020年江苏省义务教育学业质量监测中，初中数学项目组改变逻辑推理素养的测评单纯在数学内部情境中命题的思路，从单纯考查数学知识到同时考查数学知识与数学核心素养的发展。在注重问题解决、关注基础知识和基本技能掌握的同时，结合个体与综合、复杂任务情境的有效互动，通过数学思考和表达来考查学生的数学核心素养。

关键词：逻辑推理;学业质量监测;素养测评;初中数学

一、 逻辑推理素养测评的实践依据

（一） 逻辑推理的内涵和表现

《普通高中数学课程标准（2017年版）》对“逻辑推理”的描述为：“逻辑推理是指从一些事实和命题出发，依据规则推出其他命题的素养。主要包括两类：一类是从特殊到一般的推理，推理形式主要有归纳、类比;一类是从一般到特殊的推理，推理形式主要有演绎……逻辑推理主要表现为：掌握推理基本形式和规则，发现问题和提出命题，探索和表述论证过程，理解命题体系，有逻辑地表达与交流。”

（二） 逻辑推理的评价要素

数学核心素养评价要素构建的理念是培养社会发展和公民发展必需的素养，鼓励学生在学习数學知识的同时，将其运用于现实生活。因此，数学核心素养测评试题需要具有如下特征：内容指向学生的数学核心素养;能对学生的素养水平进行判断，对学生是否具备适应当前及未来社会的素养进行测评;契合数学教育的实际，贴合我国数学教育文化背景，且与未来社会发展所需要的素养接轨。基于逻辑推理的内涵和表现以及初中生的认知水平，我们厘定了逻辑推理素养的评价要素，包括：掌握逻辑推理的基本形式，表述论证的过程;在解决问题的过程中，形成有论据、有条理、合乎逻辑的思维品质;能发现问题和提出命题;理解数学知识之间的联系，建构知识框架;在解决问题的过程中，形成合情推理的思维品质。

二、 逻辑推理素养测评的表现水平

（一） 从已有的事实（包括定义、公理、定理等）和确定的规则（包括运算的定义、法则、顺序等）出发，按照逻辑推理的法则证明和计算

1. 水平描述

水平A：能掌握逻辑推理的基本形式，表述论证的过程;在解决问题的过程中，形成有论据、有条理、合乎逻辑的思维品质。

水平B：能表述证明的过程;在解决问题的过程中，发展自身的逻辑推理能力。

水平C：能基本完成证明的过程;在解决问题的过程中，形成逻辑推理的意识。

水平D：不能完成基本证明;在解决问题的过程中，缺乏逻辑推理的意识。

2. 相关示例

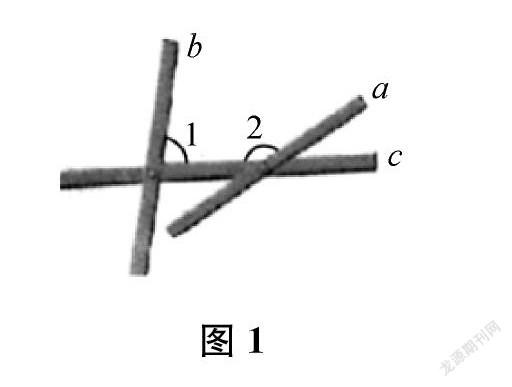
如图1，固定木条b、c，使∠1=80°。旋转木条a，要使得a∥b，则∠2应调整为（）

A. 100°B. 90°C. 80°D. 70°

（二） 从已有的事实出发，凭借经验和直觉，通过归纳和类比等推断某些结果

1. 水平描述

水平A：能发现问题和提出命题;能理解数学知识之间的联系，建构知识框架;在解决问题的过程中，形成合情推理的思维品质。

水平B：能发现一些问题;能体会数学知识之间的联系;在解决问题的过程中，发展自身的合情推理能力。

水平C：能发现一些简单的结论;能了解数学知识之间的简单联系;在解决问题的过程中，有合情推理的意识。

水平D：不能发现结论;不能了解数学知识之间的联系;在解决问题的过程中，没有合情推理的意识。

2. 相关示例

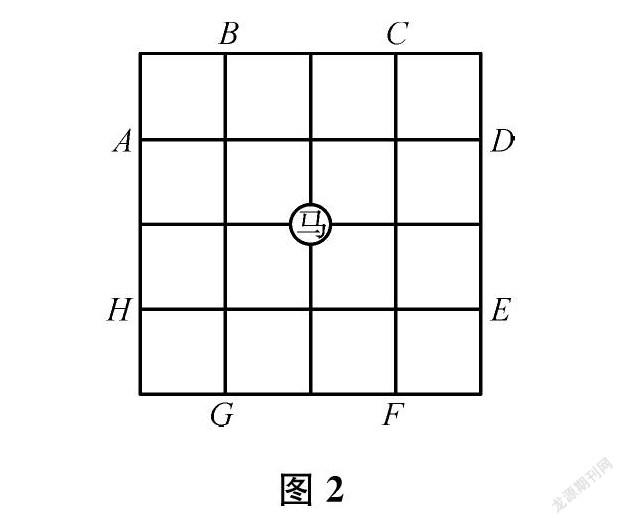
中国象棋是中华民族的文化瑰宝，它历史久远、博大精深。如图2，“马”走一步可到达A、B、C、D、E、F、G、H中的某一个位置，俗称“马走日”。在如图3所示的象棋盘中，“马”至少走步能到达“帅”的位置。

三、 逻辑推理素养测评的研究思路

长期以来，对学生学业质量的评估遵循的是“教知识、考知识”的逻辑，这种逻辑以知识的教学作为起点和归宿。此次学业质量监测对逻辑推理素养的测评，形式上与以前的考试大同小异，但内容上淡化了单纯对知识点理解和掌握情况的考查，增加了对能力因素的考量;改变了单纯在数学内部情境中命题的思路;淡化了模式化的收敛性题型，将情境性、开放性、发散性问题融入监测中。

表1即为2020年江苏省义务教育学业质量监测中逻辑推理素养测评试题命制的多维细目表。

四、 逻辑推理素养测评的试题改进

2020年江苏省义务教育学业质量监测中关于逻辑推理素养的测评共6小题24分。本文以M8AS151、M8AS152（为同一大题的2个小问）为例，说明逻辑推理素养测评试题的改进过程。

00该题要求学生“从三角形全等的判定定理出发，分析全等的条件，按照已有的定理进行证明”及“从全等三角形的性质出发，分析数量关系及位置关系，按照已有的定理或法则进行计算”。综观对“三角形全等判定”与“全等三角形性质”知识点的考查，多处在以学科语言、符号、图形为主要特征的学科情境下，学生对问题的解决往往凭经验、凑条件、套模式，感受不到学以致用的乐趣。机械套用解题程序和步骤解答的试题无法考查学生的数学核心素养，只有在综合、复杂的任务情境中，促进个体完成数学思考和数学表达的试题才能较好地考查学生的数学核心素养。设计一个能够让学生有效推理的情境，用问题逐步引导、驱动学生思考，体现学生的逻辑推理素养水平，是我们编制该题的初衷。

（一） 试题初稿及说明

小丽与爸爸妈妈在操场上荡秋千。如下页图4，小丽坐在秋千上的A处，两脚在地面上使劲一蹬，妈妈在1.2米高的B处接住她，使劲儿一推，爸爸在1.6米高的C处接住她。若妈妈与爸爸之间的水平距离为4米，∠BOC=90°。

学科情境根据三角形全等解决实际问题图4

（1） 请你在图中构造一对全等的三角形（要求：指出这对全等三角形，并简要地描述构造方法）

（2） B、C两点到OA的水平距离分别是多少？

该题围绕图形学习的3个基本步骤（定义、判定、性质）展开。每个步骤的设计遵循自然生长的原则。在生活情境中，调动学生的已有经验：在荡秋千的过程中，秋千板位置改变了，但是秋千绳的长度不变。这就是一个推理，OA=OB=OC。

在30人测试访谈中，我们设计了如下问题：1.你的答案是什么？说说你的分析过程。（了解学生是观察得出结论，还是根据条件推导得出结论的）2.你玩过荡秋千吗？3.你的生活经验对做这一题有帮助吗？体现在哪里？4.你喜欢做直接证明的题目，还是像这样有生活背景的题目？

学生给出的比较集中的结论有：1.我喜欢做这类題目，不难，平时玩过荡秋千，感觉有帮助，知道OA=OB=OC。2.不清楚第（1）问中“在图中构造一对全等的三角形”，是不是一定要与解决第（2）问时用到的全等三角形一致。

学生的访谈引发了项目组对命题的进一步思考：第一，真实的情境在解决具体问题的过程中起到了正迁移的作用，因为学生有荡秋千的经历，所以能判断出OA=OB=OC这一关键信息。第二，第（1）问构造一对全等三角形，学生会任意构造，偏离预设;第（2）问的结论要基于第（2）问全等的判定。

（二） 试题过程稿及说明

小丽与爸爸妈妈在操场上荡秋千。如图5，小丽坐在秋千上的A处，两脚在地面上使劲一蹬，妈妈在1.2米高的B处接住她，使劲儿一推，爸爸在1.6米高的C处接住她。若妈妈与爸爸之间的水平距离为4米，∠BOC=90°。

（1） △CGO与△OFB全等吗？请说明理由。

（2） B、C两点到OA的水平距离分别是多少米？

修改后，为了将第（1）问与第（2）问建立联系，本来开放性的问题变得聚焦于一对具体的全等三角形，CG、BF两条垂线段直接标示在图中，降低了题目难度，不符合多项细目表的要求;CG、BF两条垂线段与情境不能一一对应，导致对学生逻辑推理能力的考查体现不足。

（三） 试题定稿及说明

小丽与爸爸妈妈在公园里荡秋千。如图6，小丽坐在秋千的起始位置A处，OA与地面垂直，两脚在地面上用力一蹬，妈妈在距地

面1.2 m高的B处接住她后用力一推，爸爸在C处接住她。若妈妈与爸爸到OA的水平距离BF、CG分别为1.8m和2.2m， ∠BOC=90°。

（1） △CGO与△OFB全等吗？请说明理由。

（2） 爸爸是在距离地面多高的地方接住小丽的？

定稿试题的图中去掉了由B、C两点向地面作的两条垂线，问题改为生活情境中的语言“爸爸是在距离地面多高的地方接住小丽的”。学生思考这一问题需经历从现实空间中抽象出垂线段的过程，将距离转化为图中线段的和或差，是逻辑推理素养的具体体现。

该题情境贴近学生的生活经验，学生读题的过程即生活场景的再现;学生将生活语言转化为符号语言，将数学知识应用于生活，是对三角形全等判定和全等三角形性质考查的一个突破。从全省监测数据来看，2个小问学生的得分率分别为0.76和0.61，与预设难度基本吻合。

综上，在2020年江苏省义务教育学业质量监测中，初中数学项目组改变逻辑推理素养的测评单纯在数学内部情境中命题的思路，从单纯考查数学知识到同时考查数学知识与数学核心素养。在注重问题解决、关注基础知识和基本技能掌握的同时，结合个体与综合、复杂任务情境的有效互动，通过数学思考和表达来考查学生的数学核心素养。

参考文献：

[1] 中华人民共和国教育部.普通高中数学课程标准（2017年版）[S].北京：人民教育出版社，2018.

[2] 史宁中.数学基本思想18讲[M].北京：北京师范大学出版社，2016.

[3] 陈蓓.高中生数学核心素养评价指标研究[J].教育研究与评论（中学教育教学），2019（9）.

[4] 义务教育学科核心素养与关键能力研究项目组.义务教育学科核心素养·关键能力测评与教学（初中数学）[M].南京：江苏凤凰科学技术出版社，2018.

[5] 喻平.数学关键能力测验试题编制：理论与方法[J].数学通报，2019（12）.（李贺，江苏省徐州市教育科学研究院。徐州市名教师、领军名师。曾获全国和江苏省青年教师优质课评比一等奖，江苏省网络团队教研比赛一等奖。）