设置问题深入探究 提升数学素养
2021-08-26黄李华


摘 要:数学素养是学生核心素养的重要组成部分,是学生发现问题、分析问题、解决问题的能力。它能充分展示学生的数学观点、数学思维、数学方法等。设置问题、深入探究是培养学生数学素养的主要方式,也是初中数学教师开展教学工作的主要手段。因此,教师要针对学生的学习过程精心设计问题,引发他们去思考、去探究,在激活他们数学思维的同时,提升其数学综合能力。
关键词:初中数学;数学素养;问题
中图分类号:G427 文献标识码:A 文章编号:2095-624X(2021)12-0055-02
引 言
在传统的数学教学模式中,教师以讲解为主,学生以识记为主;提问不够,探究不够,不利于学生数学核心素养的生成。基于此,教师要改变教学方式,以学生为主,以问题为驱动,以探究为中心任务,不断促进学生数学素养的提升。
一、借助问题,在探究中找寻规律
探究的目的,不仅仅是一般意义上的解决问题,更是发现规律,让更多的问题得到解决。换言之,教师教学的视角不能仅仅停留在解决问题上[1]。教师在课堂上的提問,应促进学生的进一步探究,为他们提供思考的方向。以新苏教版七年级上册“角度的计算”一课为例,教师如果能让学生在问题中探究出一些基本的图形,再让他们形成一些常用的结论,就会为他们之后的深度探究奠定坚实的基础。比如,三角形的内角和定理及外角性质定理是解决三角形中有关角的证明与计算问题的常用知识。
【片段一】鱼尾形和X形的应用
例1:图1是一个五角星ABCDE,求∠A+∠B+∠C+∠D+∠E的度数。
师:大家仔细观察五角星图形,说说能看出什么。
生1:图中有多个鱼尾形状的四边形,如鱼尾四边形ACOD,鱼尾四边形BDPE等。
师:你们是怎么定义鱼尾形状的四边形的。
生2:像鱼尾一样凹的部分称之为鱼尾四边形。
生3:我一共可以找出5个鱼尾四边形。
师:找鱼尾四边形有什么用呢?
生:如图2所示,在鱼尾四边形ABCD中,∠DCB=∠A+∠B+∠D。只要连接AC,这样的结论就是显而易见的。我们可以把这样的总结为鱼尾角的性质,利用鱼尾角性质易求∠A+∠B+∠C+∠D+∠E=180°.
在教学过程中,教师要让学生沿着问题去寻找题目中的共性,在共性中探究,从而突破学习难点,逐步提升数学素养。此题属于“星形”问题,含有多个三角形,探究中要求的角不在同一个三角形中,可用鱼尾形把要求的角集中到一个三角形中,这样做起到了化零为整的效果。
【片段二】A形和X形的应用
开展探究活动的目的是开阔学生的视野,让他们不断总结新的规律,不断在问题抛出的基础上有新的探究。学生能探究出鱼尾状图形的角度关系,也会继续思维的脚步。教师可设置适当的题目,进行一定的引导。
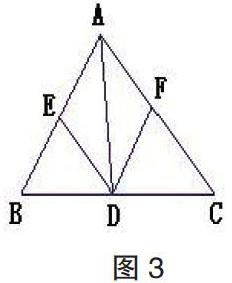
例2:如图3所示,在△ABC中,∠BAC=60°,D、E、F分别是BC、AB、AC上的点,∠B=∠DEB,∠C=∠DFC。求∠EDF的度数;若D、E、F分别在三边的延长线上,其他条件不变,求∠EDF的度数。
教师先提问学生图3中的这些图形有什么样的规律,并让学生进行观察。学生发现,图中有两个A形,即△ BDE与△BCA,△CDF与△CBA;很明显,它们有一个公共的顶角,拥有一对平行线,所以两对同位角相等。于是学生考虑使用A形图的结论,同时他们还发现其中涉及的∠BDE、∠CDF又和要求的∠EDF构成平角。顺着教师的问题,学生发现点D、E、F的位置发生变化后,图中出现一个A形和一个X形。由图可知,X形的特点与性质:一对平行线、中间为对顶角、两个内错角相等,因而可以考虑利用A形和X形的结论。最后可整理出∠EDF与∠BAC的数量关系,从而求出∠EDF的度数。显而易见,学生的数学素养在发现规律、利用规律的过程中得到了不断提升。
二、借助问题,在探究中找寻关联
初中生需要探究的数学知识有很多,因而教师可以让学生在日常的学习中养成探究的习惯,进而在深度学习的同时,形成新的数学素养。比如,在学习完新苏教版九年级上册“二次函数”后,学生就可以探究二次函数与几何图形之间可以进行怎样的变换。一方面,以二次函数为背景的几何图形的变换问题是近几年考试中的热点题型;另一方面,对于这类题目的探究又能培养学生多方面的能力,如综合能力、分析能力、推理能力等。
例3:如图4所示,在平面直角坐标系中,矩形OABC的边OA、OC分别在y轴和x轴的正半轴上,且长分别为1,4,D为边AB的中点,一抛物线经过点A、D及点F(-1,-2)。(1)求抛物线的解析式;(2)把△OAD沿直线OD折叠后点A落在点A'处,求点A'的坐标。
学生可以以小组为单位,结合题目,参考结论,寻找关联。最后学生发现一定要用到的二次函数的一般形式,即y=ax2+bx+c(a、b、c是常数,a不为0),但题目没有提到,还有可能要用到勾股定理,即如果直角三角形的两条直角边长分别为a,b,斜边为c,那么a2+b2=c2,题目也没提到。这样的探究既能让学生在问题中找寻关联,又能让学生在探究中学会分析。
对于题目中的第一问,学生这样探究:已知点F(-1,-2),要求解析式,说明还要找到另外的两个点,根据题意可知,点A和点D 的坐标分别是(0,1)(2,1)。对于第二问,学生的探究就成了寻找关联,求点坐标其实就是求线段的长,而求线段的长其实就是根据勾股定理列方程。可见,探究的目的就是不拘一格地提升学生的数学核心素养,锻炼学生多方面的能力。
三、借助问题,在探究中进行分类
探究在问题中产生,也在问题中发展,是数学学习的一种姿态。对于探究而言,它需要一定的严密性与完整性。因此,在教学过程中,教师可以借助问题培养学生在探究中养成分情况讨论的习惯。
例4:如图5所示,已知直线y=x+1与y轴交于A点,与x轴交于点D,抛物线y=x2-x+1与直线交于A、E两点与x轴交于B、C两点。设动点P在x轴上移动,当△PAE是直角三角形时,求点P的坐标。
学生先是进行独立探究,由直线y=x+1与y轴交于A点,与x轴交于点D,求得A(0,1),D(2,0)。同时,学生又由抛物线y=x2-x+1与直线交于A、E两点,在解方程组的过程中求得E(4,3)。
当学生再看△PAE是直角三角形时,发现如果顶点不固定可能情况不一样,产生了疑虑。这时,教师要给学生时间,让他们自由探究。学生自主地进行了小组合作,将题目分为三类情况进行了探究。首先,学生以点A为直角顶点,接着他们以点E为直角顶点,最后他们以点P为直角顶点。
结 语
在初中数学教学中,教师要巧创设问题,给学生以不断探究的空间,从而让他们的个性得到充分发展,进而促进其素养的生成。同时,学生要成为问题设置的受益者、探究环节的主导者,最后成为素养的开拓者。
[参考文献]
刘会影.谈初中数学课堂如何“以问题引领深度学习”[J]. 中学数学,2020(12):75-76.
作者简介:黄李华(1977.10—),男,江苏启东人,本科学历,中学一级教师,研究方向:初中数学教学。
