初中学生几何直观能力培养策略研究

曹娅烨

摘 要： 直观是一个人通过观察对事物表象的直接判断.数学学科中的空间几何等内容的学习，需要学生具备几何直观能力，通过对初中生的几何直观能力培养，可以提升学生对图形表象以及表面意义的直接感知，以帮助学生理解图形中所蕴含的深层次意义，帮助学生发现图形表象及其内在之间存在的隐含信息，从而让学生的数学几何直观问题能力得以提升.基于此，本文分析了数学几何直观能力培养应遵循的原则，并重点阐述了初中数学教学中的几何直观能力培养有效策略，以供参考.

关键词： 初中数学;几何直观能力;培养

中图分类号： G632       文献标识码： A       文章编号： 1008-0333（2021）35-0008-02

人们普遍认为，在数学学习中能够成功地解决问题是十分重要的，但是学生在学习中具备发现问题的能力更为重要，学生在问题发现的过程中，可以透过对事物的直观观察获得意料之外的启发.因此，数学教师应关注对初中生的几何直观能力培养，认识到几何直观能力的形成，不仅仅是初中生必须具备的数学能力，同时也是衡量初中生对数学知识掌握情况的标准，是“教”与“学”的基本交互活动.当学生具备较高水平的几何直观能力时，其对数学定义、定理的理解与吸收程度会有所提升，数学思维能力会得到锻炼，教师应结合学情以及数学学科特点，对初中生进行几何直观能力的培养，以促进数学教学整体质量的提升.

一、数学几何直观能力培养应遵循的原则

1.创新性

传统的数学课堂中，教师对几何直观能力培养所运用的教学方法相对单一，而在教育新时代发展的背景下，教师应做到创新性地教学，能够利用先进的教学技术创新几何直观能力培养的方法，发挥出教育新技术的优势，打破传统课堂的局限性，善于借助新型的教学方法与教学技术吸引初中生的注意力，让学生在好奇心的促使下，更加积极主动地参与到数学学习活动中，以获得几何直观能力的锻炼.

2.引导性

虽然与小学生相比，初中生在观察与思维能力方面已经得到了一定程度上的提升，但是仍处于发展阶段，在发展的过程中需要教师的引领以及同伴的帮助.因此，教师在数学教学中应发挥出自身的引领作用，扮演学生学习与发展中的领路人，能够在学生学习需要时给出启示，通过教师的引领以及同伴的参与，促使初中生获得独特的感官体验，开发学生的空间思维以及洞察能力等.因此，在数学几何直观能力的培养中，需要教师遵循以学生为主体、以教师为主导的原则，正确定义“教”与“学”的关系，才能保障几何直观能力培养目标的实现.

3.拓展性

初中数学教材的编写是经过众多专家精挑细选的，所遵循的是课程改革的精神，也为教师的数学教学指明了方向，但是教材在编写中受到多种因素的制约，其中所收纳的内容是有限的，为了更好地助力初中生的几何直观能力发展，需要教师以教材内容为依据，适当地开发课本之外的优质教学资源，以拓展与延伸学生的学习视野，以丰富的教学资源运用，满足不同层次学生的发展需求.

二、初中数学教学中的几何直观能力培养有效策略

1.借助生活实物，树立几何直观意识

从不同年龄段学生的思维发展规律角度分析，可以发现初中生正处于具象思维向抽象思维发展的时期，但是此时的初中生在学习中依然以具象思维为主，也就是说直观的、具体化的实物观察，更加符合初中生的思维发展特点，也能够透过对具体的实物观察，刺激学生的感官体验，从而引领学生建立起实物与几何图形之间的关系，在脑海中初步形成立体的、形象的几何图形，促进初中生的几何直观意识形成.

如，在“立体图形与平面图形”的教学中，教师若是在黑板上划出几个立体图形、平面图形，然后进行特点的讲解以及区别的分析，则很难引起学生的关注，为了能够让学生自主地构建立体图形与平面图形的特征，引领学生在对图形的特征观察中树立几何直观意识，教师可以从生活中选择符合“立体图形”的实物，如模仿、足球、鞋盒、笔筒、漏斗，这些都是学生们日常生活中经常能够接触到的物体，以学生熟悉的几何体观察入手，让学生从实物的观察中发现立体图形，如长方体有6个面、12条棱，8个顶点，正方体属于特殊的长方体，因为其除了具备长方体的特征之外，每一条棱的长度均相等，对比平面图形则不具备这些特征.在实物观察之后，教师可以鼓励学生思考：“你还知道哪些生活中的立体图形？同学们在观察之后，是否能够尝试总结出立体图形的数学概念？”此时，有的学生说帐篷，有的学生说金字塔，还有的学生说音响，由此建立了立体图形与生活物体之间的关系，并引领学生从观察中抽象出数学概念，初步形成了对几何物体与几何图形的观察意识，为学生的几何直观能力培养做好了铺垫.

2.利用数形结合，发展几何直观能力

“数”与“形”是数学领域中的两个最基本研究对象，在初中数学的教学中教师应善于运用“数”与“形”之间的关系，采取“数”转化为“形”，“形”转化为“数”的方式，追求数形结合的效果.数形结合是一种重要的数学思想方法，在几何直观能力的培养中，教师应引领学生通过观察与分析，发现直观几何图形与抽象性的数学符号、数学文字语言存在的关系，从而学会灵活地运用“数”与“形”的转化，将复杂问题简单化，以促进初中生几何直观能力的提升，学会透过几何直观的观察与数形的灵活转化，明晰问题解决的思路.

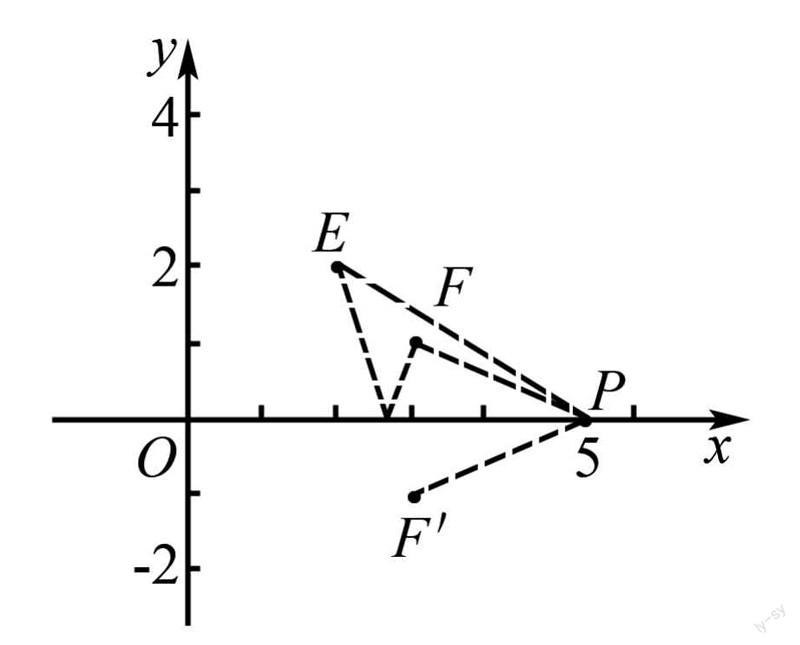
如，教师给学生们提出了这样一个问题：“求y=+的最小值”在此题的解答中大部分学生会采取代数法，但是运用代数法解决此类问题存在两个避免：第一是学生较难找到解题思路;第二是计算过程十分地繁琐，容易计算失误 .那么，教师则可以引导学生运用画图的方式輔助复杂计算题的解答，如下图所示，当学生划出辅助图之后，设点P（x，0），点F（3，1），点E（2，2），则很轻松地就可以推理出PE=，PF=，因此y=PE+PF的答案，那么学生们很快就找到了该题的解答思路，只要求出PE+PF的最小值，即为y的最小值.通过数字语言转化为图形语言的方式，帮助初中生建立了“数”与“形”的关系，将复杂的问题以更为直观的方式展示了出来，不仅可以促进初中生的几何直观能力发展，也让学生掌握了更为灵活的、便捷的解题技巧.

3.利用课件演示，拓展几何直观思维

初中生的知识阅历尚浅，在对数学图形的观察中学生所积累的知识无法满足各种各样的几何图形对认知的要求，针对这一问题，教师应采取有效的教学手段，帮助初中生在几何图形的观察中积累更多的表象知识，拓展学生的几何直观思维空间，以促进初中生的几何直观能力更高阶层发展.课件演示的普及及其在数学教学中的运用，帮助教师解决了教学中的难题，通过数学教学中播放动画、图片的形式，为初中生的几何图形学习创造出了生动有趣的情境，同时可以引领学生开拓直观思维，在观察之后进一步发散性地思考.

如在“三角形的三条角平分线相较于一点”的知识点讲解中，若是教师采取照本宣科的教学方法，指导学生通过“作图”、“观察”，进而得出结论，即使学生们通过先作图后观察的方法，最终得出了结论，也会存在这样的疑惑：“这个结论是不是个别现象”，学生无法从数学观察中总结出规律，发现数学本质.为了帮助学生深化对数学知识点的理解，拓展学生的几何直观思维空间，教师可以利用多媒体技术制作视频课件，通过课件播放的方式向学生直观地演示出三角形的三条角平分线交于一点，在拖动任意一个顶点时，三角形的形状就会发生变化，但是角平分线仍然相交于一点.通过动态的视频观察，可以帮助学生开拓思维空间，对已经积累的数学知識产生感性认知，再过渡到抽象思维的发展，为初中生的几何直观能力发展提供了助力.

综上所述可知，几何直观能力的培养是学生数学学习中必须要具备的能力，对于初中生的数学学习十分重要，为了更好地达到几何直观能力培养的目标，需要教师在数学教学中紧紧地围绕学科核心素养设计教学活动，遵循数学几何直观能力培养的原则，能够将几何直观能力的培养渗透于数学教学的全过程之中，通过生活实物展示、数形结合转化以及媒体课件展示等方式，提升初中生的几何直观思维，以助力初中生数学学习效果的提高.

参考文献：

[1]陈玉华.借助图形直观培养学生的几何直观能力[J].名师在线，2021（23）：10-11.

[2]陈碧月.培养几何直观能力发展数学核心素养的策略探究[J].考试周刊，2021（50）：75-76.

[3]郎颜潞.初中生几何直观能力现状调查研究[D].重庆：重庆三峡学院，2021.

[责任编辑：李 璟]