巧妙运用类比法 高效解答数学题

陈拾英

摘 要： 类比法是一种应用价值较高，综合性较强，灵活性较强的逻辑方法，它可以应用到各种情景中去.然而，就目前初中数学的现状而言，类比法失去了它原有的地位，只集中在比较基础的数学知识教学之中，为了提升学生的思想迁移能力，培养较强的思维能力，并且提高学习效率，我们更应该注重学习方法的教学，本文介绍类比法在初中数学解题中的灵活运用.

关键词： 类比法;初中数学;方法教学

中图分类号： G632       文献标识码： A       文章编号： 1008-0333（2021）35-0046-02

一、数与形的类比

数形结合是数学解题中的一个常见的解题方法，很多问题都需要学生在数和形之间不断进行转换才能得到最终解决，由此，老师们就经常忽视数和形的类比，反而以数形结合作为主要的教学方法和教学思路，导致学生们只会朝着一个方向走，一旦出现岔路口，就很容易失分，因此，老师们更应该注重数与形的类比应用教学.

例1  已知函数y= x2+1 + （8-x）2+25 ，试求出此函数的最小值.

解析  为了达到化繁为简，提高解题速度的目的，此题可以运用数形结合类比的方法，具体解题思路如下：

我们先观察这个函数，函数中有两个根号形式，这时我们可以想想哪个图形之中会出现根式，毫无疑问是三角形，因此，我们可以利用线段图形和三角形来对函数进行表示，如图1所示

根据已知的条件，利用类比法，我们可以将题目转化为：如图所示，点C就在线段BD上，已知BD=8，DE=5，并且BA⊥BD、DE⊥BD，连接线段AC、CE.

设BC=x，∴CD=8-x，

∴ x2+1 + （8-x）2+25 =AC+CE，

要求得此函數的最小值，所以当A、C、E三点共线时，（AC+CE）min=AE.

二、类似图形的类比

类比方法中有一种类比图形的方法，还有另一种说法叫做类似知识点的类比，虽然这类似知识点的综合性比较强，但是学生可以利用此知识点在短时间内找到问题的突破口，可以提高解题速度，还需要勤加训练，形成类似题型的快速解题思维.

例2  如图2所示，已知有正方形ABCD，点F在边BC上，点E为边AB上运动，并且DE⊥EF即∠ADE=90°.

（1）①请证明△ADE相似于△BEF;

②先假设AE=x，BF=y，已知AB=4，试求当ymax时，x为多少？

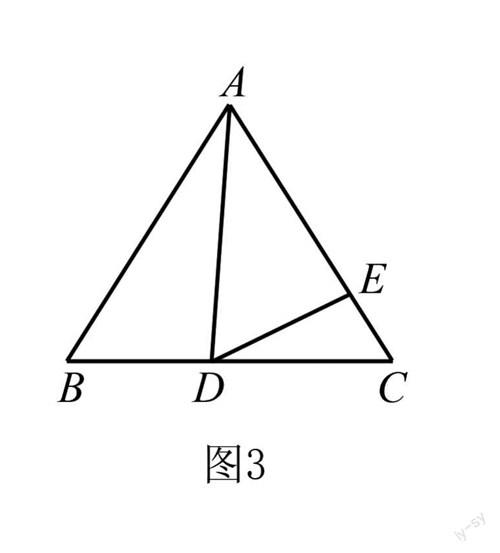
（2）如图3所示，已知有三角形ABC，点D在边BC上运动，点E在边AC上运动，AB=BC=AC=6，并且∠ADE=60°.

①先假设x=DC，y=AE，根据两个动点的运动以及两条边的关系，列出y与x的函数关系式;

②当△AED是等边三角形或者其他形状时，y有最小值.

解析  尽管两道小题的已知条件和题目给出的图形都不尽相同，但是解题思路有的相似之处，比如说，不管题目给出的图形是正方形还是三角形，它们有一个共同点，就是它们的底边都有一个运动的动点，并且动点与其他边所形成的三个角也都在底边上，遇到此类题目，我们就应该联想到证明相似三角形，证明相似之后，就可以使用相似三角形的知识点了，对应边与对应边成比例，这样就可以求出最后的答案了.

三、从简单到复杂的类比

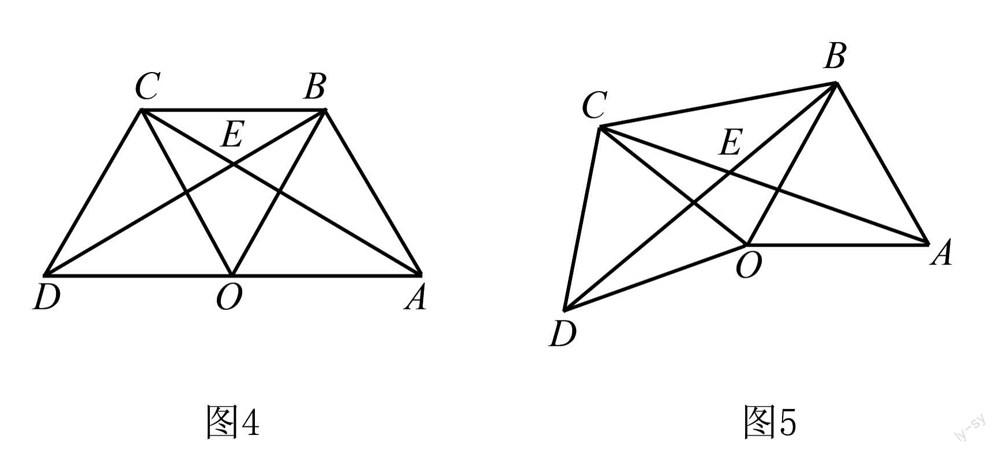
例3  如图4所示，在梯形ABCD中，存在△DOC和△OAB，并且这两个三角形均为等边三角形，已知点D、O、A三点共线，DO=OA，连接梯形对角线DB，且DB交AC与点E.

（1）请根据以上的条件求出∠AEB.

（2）如图5所示，和上一小题一样，△DOC、△OAB都是等边三角形，并且DO=OA，同样将DB连接起来，它交AC于点E，最后把BC连接起来，请根据已知条件求出∠AEB的度数.

例4  有一个三角形ABC，∠BAC=90°，并且AB=AC，BD=DC，BE=AF.

（1）如图6所示，如果点E在边AB上，点F在边AC上，请证明：△DEF是等腰直角三角形.

（2）如图7所示，倘若点E、F分别为线段AB、CA延长线上的一点，请根据已知条件证明△DEF为等腰直角三角形.

解析  对上述的题目分析，我们发现每一道题目的第一小问都差不多，并且难易程度也比较小.尽管已知条件不尽相同，且第二题的图形要比第一题的图形复杂很多，但是都是证明三角形全等，我们可以舍去那些没用的线段，使用相同的算法，如此，这便是类比教学方法的应用过程了.老师应该注重培养学生从不同角度出发看待问题，千万不能思维定式势，帮助学生理解题目隐藏的知识点，从而提高解题速度.

通过对上述三种不同类型的类比方法在数学题中的运用的解读，我们不难发现，对于一道数学题，可以有不同的解题思路和方法，然而类比法是一种逻辑性比较强的方法，它可以帮助学生们提高解题效率，培养思维迁移能力.因此，教师在教学过程中，不应该仅仅停留在浅层次的报答案，而应该找到更加适合学生的教学方法，从而做到教学相长.

参考文献：

[1]陈兆绪.类比中获新知应用中显能力——从初中数学类比法解题谈[J].数学教学通讯（中教版），2020（08）：68-70.

[2]沈宇华.初中数学类比法教学的运用和思考[J].数学教学通讯，2020（2）：69-70.

[责任编辑：李 璟]