复杂力学环境中完井管柱屈曲行为及其防控措施
2021-05-07练章华牟易升罗玉合
练章华, 王 天, 牟易升, 罗玉合, 张 潮, 高 旭
(1.西南石油大学油气藏地质及开发工程国家重点实验室, 成都 610500;2.中国石油西南油气田公司蜀南气矿, 泸州 646000;3.智慧石油投资有限公司, 克拉玛依 834000; 4.管道储运有限公司抢维修中心, 徐州 221008)
井下管柱是下井管柱及各种井下接头、工具、阀件的总称,是井下作业的主要承载和动力传递构件。作为一种特殊的机械构件,管柱在一定的应力水平下会发生变形;如果管柱的应力或变形过大,会导致管柱破坏、封隔器失效、控制头上移等作业事故。作业过程中管柱的屈曲既影响了其本身的受力与变形,又加大了井下作业的难度[1]。当油套管处于超深、超高温等复杂工况下时,管柱内的温度也随着产量增加而大幅增加,管柱将轴向伸长,油管柱底部封隔器的轴向压力也会增加,油管柱的屈曲变形将更严重。通过实际井况下完井管柱屈曲行为的研究与缓解措施的提出,对于完井管柱屈曲严重程度、影响因素的确定及提高油管柱使用寿命、防控措施的借鉴发展都有着重要意义。
早在20世纪50年代,中外学者就已经针对井下管柱的屈曲问题开展了大量的研究。Althouse等[2]首次采用能量法计算了钻柱失稳的临界载荷及钻柱发生屈曲后的弯矩。Han等[3]综合了有限单元法和影响系数法(ICM)构建影响因素矩阵的优点,考虑了残余应力和端部约束影响,分析了管柱的应力应变关系。Schwind[4]对井下管柱屈曲行为进行了研究并首次给出了正弦屈曲的临界载荷的求解方法。Allen等[5]深入探讨了带封隔器的多级管柱力学分析问题。Kyllingstad等[6]运用最小位能法分析了等曲率井中钻柱屈曲行为。Volk等[7]将该公式推广到了弯曲井眼的应用上,还结合了摩擦力等因素,推导出了因摩擦力而产生的螺旋屈曲载荷计算公式。高国华等[8]将管柱三种平衡方程统一起来分析了管柱在垂直井眼中的屈曲情况。Takach等[9]给出了钻柱螺旋屈曲的临界载荷表达式,并提出了一种新的常曲率井眼(如水平井建井段)屈曲模型。高德利等[10]在不考虑钻柱重力的情况下研究了封隔器对钻柱屈曲的影响。练章华等[11-12]根据水平井井眼轨迹数据及封隔器位置,利用有限元软件建立了完井管柱受力力学模型。Adnan等[13]通过假设连油屈曲形态的方法,利用能量法分析了残余应变力的连油屈曲。高立峰等[14]以套管-水泥环-地层为研究对象,建立套管柱有限元力学模型,推导并建立了位移函数、形函数的计算方程。Wilson[15]基于数值模拟方法得出了全井段3D接触力示意图。龚迪光等[16]分析了带封隔器的管柱受力数学模型,为油田管柱优选提供了理论指导。牟易升等[17]研究了扶正器对超深气井油管柱屈曲行为的影响。练章华等[18]建立了超深井全井筒油管柱屈曲行为分析的有限元力学模型并对油管柱屈曲形态进行了分析研究。Mou等[19]根据油田管柱失效统计数据,对高温高压超深井油管接头螺纹的疲劳,量化油管接头螺纹的疲劳寿命,进行了试验研究、弹塑性力学模拟和多轴疲劳计算。许杰等[20]基于管柱平衡微分方程,综合考虑接触力、摩阻力等因素,针对曹妃甸油田一口浅层大位移井,预测管柱作业极限,并提出优化设计方案。
以上学者的研究得到或发展了一些管柱屈曲方面的经典理论公式,对后人继续深入分析与新理论、新模型的应用都可以作为重要的理论依据,而研究复杂工况下的管柱受力情况,其根本目的与亟需解决的问题在于寻找系统而有效的缓解复杂工况下的管柱屈曲措施,前人尚未涉及此领域。基于以上情况,现通过采用有限元法来对上述问题进行研究与分析,系统地归纳出各影响因素对复杂工况下管柱屈曲问题的缓解力度并加以评判,分析并提出了减少产量、伸缩管设计、扶正器设计等能够最优化油管柱使用寿命的方法,为之后油管缓解措施的发展提供了参考价值。
1 管柱力学问题理论
完井管柱在射孔、挤酸、试采、生产等作业过程中,油管内压、外压、井筒流动参数以及井筒温度等均随作业情况和生产工况改变而改变,导致管柱的轴向载荷、弯矩、管柱与套管间支反力、井筒流动摩阻等载荷以及管柱的轴向变形也随作业和生产工况发生改变。超深高温高压气井作业和生产过程中,这种改变往往更加严峻,使得完井管柱轴向变形过大,进而导致封隔器失封,且过大的螺旋弯曲会使下部管柱失效。
温度效应、活塞效应、螺旋屈曲效应、鼓胀效应、摩阻效应[21-22]分别引起的完井管柱长度变化量为ΔL1、ΔL2、ΔL3、ΔL4和ΔLkf,这些基本效应理论即为引起油管柱-封隔器整体系统受力变形的各个因素。在作业和生产过程中,通过推演可推算出各因素导致的油管柱的轴向位移表达式[23],即
ΔLkf=ΔL-ΔL1-ΔL2-ΔL3-ΔL4
(1)
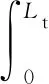
(2)
(3)
(4)
(5)
(6)
式中:ΔPi和ΔPo分别为封隔器坐封前后完井管柱内外的压力变化,MPa;ΔPi(s)为完井管柱s点处内压的变化值,MPa;ΔPo(s)为完井管柱s点处环空流体压力的变化值,MPa;Ln为第n级完井管柱的长度,m;Lt为从井底到s点处的完井管柱长度,m;Ain、Aon分别为第n级完井管柱内径和外径包围的面积,mm2;ΔFhsn为第n级管柱活塞力的变化值,N;Ap为封隔器密封腔截面积,mm;E为完井管柱的弹性模量,MPa;I为完井管柱横截面积对其直径的惯性矩;μ为泊松比;β为材料热膨胀系数,m/℃;Th(s)为当前工况下完井管柱s点处的温度,℃;Tqs为参考工况下完井管柱s点处的温度,℃;Ws为单位长度完井管柱在空气中的平均重量(包括接箍),N/m;Wi为单位长度完井管柱中的流体重量,N/m;Wo为单位长度完井管柱体积所排开套管中气体的重量,N/m;Ai、Ao分别为完井管柱内径和外径包围的面积,m2。
2 有限元理论
2.1 有限元力学模型建立
表1为X井油层套管数据表,该井完钻井深为5 828.00 m,完井方法为射孔完井,地层压力为92 MPa,油压为58 MPa。在投产前井口温度为24 ℃,地层温度为175 ℃。坐封时管外流体密度为1.0 g/cm3。生产时,油管底部轴向压力为295 kN,井口油压为55 MPa,井口温度为145 ℃,产量为200×104m3/d。
根据表1中油管柱的结构尺寸数据,建立了如图1所示的油管柱屈曲有限元力学模型与温度曲线。且对A、B两点进行了全固定约束。
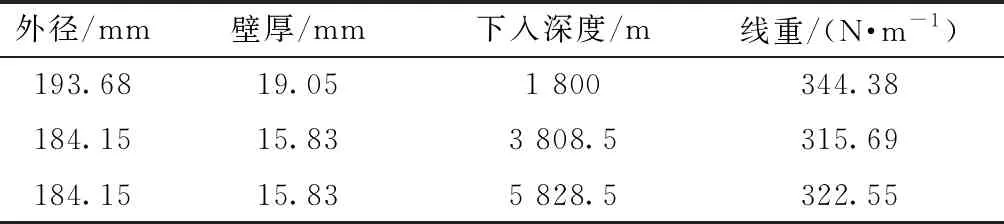
表1 油管柱参数表Table 1 Tubing string parameter table
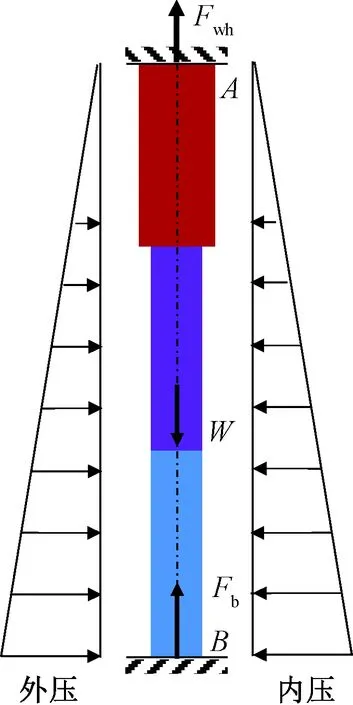
Fwh为井口提拉力,N;W为管柱质量,kg;Fb为底部轴向力,N图1 油管柱有限元力学模型Fig.1 Finite element mechanical model of tubing string
2.2 边界条件
图1中力学模型的边界条件包括:管柱自重W、内外流体压力、B点处的底部轴向压力Fb、油管柱整体外部所受静压力作用、管柱内部受井口油压等压力作用、A点处的提拉力Fwh以及温度变化引起的热应力。
采用PIPE288作为建立该油管柱力学模型的单元模型,该单元是三维中的线性、二次或三次双节点管道元素且基于梁理论和一阶剪切变形理论,在变形过程中管单元的横截面始终保持为平面,该单元可用于细长管或粗管,管的长细比可以用来判断单元的适用性,另外该单元还可提供附加质量、水动力附加质量和载荷以及浮力载荷。图2为最常用PIPE288单元的几何结构。
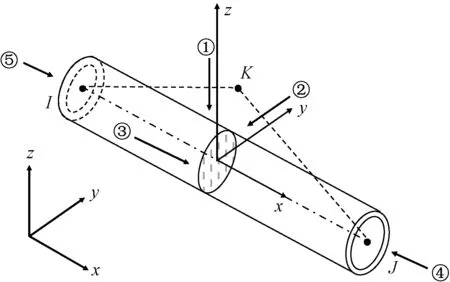
①和②为不同方向上的压力张量,MPa;③为单元内部摩阻力,MPa;④和⑤为单元管的轴向力,MPa;K为刚度;I、J为Ansys软件中梁单元的标记符号图2 PIPE288单元形状Fig.2 Shape of PIPE288 unit
3 有限元分析
油管柱的屈曲问题属于非线性的力学分析过程,只有当底部轴向载荷越过一临界值时,管柱才会发生屈曲变形,在油管柱生产过程中,为了保证油管柱的安全生产,需要尽量消除油管柱的屈曲形态,即寻求降低或消除油管柱底部的轴向压力,使其低于其临界屈曲失稳载荷。
图3为油管柱任意视角下屈曲位移图,在苛刻的工况下底部的油管柱发生了较为复杂的屈曲构型,整段屈曲段长达2 400 m,在屈曲段上靠近井口的部分位置呈现出了典型的正弦屈曲,靠近底部位置的油管柱发生了螺旋屈曲。在纯正弦屈曲段与纯螺旋屈曲段之间夹着一段不稳定的屈曲段,该段是正弦屈曲向螺旋屈曲的过渡段。此时,油管柱在X方向与Y方向上均与套管接触。
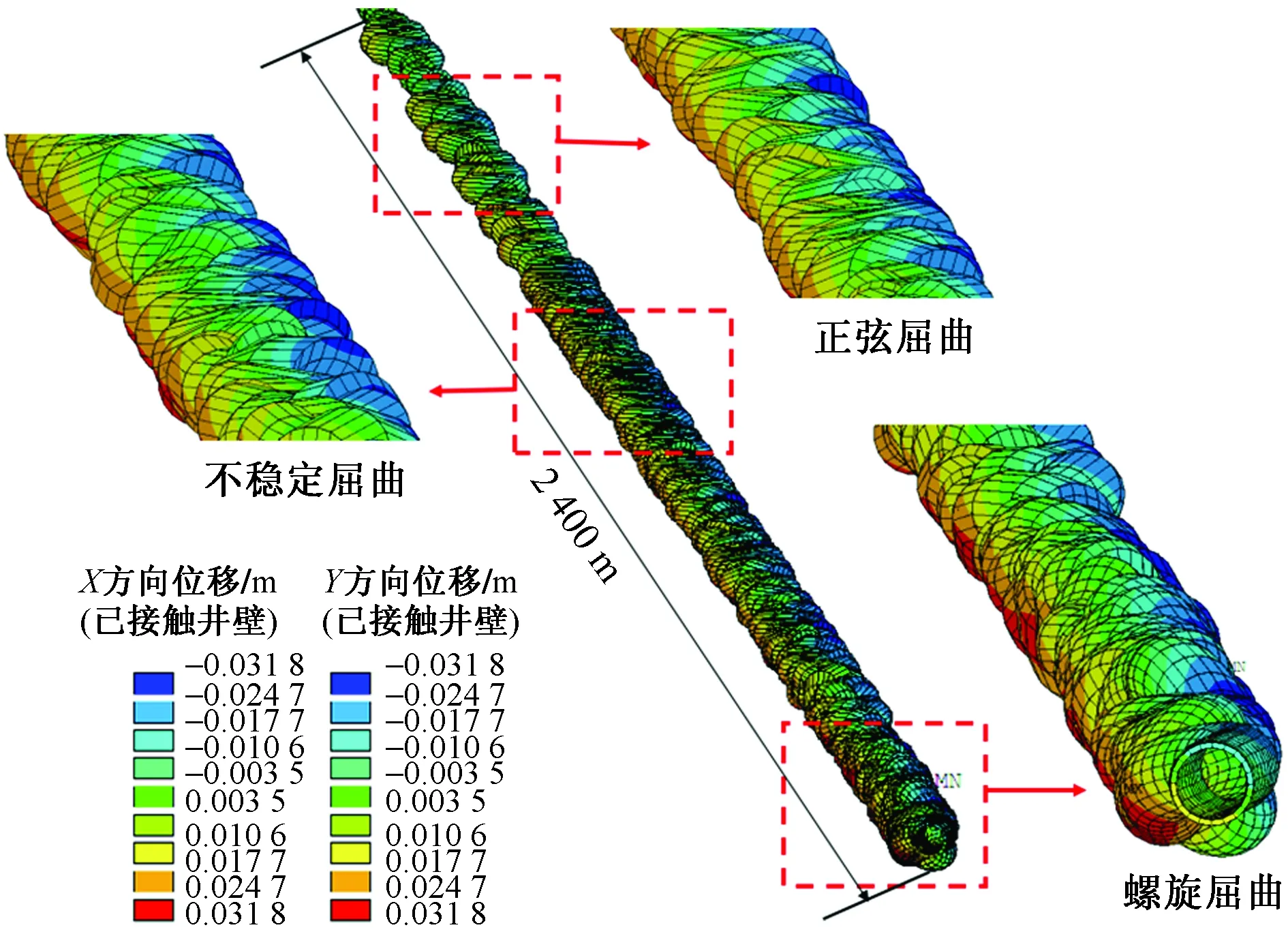
图3 超深高温高产气井管柱任意视角下屈曲形态Fig.3 Buckling shape of ultra deep high temperature and high yield gas well string from any angle
图4为实际井况下管柱屈曲形态的横向视图,可知,油管柱在X与Y方向均发生了较大的位移,X方向上的接触位置相比于Y方向较为密集且已经与井壁密切接触处较多,屈曲形态在所有屈曲段上的形态自上而下包括:正弦屈曲、不稳定屈曲段、螺旋屈曲段。分析可知,一旦发生屈曲,油管柱必然在X方向上发生位移,之后Y方向上的位移也随着轴向力的增大而逐渐增加,屈曲形态由纯正弦屈曲形态向螺旋屈曲形态过渡。
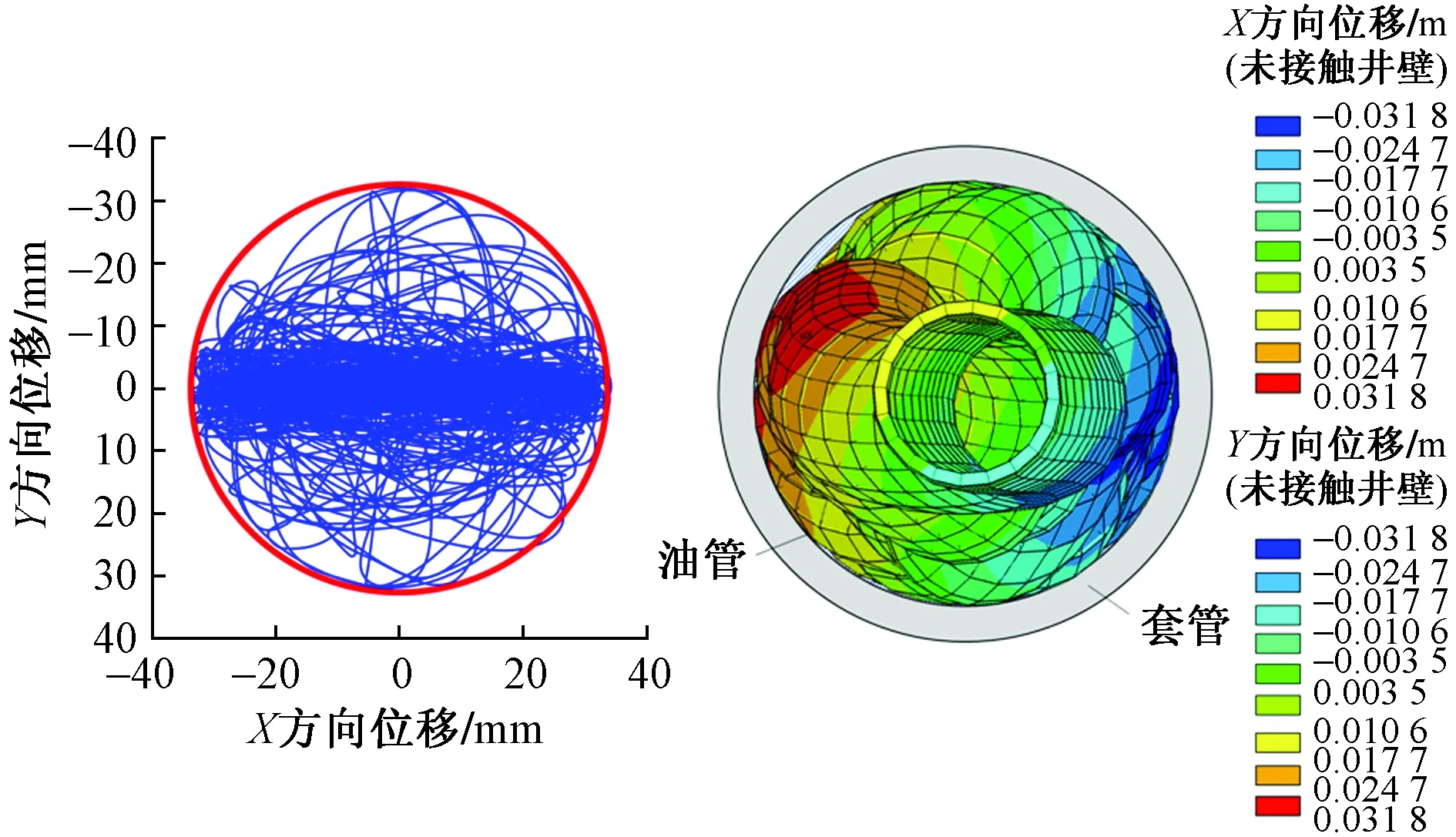
图4 超深高温高产气井管柱横向位移俯视图Fig.4 Top view of lateral displacement of string in ultra deep, high temperature and high production gas wel
图5为实际井况下管柱横向位移轴向投影图,可以看出,油管柱的全部屈曲段在X方向上均有较大的位移且大部分位置都已经与套管接触;距离井口较近的屈曲段中,油管与套管接触位置较少,油管柱在Y方向上位移较小且并未与套管接触;随着井深的增加,油套管位置在X方向上接触较多,同时油管柱在Y方向上的位移逐渐增加,随着井深超过5 500 m后,油管柱在Y方向上的位移已经与井筒接触,意味着从井深5 500~7 300 m井段的油管柱产生了螺旋屈曲的构型。

图5 超深高温高产气井管柱横向位移轴向投影图Fig.5 Axial projection of lateral displacement of string in ultra deep high temperature and high production gas well
4 防控措施
管柱的屈曲行为对石油工程中的钻井、完井、压裂及采油等方面都有着不良影响,严重时会引起钻头方向的改变以及井下摩阻和扭矩的显著增加致使管柱“锁死”,导致钻具疲劳破坏、油管密封失效以及管柱连接失效等。因此,针对加扶正器、优化产量以及伸缩管设计等措施对管柱屈曲的影响程度开展研究。
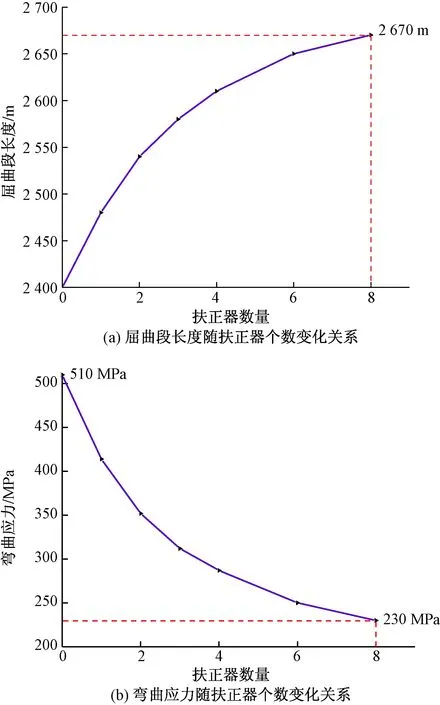
图6 全井段油管柱屈曲段长度和管柱弯曲应力随扶正器个数变化关系Fig.6 Relationship between length of buckling section and bending stress of tubing string with number of centralizers
图6为全井段油管柱屈曲段长度和管柱弯曲应力随扶正器个数变化关系曲线,可知,随着扶正器个数的增加管柱弯曲应力呈现非线性的递减趋势。屈曲段长度随扶正器个数的增加呈现非线性的递增趋势。带有扶正器管柱的屈曲基本得以缓解,管柱弯曲应力迅速减小,分析可知,从能量角度而言,由于底部轴向力对油管的做功,油管以屈曲的形式存储弯曲应变能,弯曲应变能与屈曲段长度成正比,由于扶正器的作用力使得油管横向位移减小,油管以增长屈曲段的形式来平衡弯曲应变能,因此加扶正器的油管横向位移小,而屈曲段变长。
图7为全井段油管柱屈曲段长度和管柱弯曲应力随伸缩短节数变化关系曲线,可知,随着伸缩短节数的增加屈曲段长度和管柱弯曲应力都呈现非线性的递减趋势。
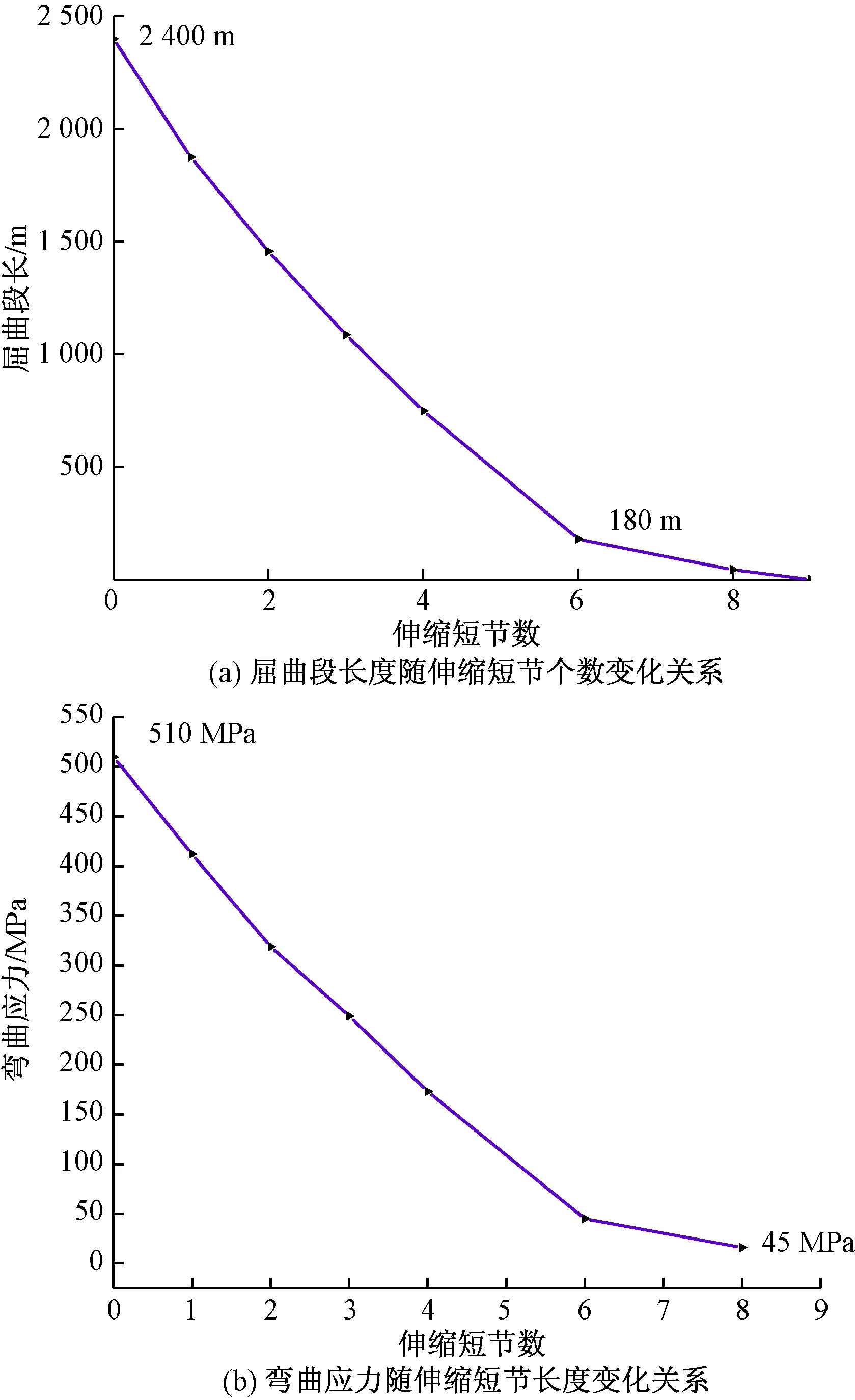
图7 全井段油管柱屈曲段长度和管柱弯曲应力随伸缩短节个数变化关系Fig.7 Relationship between length of buckling section and bending stress of tubing string with the number of expansion joints
在本文工况下,当伸缩短节数达到6个后,全井段油管柱的屈曲段长度和管柱弯曲应力的减小速率大幅降低,伸缩短节的个数影响大幅减弱。当伸缩短节数为9个后,全井段油管柱不发生任何屈曲构型。
图8为全井段油管柱屈曲段长度和管柱弯曲应力随产量变化关系曲线,可知,随着产量的增加屈曲段长度和管柱弯曲应力均呈现非线性的增加趋势。可以看出,产量对油管柱的屈曲程度影响较为明显。
在本文工况下,当产量从30×104m3/d增加到105×104m3/d时,屈曲段长度和管柱弯曲应力迅速上升,屈曲段长从85 m增加到了2 430 m,当产量超过105×104m3/d后屈曲段长度和管柱弯曲应力同样会有迅速增加的趋势,但增加速率有所减小。由于产量为30×104m3/d时,管柱的屈曲程度处在较低的水平,可见,降低产量能够有效缓解油管柱的屈曲程度。
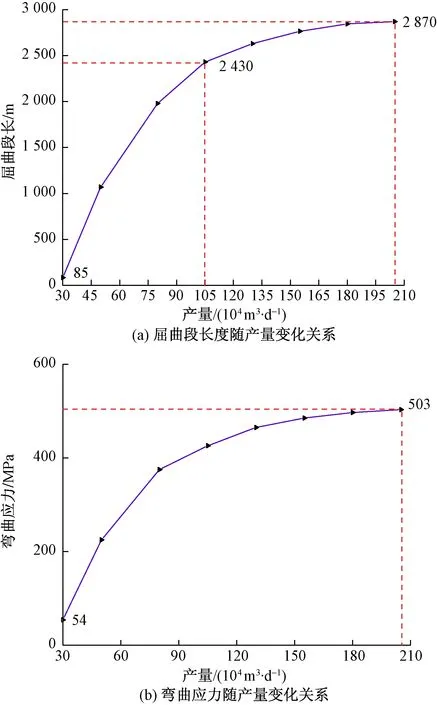
图8 全井段油管柱屈曲段长度和管柱弯曲应力随产量变化关系曲线Fig.8 Curve of length of buckling section of tubing string and bending stress of tubing string with production
5 结论
(1)实际井况下的油管柱发生了较为复杂的屈曲,屈曲段长达2 400 m,靠近井口的位置发生了正弦屈曲,靠近底部位置(井深超过5 500 m后)发生了螺旋屈曲,中间夹杂有不稳定的屈曲段。
(2)加扶正器会时油-套管最大弯曲应力有明显下降趋势,扶正器的作用力会使得油管横向位移减小,油管以增长屈曲段的形式来平衡弯曲应变能,因此加扶正器的油管横向位移小,屈曲段长。
(3)本文工况下,伸缩短节数达到6个后,全井段油管柱的屈曲段长度和管柱弯曲应力的减小速率大幅降低,伸缩短节的长度影响大幅减弱。当伸缩短节数达到9个后,全井段油管柱不发生任何屈曲构型。
(4)分析了加扶正器、优化产量以及伸缩管设计等措施对管柱屈曲的影响发现这些措施都可以起到缓解管柱屈曲的作用,对于本文所提到的实际工况而言降低产量与伸缩管设计对管柱屈曲中的扭矩改善最为明显,其次为扶正器设计。
