高能管系中管段长度比与最大热应力的关系

贺亚太 李余德，1) 武智愚 钱 公 郝瑞强 辛长春 张志明

*(上海交通大学船舶海洋与建筑工程学院，上海 200240)

†(大唐国际发电股份有限公司，北京 100033)

**(中国特种设备检测研究院，北京 100029)

††(中铝山西新材料有限公司，山西河津 043300)

***(山西国峰煤电有限责任公司，山西汾阳 032200)

†††(上海电气风电集团股份有限公司，上海 200233)

高温管道作为高温高压介质的输送工具，是火力发电、核电、化工及有色金属等行业不可或缺的关键部件。随着工业的发展和对热效率的追求，机组容量越来越大，运行参数越来越高[1-2]，管道的运行工况越来越严酷，对所用材料的要求也越来苛刻[3]。为此，与高温高压管道相关的研究也更加深入。

随着工业的发展，机组运行的温度和压强日益增高，管道运行的安全性显得尤为重要。管道是否能够安全运行是由设计、制造和运行维护共同决定的，因此首先需要设计理论的完善。设计的依据实际上是对管系应力分布的充分了解。早在100 多年前，文献[4-7] 中就研究过管道关键部位的应力分布，比如对于弯管在内压作用下的应力分布。经过100 多年的探索，仍然很难研究清楚。这些研究获得了计及弯管的柔度因子，即所谓的Karman–Hovgaard 因子：k= 1.65/h，其中h=tR/r2，与弯管的壁厚t，半径r和弯管中心线的曲率半径R有关。这些研究未完全搞清楚弯管的应力分布，因为弯管的实际应力分布受到来自管道系统载荷的影响，它随着管系的不同而变化，因此实际上不可能在理论上完全进行求解。

对于传输高温介质的管道，稳态运行时工作环境比较单一，因此实际上更主要的是关注管道材质的老化与损伤：蠕变过程。研究发现直管的蠕变仅产生在环向，长度方向不发生蠕变。弯管的蠕变首先以截面的复圆的形式发生[8]，直管的蠕变通过研究已经可以很好地进行预测[9]。

设计方面，采用材料力学的基本原理将管道视为无限长的空心圆筒体，取三个主应力中最大的环向应力作为设计壁厚的依据。实际上，设计受到运行参数的制约。按照运行温度选择材料，由于运行温度和压力决定了介质的密度，进而根据允许的流动速度选择管道的内径，最终结合材料的强度指标给出许用壁厚[10]。从这个过程来看，管道的环向应力只因设计参数而定，不受管系的热应力影响。换句话说，管道设计优劣的衡量标准之一是设计人员是否将管道的轴向热应力均匀设计。前面已经指出，许多力学家进行过管道一些关键部件的应力分析，但这些几乎均是考虑一个弯管的局部分析[4-5]。随着工业生产的发展，管道尺寸也在增加，弯管的数量不可避免地随之增加。对于整条管系的分析则以柔度分析为主[10-13]。

实际上根据设计人员的设计过程和应力分量的决定因素，可以知道，环向应力由运行参数决定，而且通常情况下(在轴向应力附加应力小于等于环向应力的1/2 时) 环向应力使管道发生蠕变损伤；由于管道是轴对称的，且可以自由膨胀，环向应力在稳态运行过程中不受温度的影响；管道作为薄壁管件对待，径向应力也主要由设计参数而定，所以起停温度变化主要影响管道的轴向应力。管道自身与保温材料和内部介质的重力由管道的支吊架系统承担。所以为了简化问题，本文突出管段长度和热应力的关系，不计重力的影响，也不考虑支吊系统的约束。通过审核不同设计院的50 多个电厂的管系图纸和支吊架检验调整工作发现：出现严重支吊架损坏的情况往往伴随着两相邻管段的长度悬殊很大的现象。特别是对一些存在显著安全隐患的管道进行改进之后[13]，笔者认为探索管段长度和位置排布对管系应力的影响在管道设计中具有重要的意义。

本文采用国际通用的简化模型方法，即将管道模型简化为空心圆管，提出相邻管段长度比的概念，采用柔度法计算管系热应力，用Matlab 软件计算处理，主要分析Hovgaard 管系、空间四管管系、空间五管管系乃至空间多管管系中管系相邻管段长度比和最大热应力的关系，并以此来探索空间管系结构允许的最短管段长度和最大管段长度比，得出一些对实际的管道设计有价值的参数。

1 模型

1.1 几何模型

本文研究平面L 型管系元素、Hovgaard 双弯管以及空间n管管系元素，模型如图1 所示。

图1 管系元素模型

对于更多管段的空间n管管系，其管段排布规则为在Hovgaard 管系的基础上，依次沿着管段L1，L2，L3的方向增加管段。

管道钢材料看做理想弹性且各向同性，将管道简化为空心圆杆。

1.2 力学条件

不考虑管系自重，且管系不受外载荷作用。将温度变化引起的热变形看作为等效载荷，两端固定，中间没有任何约束，用柔度法求解。

2 求解过程

2.1 L 型管系元素

L 型管系元素模型如图2，管系端点1 和2 为固定端约束。在固定端约束下，定义端点2 的位移D(分别为在X和Y方向的位移和绕Z的转动) 为

释放图2 中“2” 处的固定端约束，得到放松结构图3(a)，将固定端约束解除后代之以复原力，得到相当系统图3(b)。

此时，L 型管系元素图2 的两端固定的结构转变为图3(b) 中一端固定，另一端受未知约束力作用的结构。复原力R为

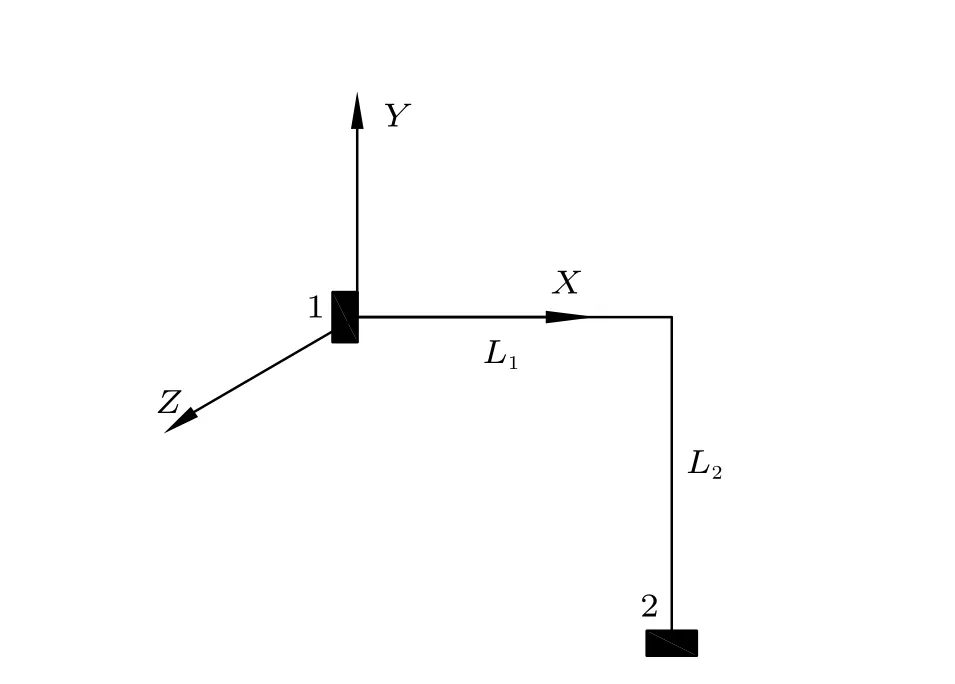
图2 L 型管系元素

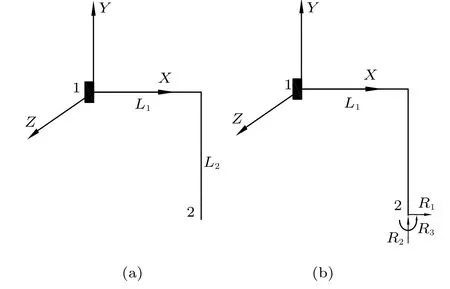
图3 放松结构和相当系统

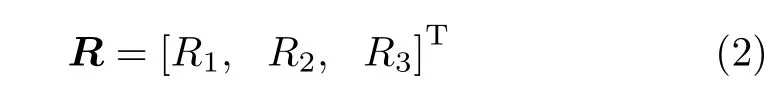
式中R1，R2，R3分别为端点2 处沿着X，Y方向的复原力和沿着Z方向的复原弯矩。

管系温度变化引起的热应变等效为外载荷。放松结构图3(a) 在等效载荷下产生变形(2→2′) (图4(a))，在复原力作用下产生变形(2→2′′)(图4(b))。

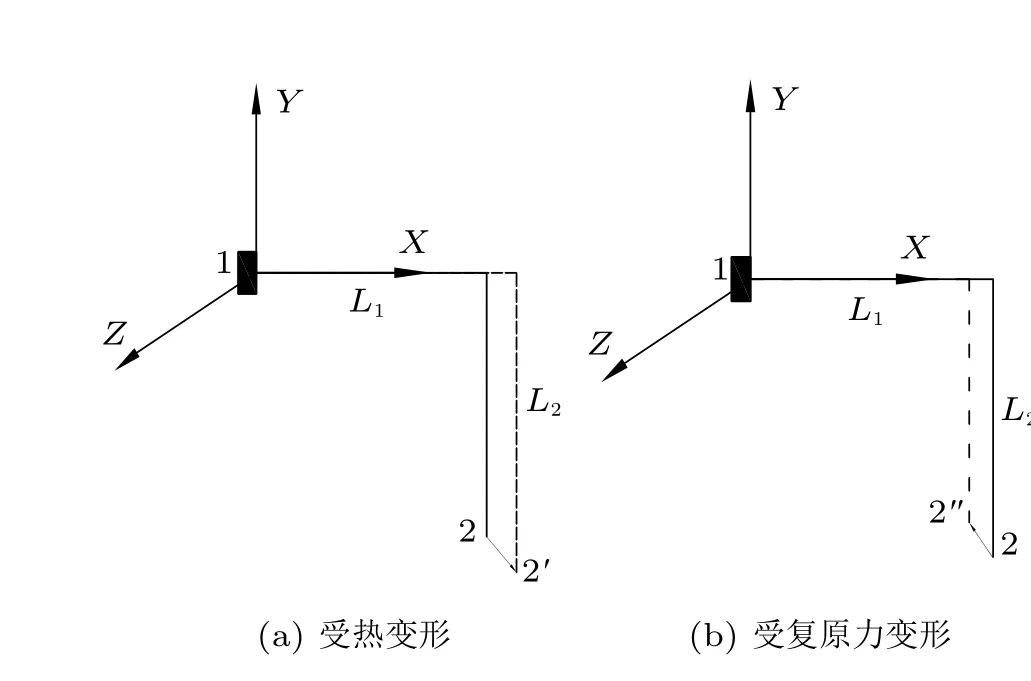
图4 结构变形

考虑到放松结构图3(a) 受等效热载荷时，端点2 为自由端，结合热效应，放松结构端点2 处受热变形为Dp，定义

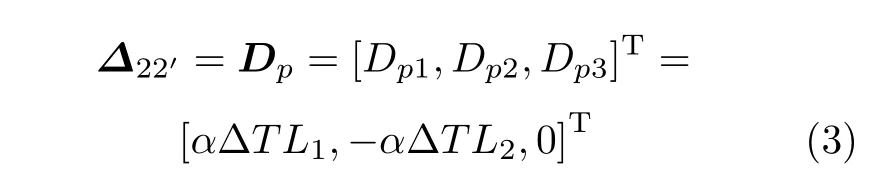
式中，Dp1，Dp2，Dp3为端点2 沿着X，Y方向的位移以及绕Z轴的转动分量。放松结构在复原力作用下端点2 变形至2′′，端点2 受复原力变形为DR，定义

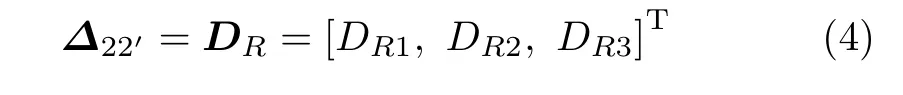
式中，DR1，DR2，DR3为端点2 沿着X，Y方向的位移以及沿着Z轴的转动。

由协调条件可知

为求DR，定义柔度矩阵

式中，柔度矩阵的元素Fij定义为：复原力Rj= 1作用在图3(a)的放松结构时，在端点2 处相应于Ri方向产生的位移(转角)，例如F21(图5)。那么，复原力Rj作用在图3(a) 的放松结构时，在端点2 处相应于Ri方向产生的位移为Fij ·Rj。

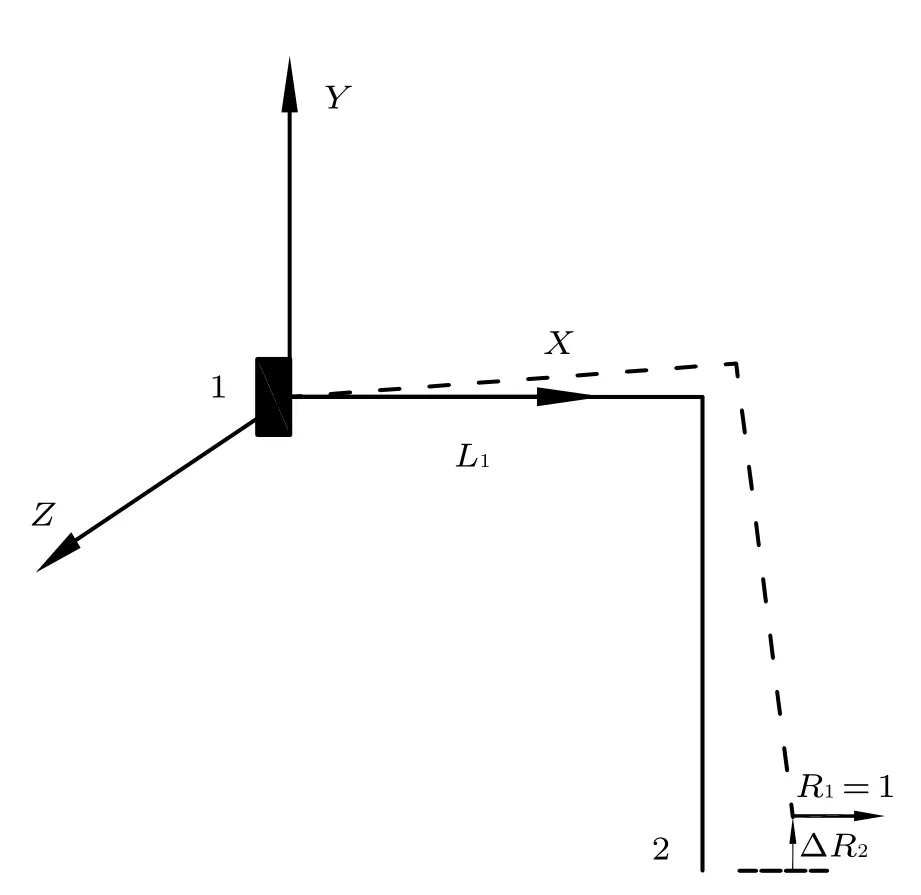
图5 柔度矩阵元素F21 物理意义图示

根据以上分析，F11，F12，F13分别为复原力R1= 1，R2= 1，R3= 1 在端点2 处相应于R1方向产生的位移。根据式(7)，复原力R1，R2，R3作用在图3(a) 的放松结构时，在端点2 处相应于R1方向产生的合位移为

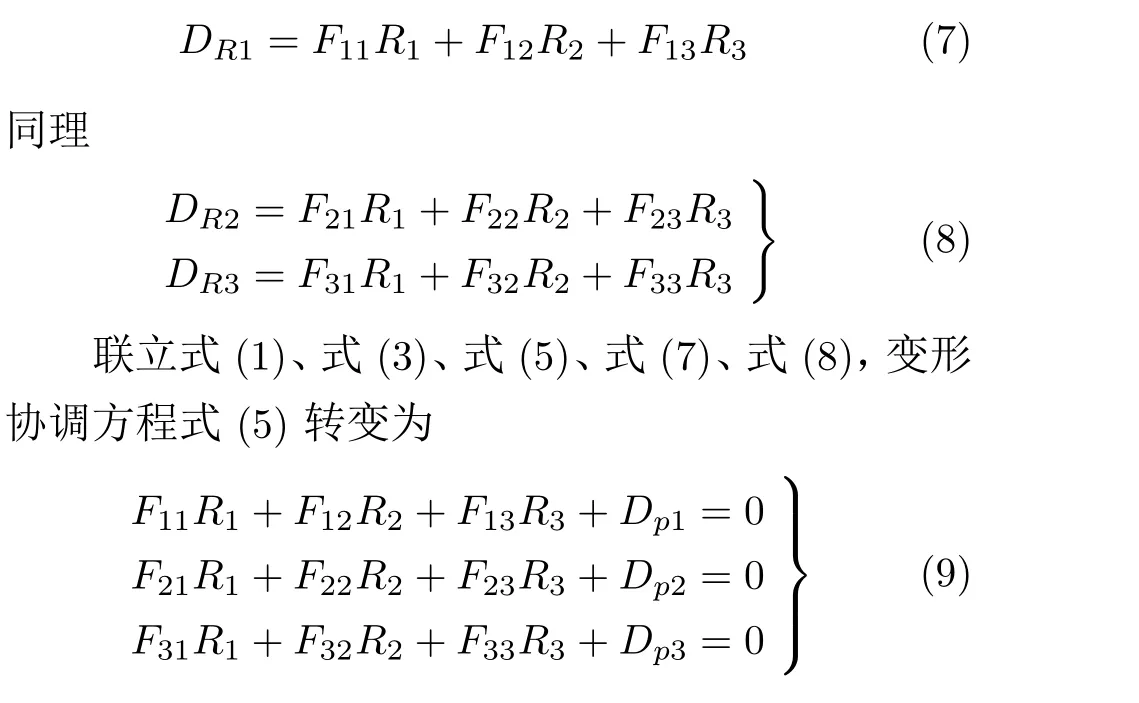
矩阵形式表达为

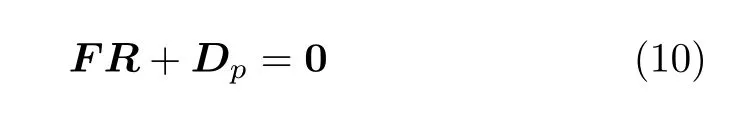
将式(10) 变形，有

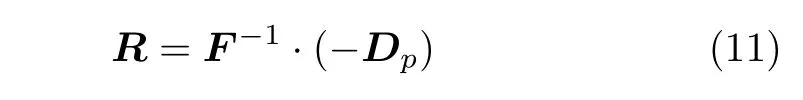
式中，Dp已经通过式(3) 求得，所以只要求出管系的柔度矩阵，就能求得管端2 处的复原力R，再由平衡方程即可求得管系全场的力、力矩和应力。

柔度矩阵由单位载荷法求解。将R1=1 看作在管系结构上作用于端点2 处的外载荷，根据单位载荷法，若要求结构在端点2 处沿着R2方向的位移F21，可在端点2 处假想一个沿着R2方向的单位载荷R2=1，由式(12) 求得

式中，ML表示结构外载荷(求解F21时即R1= 1)在结构上产生的弯矩，MU表示在结构待求位移点处作用的单位载荷(求解F21时即R2= 1) 在结构上产生的弯矩。MRi=1表示Ri=1 作用于端点2 处在管系上产生的弯矩。根据式(12)，运用图乘法，求解F21，得

将式(14) 的柔度矩阵代入式(11)，可以求得管系端点2 处的复原力R，将R代入图6，即复原力R在管系上引起弯矩。

图6 MRi=1 弯矩图

结合图7，运用叠加原理，可得平面两管L1，L2上的弯矩为

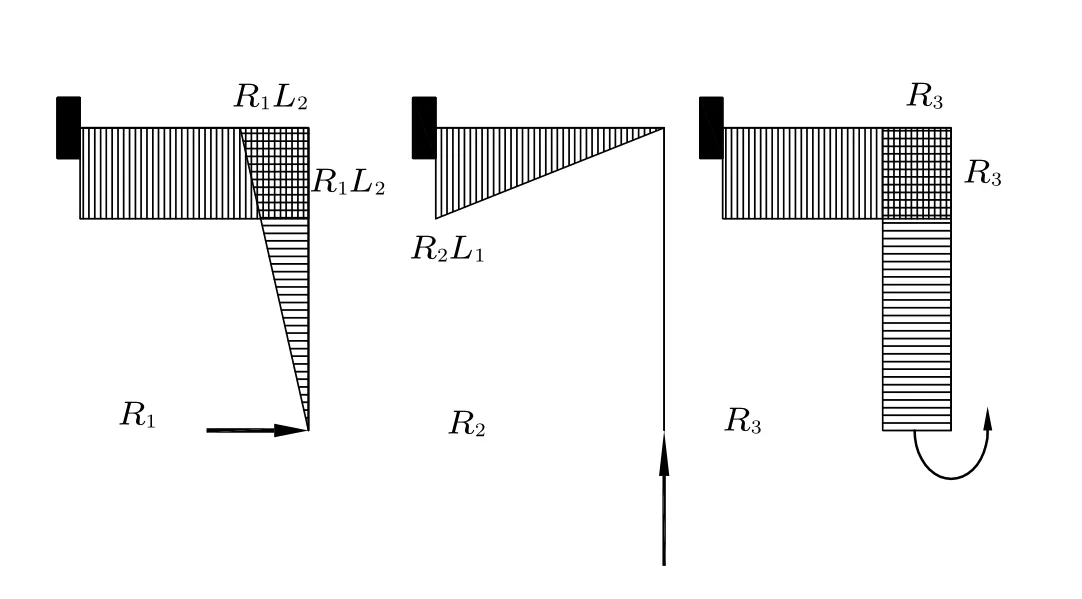
图7 MRi 弯矩图

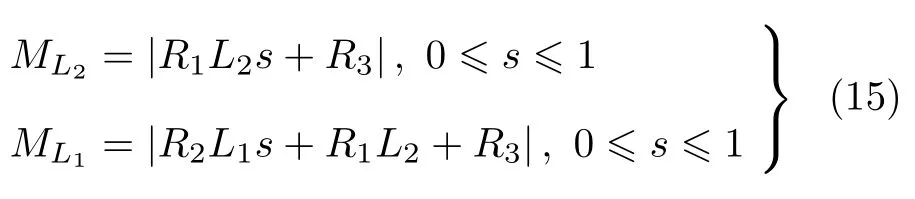
式中，参数s表征管段上不同位置，s从0 变化至1即管段位置从一端变化至另一端。通过式(15) 可以求得管段L1，L2上的各点的弯矩，而σ=M/W=Mr/I，如此便可求得杆系任一点上的热应力。

2.2 Hovgaard 双弯管管系元素

Hovgaard 双弯管模型如图 1(d)，与 L 型管系元素遵循同样的坐标系规则，其求解过程与 L型管系元素几乎一致，而与平面管系元素不同的是，Hovgaard 双弯管是空间管系，需要考虑扭矩。

求解Hovgaard 双弯管复原力的方程为

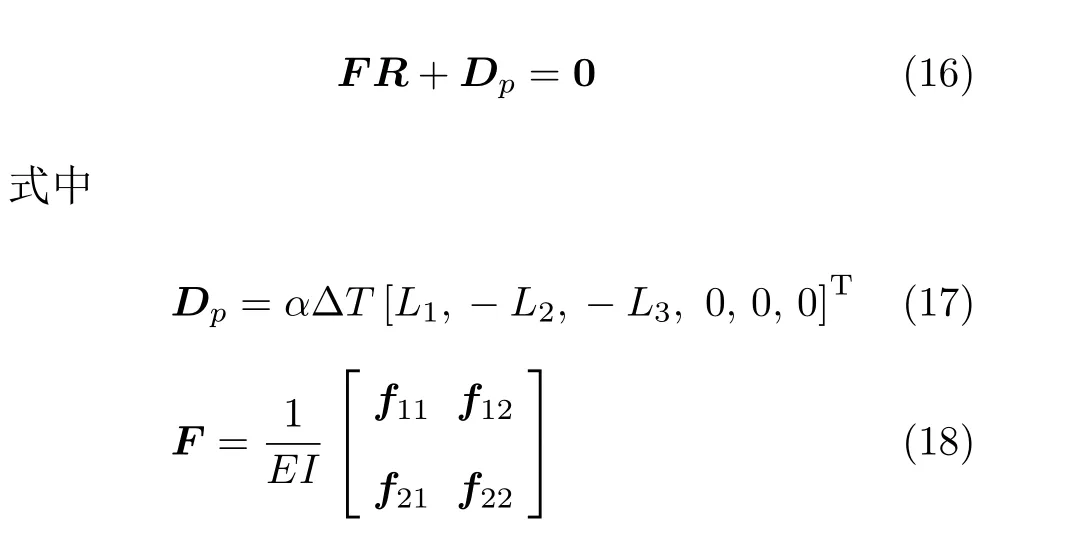
其中

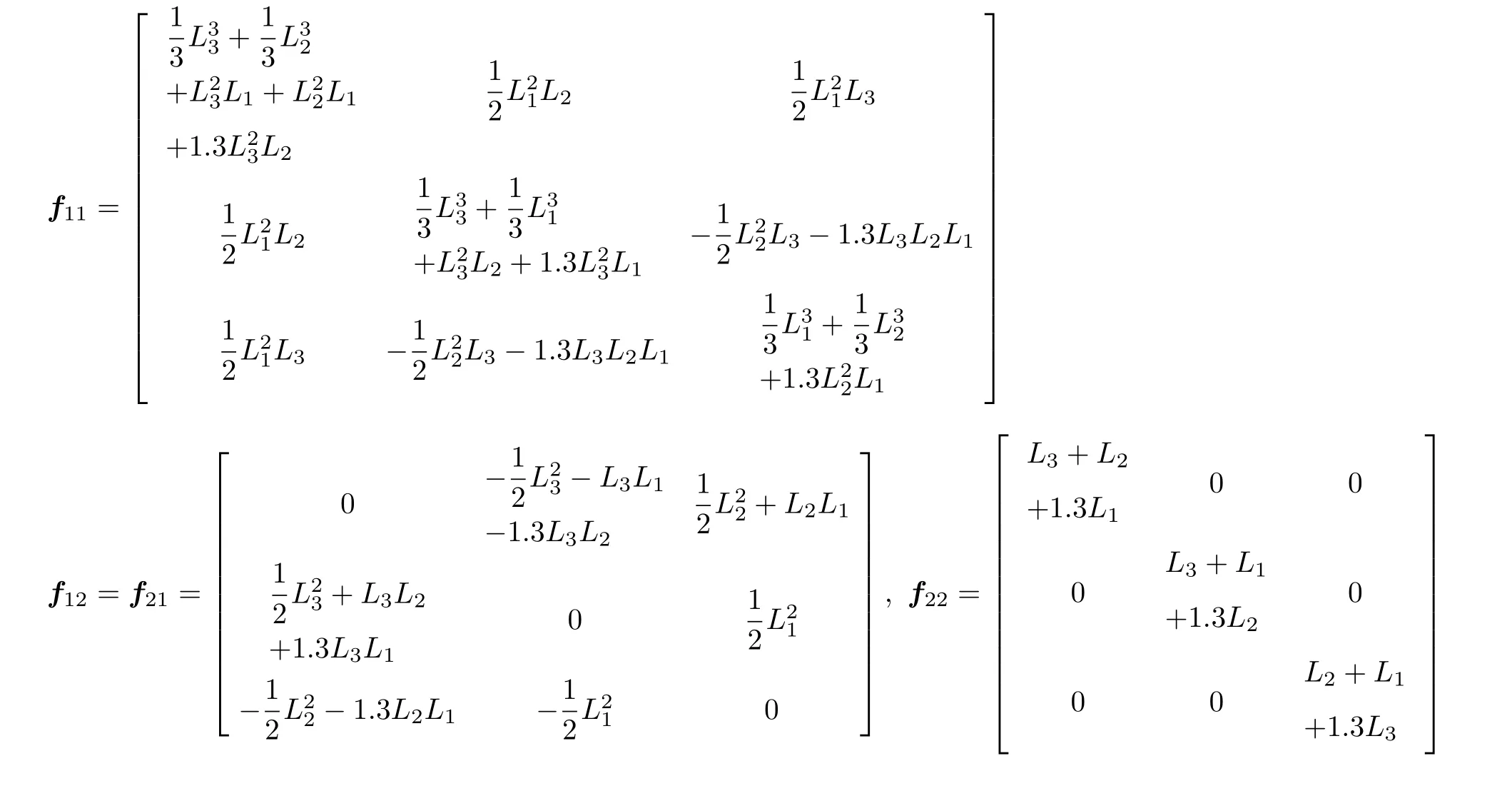
根据式(16) 求得复原力后，可以得出双弯管各管段的弯矩为(得出弯矩后，可以根据公式σ=M/W=Mr/I，求出各管段上各点的热应力)

2.3 空间四管管系元素

空间四管管系元素模型如图1(c)，与L 型管系元素遵循同样的坐标系规则，其求解过程与Hovgaard双弯管模型一致。求解复原力的方程为

式中

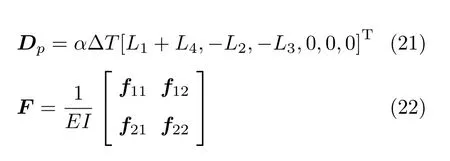
其中

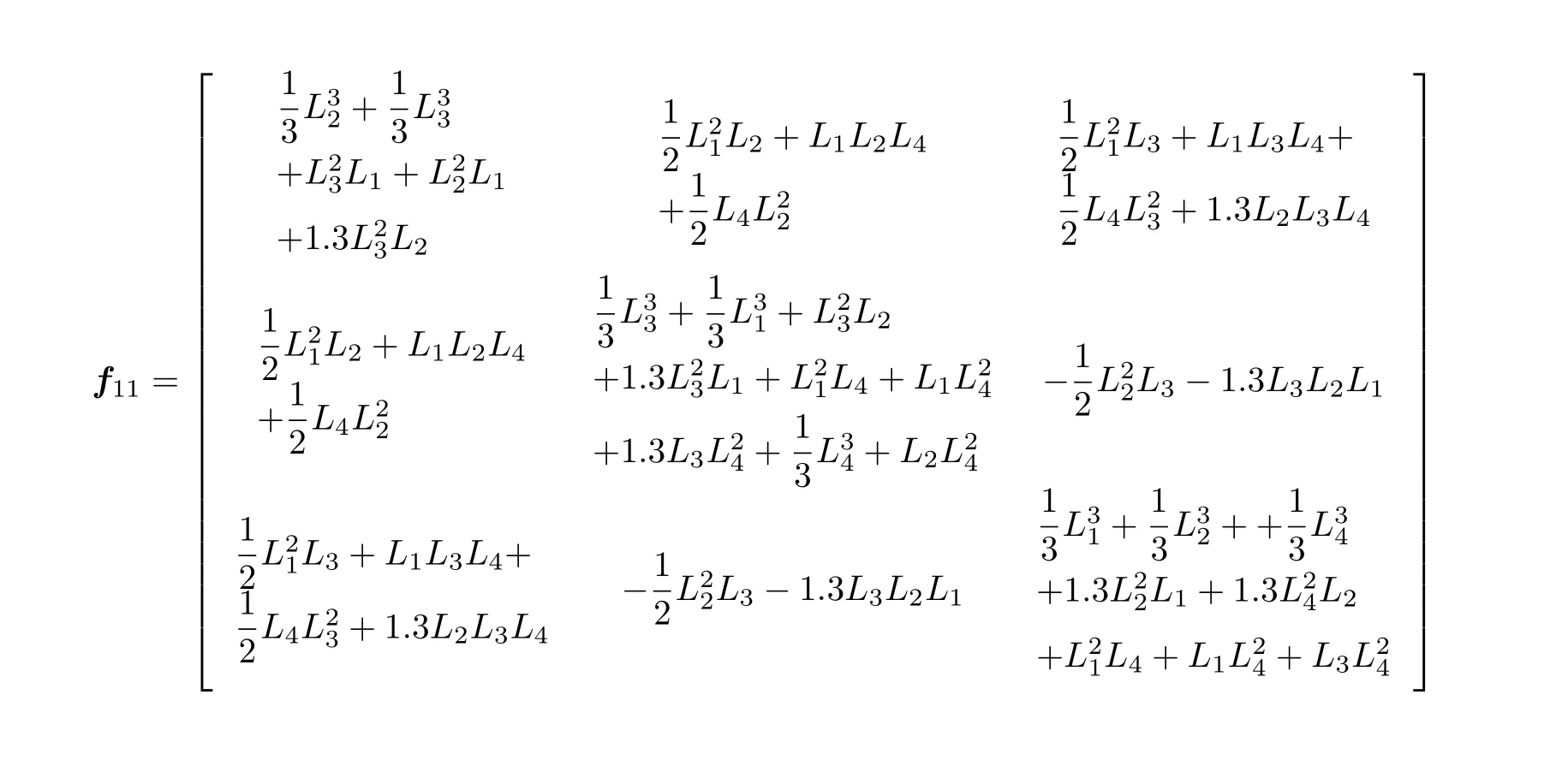
根据式(20) 求得复原力后，可以得出双弯管各管段的弯矩如下(得出弯矩后，可以根据公式σ=M/W=Mr/I，求出各管段上各点的热应力)

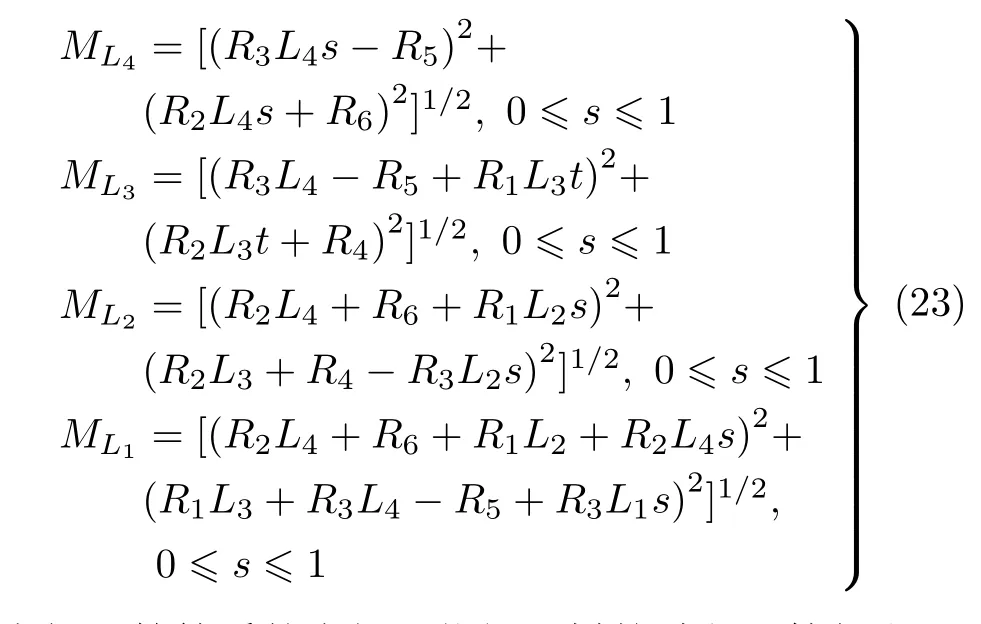
空间五管管系的求解可依据同样的过程计算得出。

3 结果

研究旨在探究Hovgaard 双弯管管系元素、空间四管管系元素以及空间五管管系元素中，管系的管段排布对管系最大热应力的影响。

为了更加方便地表征管系各管段的排布，引入参数RLi和RL

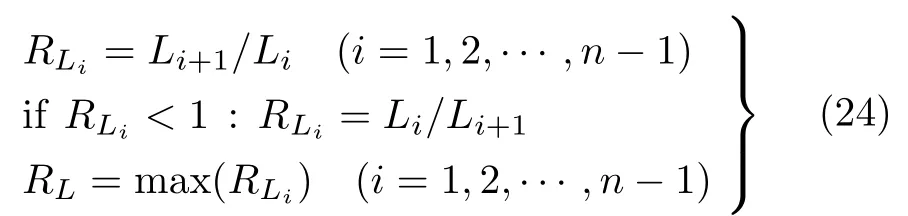
其中n为管系管段数，RLi表示相邻管段Li与Li+1长度的比值。在分析过程中为了方便比较，我们设定RLi不小于1，即总是大的值比小的值。RL为RLi中的最大值，代表管系相邻管段长度的最大差异。将RL称为管系相邻管段长度比，作为表征管系管段长度分布均匀性的参数，RL越接近1， 管系各管段长度分布越均匀。

其中σLi为管段Li上各点的热应力值，σi为管段Li上的最大热应力值，σlmax表示某种排布方式下管系上的最大热应力，作为表征管系最大热应力的参数，σgmax表示管段长度比相同的所有排布方式中最大的热应力，表征管系在此管段长度比RL下可能出现的最大热应力值。

结合管系材料的参数和允许的应力范围(许用应力、屈服应力等)，可以得出管系允许的最短管长，同时，在最短管长度确定的前提下，可以得出管系允许的最大相邻管段长度比。

以流程图展示研究过程如图8 所示，其中，Li′表示管系管段的变化梯度，由长度La变化到长度Lb，变化梯度为ΔL，Li表示由Li′缩放而来的实际研究过程中各管段的长度。

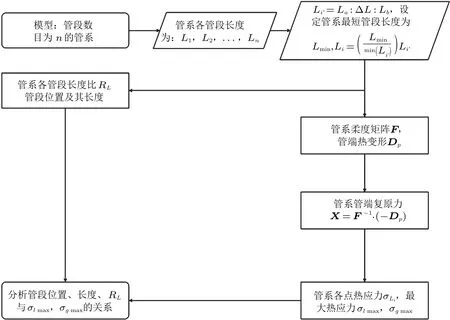
图8

根据图 8，在 Matlab 中进行循环计算，得出结果后即可分析RL与σlmax，σgmax之间的关系。

3.1 管系相邻管段长度比对最大热应力的影响

将管系中最短的管段记为Lmin，讨论空间管系各管段的排布对管系最大热应力大小的影响。经过Matlab 计算，得出图9 的变化趋势。图中横坐标为管系相邻管段长度比RL，纵坐标为同管段长度比相同的各种排布方式中管系的最大热应力σgmax=αΔTER/Lmin。

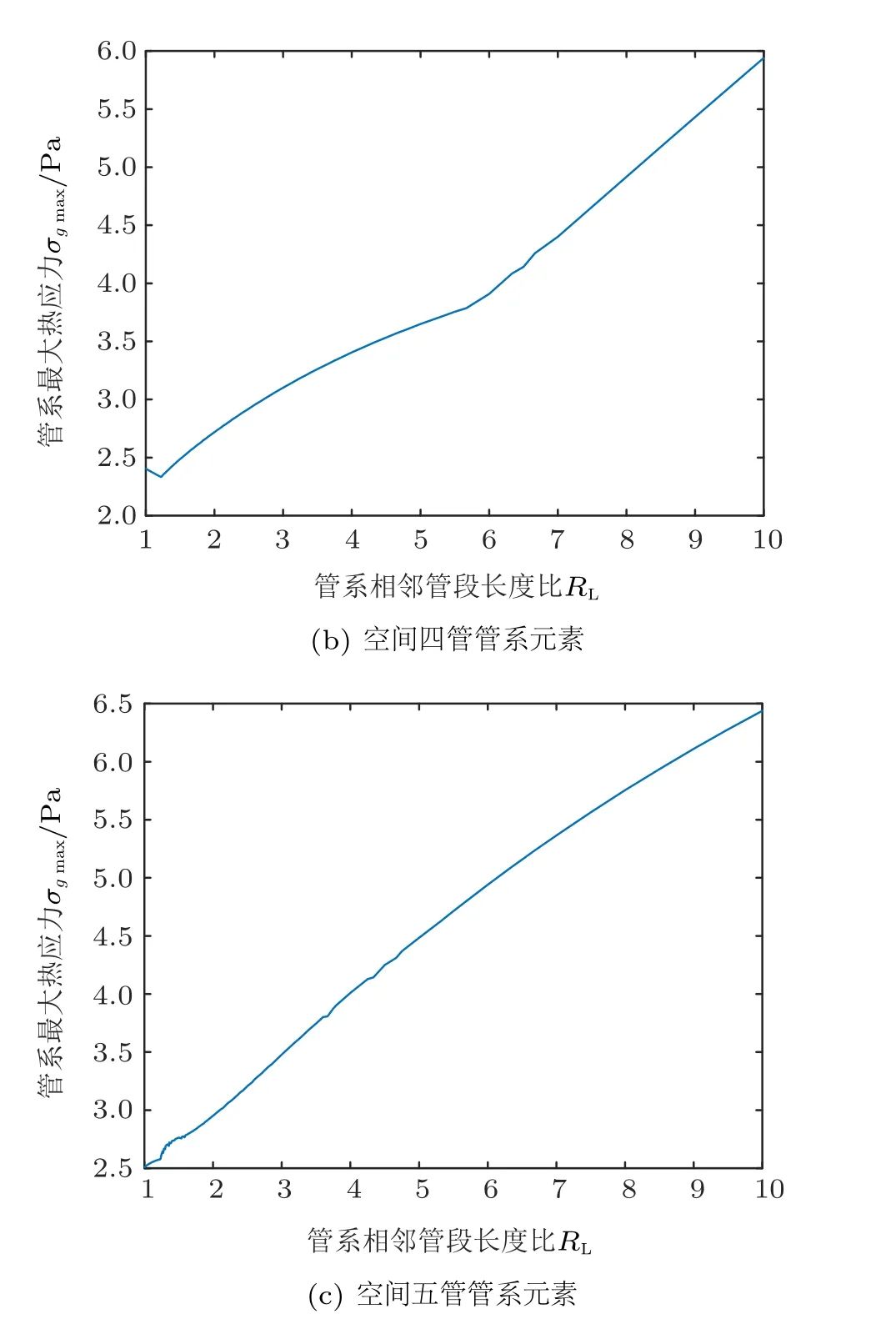
图9 管系相邻管段长度比与最大热应力的关系

由图9 可以看出，若管系最短管段长度是一个确定值，管系管段长度比越大，同长度比下各种排布方式中最大的热应力也会越大，且近似呈线性关系，且当管系的相邻管段长度比RL趋近1 时，管系的最大热应力最小。

3.2 管系允许的最短管长

由图9 可以看出，管系在同管段长度比RL下可能出现的最大热应力σgmax与管系的最短管长有关。当管系最短管长确定时，即RL趋近1 时，管系最大热应力最小。所以，选取管系管段等长排布即RL= 1 时的情况，来求解管系允许的最短管长，即若管系的最短管长超过此长度，那么即使管系以最佳的方式排布管段(即RL= 1) 也不能使管系的最大热应力满足许用应力/屈服应力的条件。

以 A335P91 钢材为例， 管道外径D=333.05 mm，管壁厚t= 30 mm，弹性模量E=154.7 GPa，膨胀系数α=13.009×10-6K-1，管道的工作温度由20°C 变化到546°C，工作温度下的许用应力[σ]=95.82 MPa，材料屈服应力σs=205 MPa。

经过Matlab 计算，得出图10 的变化趋势。图中横坐标为空间管系管段等长排布时管段的长度，纵坐标为相应情况下的最大热应力σgmax(RL= 1 时只有一种管系排布方式，此时，σlmax=σgmax)。图中点的横坐标为管系最大热应力等于管系材料(A335P91钢材) 的许用应力/屈服应力时的管系管段长度，纵坐标为许用应力/屈服应力。

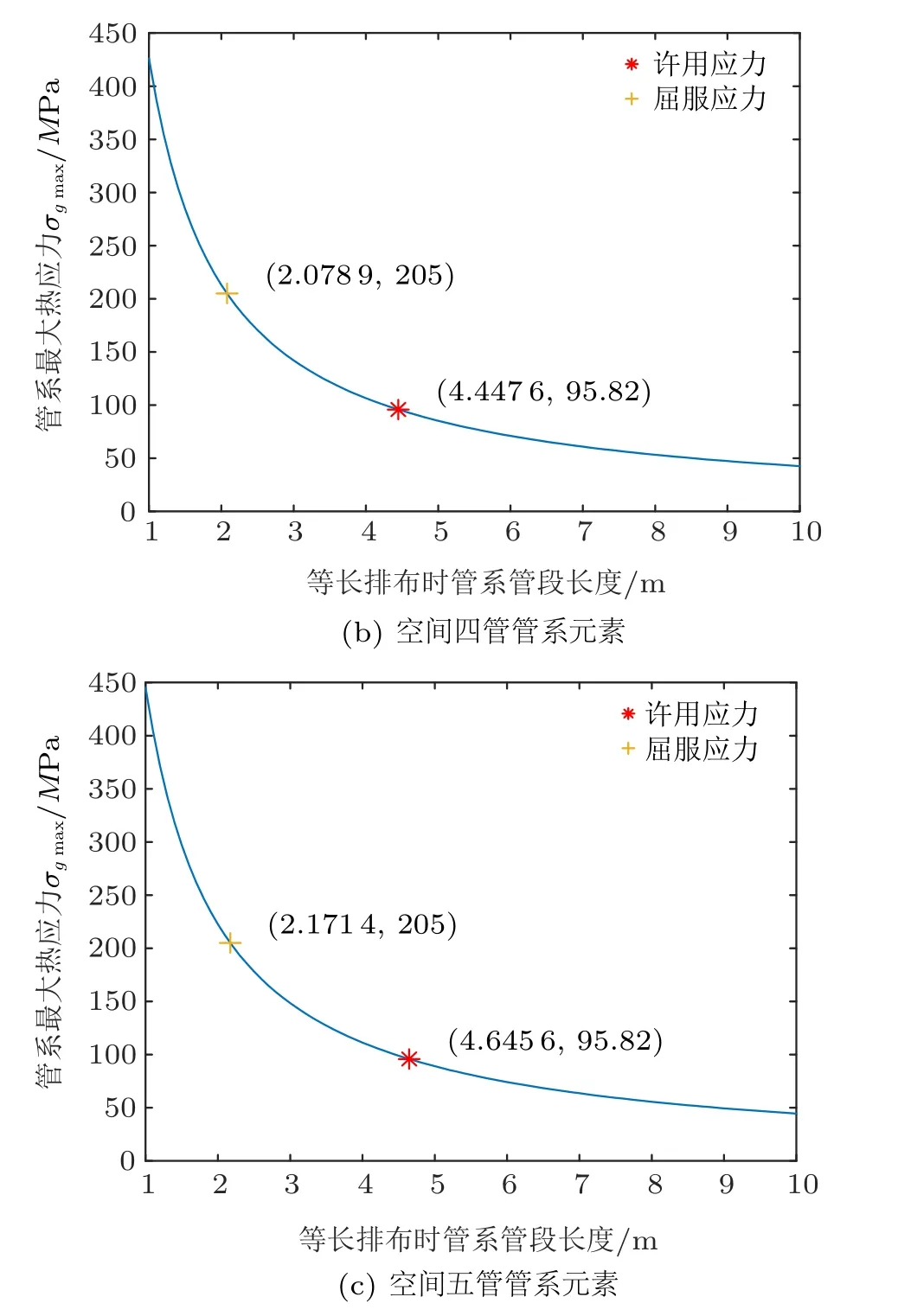
图10 管系等长排布时管段长度与最大热应力的关系

若继续增加管系管段数目，以等长排布管系的管段数目n为横坐标，以在许用应力/屈服应力范围下等长排布管系所允许的最小管段长度Lmin为纵坐标，不同的曲线分别表示许用应力/屈服应力的条件，经过Matlab 计算，得出图11 的变化趋势。

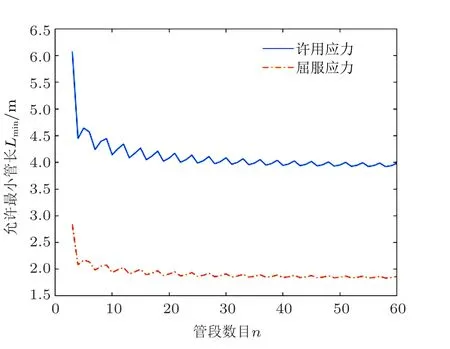
图11 等长排布管系管段数目对其最小允许管长的影响

表1 列出了图10 和图11 的部分数据。

表1 管系等长排布时允许的最小管段长度

表1 中n表示管系管段数，Lmin([σ]) 为许用应力范围内允许的管系最小管段长度，Lmin(σs) 为屈服应力范围内允许的管系最小管段长度。由此，若已知管系的管道参数以及材料工作温度下的许用应力[σ]或材料屈服应力σs，即可根据上述过程大致界定管系所允许的最短管长，一旦管系中有管段长度短于Lmin，那么不论管系如何排布管段，均不能使管系的最大热应力满足许用应力/屈服应力的条件。

由表1 和图10 可以看出，等长排布管系允许的管段最短长度随着管段数目的增加虽然有起伏，但总体趋势是变短的，且其有一个趋近值，在许用应力的范围内，最短管长度趋近于4 m 左右，在屈服应力的范围内，最短管长度趋近于2 m 左右。

3.3 管系最短管长度确定时允许的最大管段长度比

根据3.2 节的分析，以许用应力为条件的管系允许的最短管段长度大致为4 m。分别以屈服强度σs= 205 MPa，流变强度σf= 305 MPa，抗拉强度σb=405 MPa 作为条件探讨管系允许的最大管段长度比。

若确定管系的最短管段长度为4 m，结合图8，可以得出在屈服应力、流变应力、抗压应力范围下管系所允许的最大管段长度比。仍以A335P91 钢材为例，经过Matlab 计算，得出图11 的变化趋势。图中横坐标为空间管系相邻管段最大长度比RL，纵坐标为同管段长度比下各种排布方式中最大的热应力σgmax，图中点的横坐标为σgmax最接近管系材料(A335P91 钢材) 的屈服应力、流变应力、抗压应力时的管系管段长度比。

由图12 可以得出管系最短管段长度为Lmin=4 m 时，在热应力不超过屈服应力、流变应力、抗拉应力的条件下，所允许的最大相邻管段长度比如表2。

表2 中n表示管系管段数，RLmax(σs) 为屈服应力范围内允许的最小管段长度，RLmax(σf) 为流变应力范围内允许的最小管段长度，RLmax(σb) 为抗拉应力范围内允许的最小管段长度。由此，若管系的最短管段长度确定，且已知管系的管道参数以及材料的屈服应力σs、 流变应力σf或抗拉应力σb，即可根据上述过程大致界定管系所允许的最大管段长度比，若管系管段长度比不大于RLmax(σs)(RLmax(σf)，RLmax(σb))，那么无论管系如何排布管段，管系最大热应力都能满足屈服应力(流变应力、抗拉应力) 的条件。一旦管系管段长度比大于RLmax(σs)(RLmax(σf)，RLmax(σb))，那么在各种管系排布管段的方式中，将可能出现最大热应力超过屈服应力(流变应力、抗拉应力) 的请况，且管系管段长度比RL越大，这种可能性也越大。

若确定管系最短管长为4 m，并依次探究在屈服强度、流变强度和抗拉强度的条件下，管系最短管长确定的条件下允许的最大管段长度比RL与管系管段数目n的关系(图13，表3)。

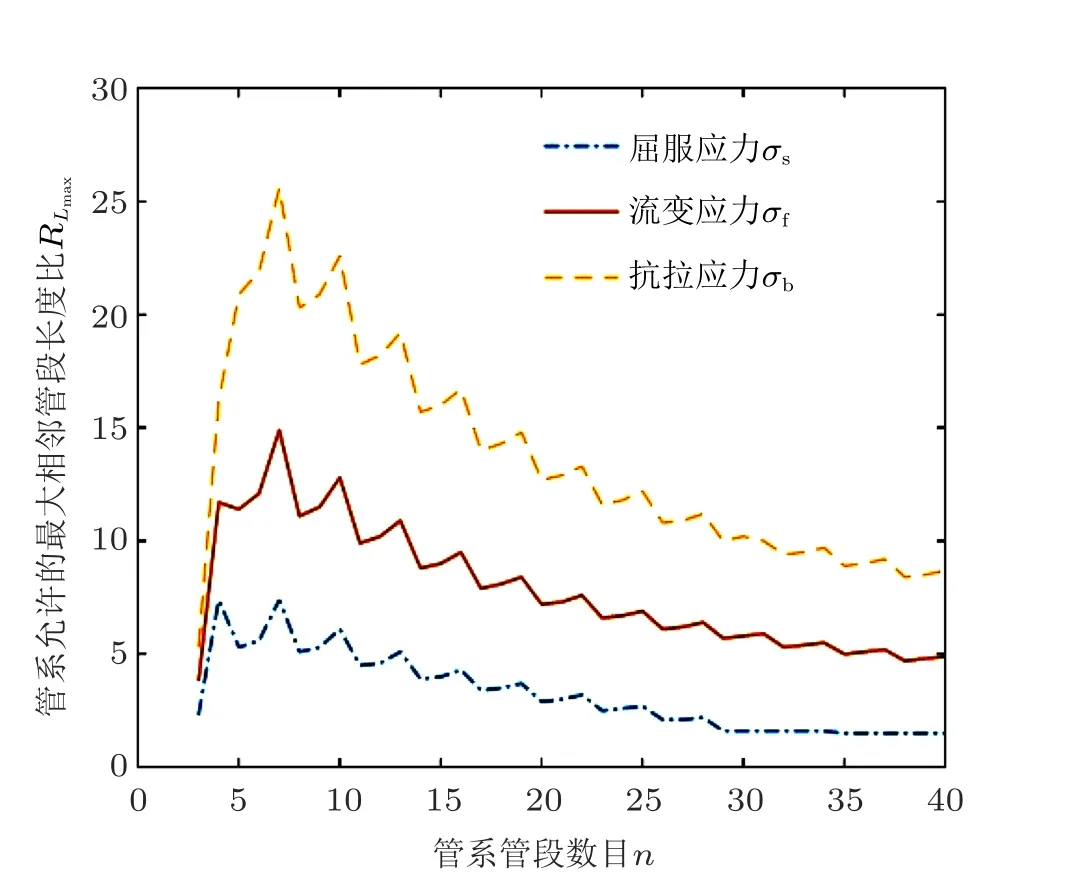
图13 各强度条件下允许最大管段长度比与管段数目的关系

表3 各应力范围下允许的最大管段长度比

由图13 和表3 可以得出，管系最短管长确定时，当管系的管段数目在一个合理的范围内时，管系允许的最大管段长度比较大，意味着管系有更多满足强度条件的管段排布方式。随着管系数目的增多，管系允许的最大管段长度比的整体趋势是减小的，原因可能是，当管系管段数目过多时，虽然相邻管段的长度差不大，但各个管段的差异会累加，最后使得整个管系结构在X，Y，Z三个方向的长度差异较大，导致管系的最大热应力较大。由图14 和表3 可以看出，虽然随着管系数目的增多，管系允许最短管段长度逐渐减小且有个趋近值：以屈服应力σs=205 MPa 为条件时，最大管段长度比趋近于1.5。以流变应力σf=305 MPa 为条件时，最大管段长度比趋近于5。以抗拉应力σb=405 MPa 为条件时，最大管段长度比趋近于8.5。

3.4 结论

结合Hovgaard 双弯管、空间四管管系以及空间五管管系元素的分析，在管道钢材料理想弹性且各向同性，管系两端固支，不计自重，且管系各管段可看作梁模型(即L/r不太小)的前提下，对空间管系元素有如下结论。

(1)管系相邻管段长度比越大，各种排布方式中的最大热应力也越大。

(2)以目前广泛使用的P91 管道为例，得出管系所允许的最小管段长度为4 m。

(3)在管系最小管段长度4 m 的前提下，进一步得出管系分别对应于屈服应力、流变应力和抗拉强度所允许的最大管段长度比。

(4)管系允许的最短管长随着管段数目的增加总体是变短的趋势，且其有一个趋近值。

(5)在管系最小管段长度确定的前提下，管系允许的最大管段长度比随着管段数目的增加总体趋势是变小的，且其有一个趋近值。

(6)对于实际广泛应用的再热热段蒸汽管道(A3-35P91 钢材为例，管道外径d= 335.05 mm，管壁厚t= 30 mm，弹性模量E= 154.7 GPa，膨胀系数α= 13.009× 10-6K-1，管道的工作温度由20°C 变化到546°C，工作温度下的许用应力[σ] = 95.82 MPa，材料屈服应力σs= 205 MPa，抗拉强度σb=405 MPa。)，我们建议，在高温管系设计中，相邻管段的长度比不能大于8，应尽量控制在5 以内，理想状态是不超过3。