计及线路气象随机性的电网电热协调潮流模型
2021-05-07应展烽刘天明
祖 玮, 应展烽, 徐 冰, 刘天明
(1.南京理工大学能源与动力工程学院, 南京 210094; 2.南京南瑞集团公司, 南京 211000)
传统电力系统分析中,常以导线热定值判断架空输电线路是否处于安全运行状态。导线热定值主要包含静态热定值(static thermal rating, STR)和动态热定值(dynamic thermal rating, DTR)两类[1-2]。STR是指在低风速、高环温和强日照等恶劣气象条件下所确定的线路载流量,而DTR是考虑了气象条件实际变化的线路载流量。STR的设定相对保守,极大低估了线路输送能力。DTR在一定程度上提升了线路输电容量,但仍是一种电流形式的约束条件,无法进一步提升线路输电能力。
在此背景下,加拿大学者Galina于2005年提出了电网电热协调(electro-thermal coordination, ETC)理论的概念与实现框架[3-4]。ETC理论的基本思想是将输电线路导线温度作为电网关键状态变量,融入电网运行分析和决策制订中。由于ETC理论将线路输送能力限制回归为导线温度约束,故可利用导线温升的热惯性效应,充分挖掘线路输电潜能,最大程度提升电网运行经济性。因此,ETC理论有效克服了STR和DTR的不足,可促进电网规划、调度和新能源消纳等技术的进一步发展[5-16]。
从潮流计算角度看,ETC理论能够同时获得电网潮流分布和线路温度计算结果,可更为有效地分析电网运行状态,更为合理地制订电网运行策略。因此,近年来已有不少学者对ETC潮流模型开展了研究。例如:文献[11]研究了ETC潮流模型及其算法,并分析了输电线路温度的变化过程;文献[12]将ETC潮流模型引入至电缆输电网中,并分析了电缆线路运行的热安全性;文献[13]在文献[3-4]的基础上提出了ETC潮流模型,计算结果表明线路温度变化对潮流结果具有一定程度的影响。
在实际工程中,架空输电线路导线温度的波动与环境气象变化的随机性密切相关。然而,在现有ETC潮流模型中,线路所处环境气象大多被假设为确定的已知参数。因此,传统ETC潮流模型只能计算当前时刻下的电网潮流和导线温度,无法体现电网各状态量的随机变化规律,也无法分析电网运行过程中的线路热过载风险。
为此,现将马尔科夫链方法与传统电热协调潮流模型相结合,提出了一种计及线路气象随机影响的ETC潮流模型。通过IEEE-9节点算例验证本文模型描述线路环境气象对电网潮流和导线温度的随机影响的有效性,从而反映电网运行时的线路过热风险。
1 传统ETC潮流模型
1.1 模型原理
ETC潮流模型以线路阻抗参数为纽带,将电网潮流方程和导线热平衡方程进行耦合求解,其具体表达式为

(1)
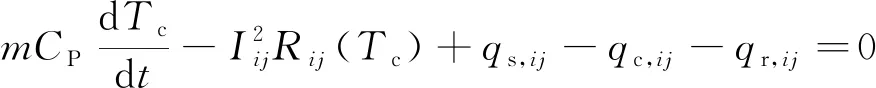
(2)
式中:n为电网总节点数,i和j为节点号,ij为节点i与j之间的线路编号;PGi和QGi分别为节点i处的发电机输出的有功和无功功率;PDi和PDi分别为节点i处的负荷有功和无功功率;Ui和Uj分别为节点i和j的电压幅值;θij=θi-θj为节点i和j之间的电压相角差;Gij(Tc)和Bij(Tc)分别为线路ij的电导和电纳,与导线温度Tc有关;Iij为线路ij的电流;m为单位输电导线的质量;CP为输电导线材料的比热容;Tc,ij为线路ij的导线温度;Rij(Tc)为单位长度导线的交流电阻值,与导线温度Tc有关;qs,ij,qc,ij和qr,ij分别为线路的日照吸热功率,对流散热功率和辐射散热功率。
可以发现,式(1)为电网潮流方程,体现了系统各节点的功率平衡。式(2)为导线热平衡方程,描述了输电线路导线的温度变化。因此,电热协调潮流模型能够同时获得电网潮流和线路温度的计算结果,可为电网运行分析和决策制订提供有力支撑。
1.2 电网潮流方程的参数确定
在式(1)所示电网潮流方程中,线路电导Gij(Tc)和电纳Bij(Tc)分别由式(3)和式(4)确定,即

(3)

(4)
式中:Xij(Tc)为线路ij的电抗,与导线温度Tc有关。
导线交流电阻Rij(Tc)的表达式为
Rij(Tc)=Rref[1+αH(Tc-Tref)]
(5)
式(5)中:Rref为基准温度Tref下的导体直流电阻,基准温度通常取为20 ℃;α为电阻温度系数。
导线电抗Xij(Tc)的表达式为

(6)
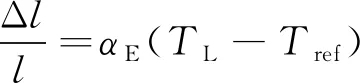
(7)
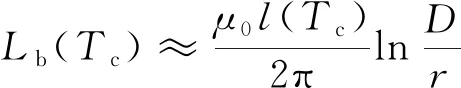
(8)

(9)
式中:μ0为磁场常数;l为导线常数;r为导线的计算半径;D为三相导线的几何平均距离,其单位与r的电位相同;ε0为电场常数;温度系数αE取23.1×10-6K-1;Δl为导线受热伸长量;Cb(Tc)和Lb(Tc)为单位长度导线且导线温度为Tc时的电容和电感;TL为导线长度为L时的导线温度。
1.3 线路导线热平衡方程的参数确定
在式(2)所示导线热平衡方程中,电流Iij的计算式为

(10)
日照吸热功率qs,ij的表达式为
qs,ij=αsQsesin(θ)D
(11)
式(11)中:αs为导体吸热系;Qse为日照辐射强度,W/m2;D为导线直径,mm;θ为太阳入射的有效角度。
辐射散热功率qr,ij的表达式为
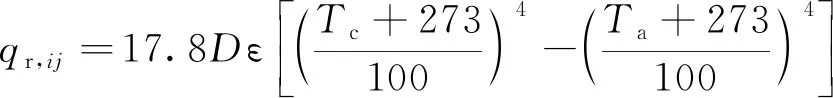
(12)
式(12)中:ε为导体表面的辐射系数,它主要取决于导线直径和材质及老化和氧化的程度,新导线辐射系数较低,一般为0.23~0.43,旧线或涂黑色防腐剂的导线则较高,为0.9~0.95。
热散热功率qc,ij与风速大小有关。其中,低风速、高风速和无风速条件下的计算表达式如式(4)~式(6)所示。
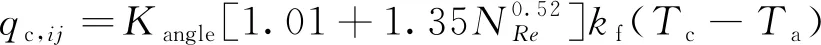
(13)

(14)
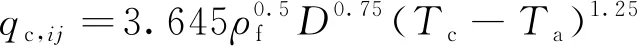
(15)
式中:Kangle为风向系数;NRe为雷诺数;kf为空气的热导率,W/(m·℃);Ta为导线周围实际环境温度;ρf为空气密度,kg/m3。
1.4 模型解法
ETC潮流模型的解法可通过潮流方程和热平衡方程交替求解实现[16],相关求解流程如图1所示。

图1 ETC潮流模型求解的流程图Fig.1 Flow chart of ETC power flow model
由图1可知,ETC潮流模型的具体求解步骤如下。
步骤1 依据线路温度,对潮流方程中的线路导纳参数Gij(Tc)和Bij(Tc)进行修正,初始线路温度设为27 ℃。
步骤2 通过经典牛顿拉夫逊方法计算电网潮流。
步骤3 依据潮流计算结果并结合热平衡方程,通过式(1)、式(2)和式(10),对线路温度进行计算。
步骤4 判断导线温度计算结果Tc是否收敛。若尚未收敛,则返回步骤1,直至导线温度Tc结果收敛。
步骤5 输出导线温度Tc和潮流结果。
2 所提ETC潮流模型
2.1 模型原理
由式(11)~式(15)可以发现,线路所处的风速、风向、环境温度和日照强度等气象参数是影响导线温度的关键变量。在传统ETC潮流模型中,上述气象参数通常被假设为确定值。因此,传统模型无法准确描述导线温度的变化规律,难以有预见性地估计电热协调潮流变化,也难以正确评估电网中线路运行的安全性。为此,提出了一种计及气象随机影响的ETC潮流模型,其基本结构如图2所示。
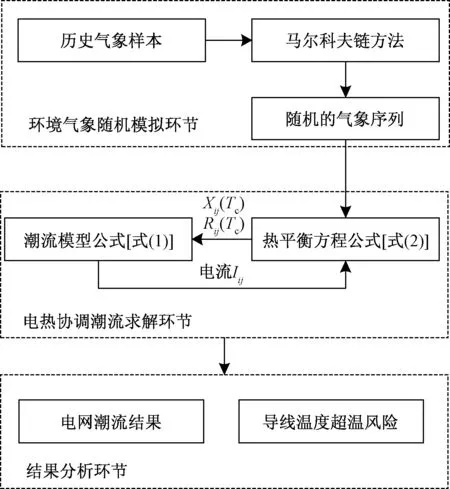
图2 所提模型结构图Fig.2 The structure chart of the proposed model
由图2可见,本文模型由环境气象随机模拟、ETC潮流求解和结果分析三个环节组成,其基本思想为:首先基于历史气象样本和马尔可夫链方法,实现线路气象的随机模拟;随后将气象模拟结果代入导线热平衡方程中,并通过图1所示求解方法交替求解热平衡方程和潮流方程;最后,对ETC潮流结果进行分析,获得电网潮流和导线温度的变化规律。
容易发现,本文模型在传统模型基础上,引入了环境气象的随机模拟。因此,该模型是一种ETC框架下的概率潮流模型,能够在计算电网潮流的同时,有效把握潮流与线路导线热安全性之间的联系。
2.2 马尔可夫链原理
马尔可夫链是一种离散随机过程的有效描述方法。该方法具备无记忆特性,可在当前信息给定的前提下模拟随机序列的发展过程,常被用于模拟气象的随机变化情况[17-20]。
设Xn为一个离散随机过程,而E{a1,a2,…,am}为一个离散集合。当存在Xn∈E时,则称E中的元素为随机过程Xn的状态。若Xn在n+1时刻的状态值ai只与其n时刻的状态值aj有关,与其他时刻无关,那么随机过程Xn便被称为一个马尔可夫链过程。该随机过程的状态取值满足如下条件概率:
pij=p{X(n+1)=ai|X(0)=a0,…,X(n-1)=an-1,X(n)=aj}=p{X(n+1)=ai|X(n)=aj}
(16)
式(16)中:pij为由状态aj转移状态ai的转移概率。
若随机过程的状态空间由L个状态组成,所有转移概率即可组合为矩阵的形式,即
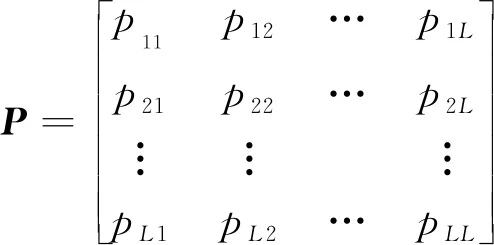
(17)
式(17)中:P为马尔可夫链的状态转移概率矩阵。通过相关历史数据建立矩阵P后,便可通过该矩阵中的各元素取值实现离散随机过程的模拟。
3 算例及分析
3.1 算例系统
为了验证本文模型的有效性,采用图3所示的IEEE-9节点系统进行算例分析。该算例系统基准电压和容量分别选取110 kV和100 MVA。

图3 IEEE-9节点电力系统图Fig.3 Diagram of IEEE 9 bus test system
为了便于结果分析,在不影响本文模型有效性验证的基础上,对算例系统进行如下假设:①系统中各条线路导线类型均为LGJ400/35;②系统中各条线路处于相同随机特性的气象条件下;③系统中各节点上负荷的有功功率及无功功率为恒定值。基于上述假设,表1~表3分别给出了导线热参数、线路初始电参数和各节点负荷参数。

表1 导线的热系数

表2 线路初始参数

表3 节点负荷参数
3.2 气象随机模拟的验证
为了验证本文模型中气象随机模拟的有效性,收集了图4所示的线路环境气象数据。上述气象数据均来自某供电公司的实测数据,总时间跨度为2019年3月—5月(共90 d)。其中,前60 d数据作为气象历史样本,用于建立环境气象的马尔可夫链。后30 d数据则作为验证样本,用于验证气象随机模拟的有效性。

图4 某供电公司的线路气象实测数据Fig.4 Meteorological data supposed by a power supply company
将历史样本划分为30个状态,并依据马尔科夫链原理,得到线路环境气象的状态转移概率矩阵,如图5所示。图中结果反映了各环境气象变化的随机特性。

图5 气象历史样本序列的马尔科夫链状态转移概率Fig.5 Diagram of Markov chain state transition probability based on historical weather conditions
利用状态转移概率对环境气象进行2 500次随机模拟,并统计得到模拟结果的状态转移概率矩阵。图6给出了气象验证样本和模拟结果之间的状态转移概率偏差。可以发现,相关偏差不超过10%。这也表明,马尔科夫链方法能够提供与真实数据变化规律相似的气象随机模拟结果。

图6 历史序列和验证序列马尔科夫链状态转移概率的偏差Fig.6 The relative difference between the Markov chain state transition probability of historical and simulated weather conditions
事实上,除马尔科夫链方法外,工程上还可采用概率分布模型模拟气象的随机特性。例如,风速、风向、日照和环境温度等气象参数的随机性可分别用Weibull分布、Cauchy分布、Beta分布、正态分布等分布模型描述[21-23]。为了体现本文模型的优势,图7给出了基于概率分布模型所得的气象状态转移概率的偏差结果。与图6对比可见,基于概率分布模型所得气象状态转移概率偏差明显高于马尔科夫链方法所得偏差。这是因为概率分布模型关注某个特定时间断面上的气象随机性,难以准确描述气象随时间变化的随机规律。因此,本文方法良好反映了线路气象状态变化的随机过程。
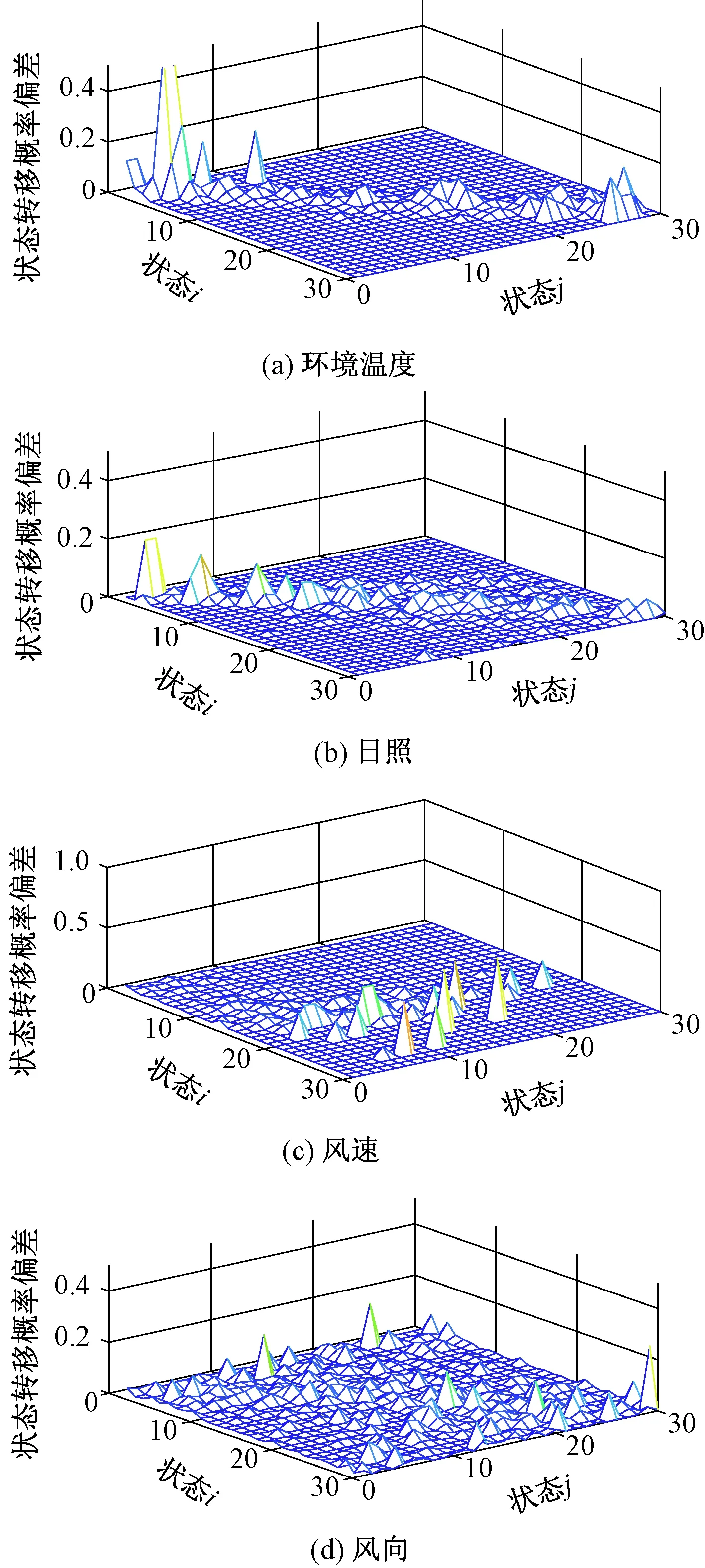
图7 基于概率分布模型所得的气象状态转移概率偏差Fig.7 The probability deviation of meteorological state transition based on probability distribution model
3.3 本文模型结果分析
下面分别利用传统ETC潮流模型和本文模型对算例系统进行潮流分析。由于传统ETC潮流模型忽略了线路气象的随机性,故导线热平衡方程中的气象参数均采用历史样本的平均数据。
表4和表5分别为两类ETC潮流模型所得系统各节点电压幅值和相角值(节点1为平衡节点,其电压幅值与电压相角已知)。而图8和图9则分别为在相同负荷条件下两类ETC潮流模型所得各线路温度的变化情况。对比上述数据可见,传统ETC潮流模型忽略了环境气象对线路温度的不确定性影响,故所得线路温度结果较为平滑,所得节点电压幅值及相角也均为确定值。这表明,传统ETC潮流模型无法描述线路温度在环境气象作用下的随机变化,也无法体现因线路温度变化而引起的电网状态量随机波动。相反,本文模型计及了环境气象对线路温度的随机影响,并通过线路参数将该影响与系统电压幅值和相角的变化进行了关联,故可以得到电网状态量的统计规律。因此,本文模型有效反映了线路气象随机特性对电网潮流和线路温度结果的影响。

表4 传统ETC潮流模型所得节点电压幅值和相角
下面设导线最高允许运行温度为70 ℃,并利用本文模型对系统线路温度进行2 500次估计,从而统计得到各线路的热过载概率,如图10所示。为了验证结果的有效性,图10中还给出了基于气象验证样本所得线路热过载概率。由本文模型计算结果可知,本算例系统中的线路L57、L69和L78具有较高过温风险,相关热过载概率可达51.9%、32.1%和42.7%。上述结果与实测气象数据下的线路热过载概率较为吻合。这也表明,本文模型不仅能够获得系统潮流的统计规律,还可有效获取输电线路的过热风险。

表5 本文模型所得节点电压幅值和相角
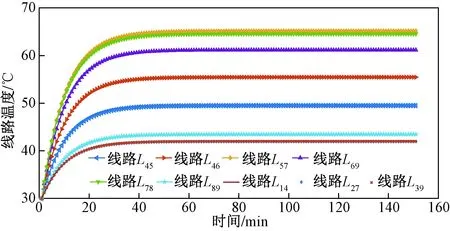
图8 传统ETC潮流模型所得线路温度曲线Fig.8 Line temperature curves obtained from the traditional ETC power flow model
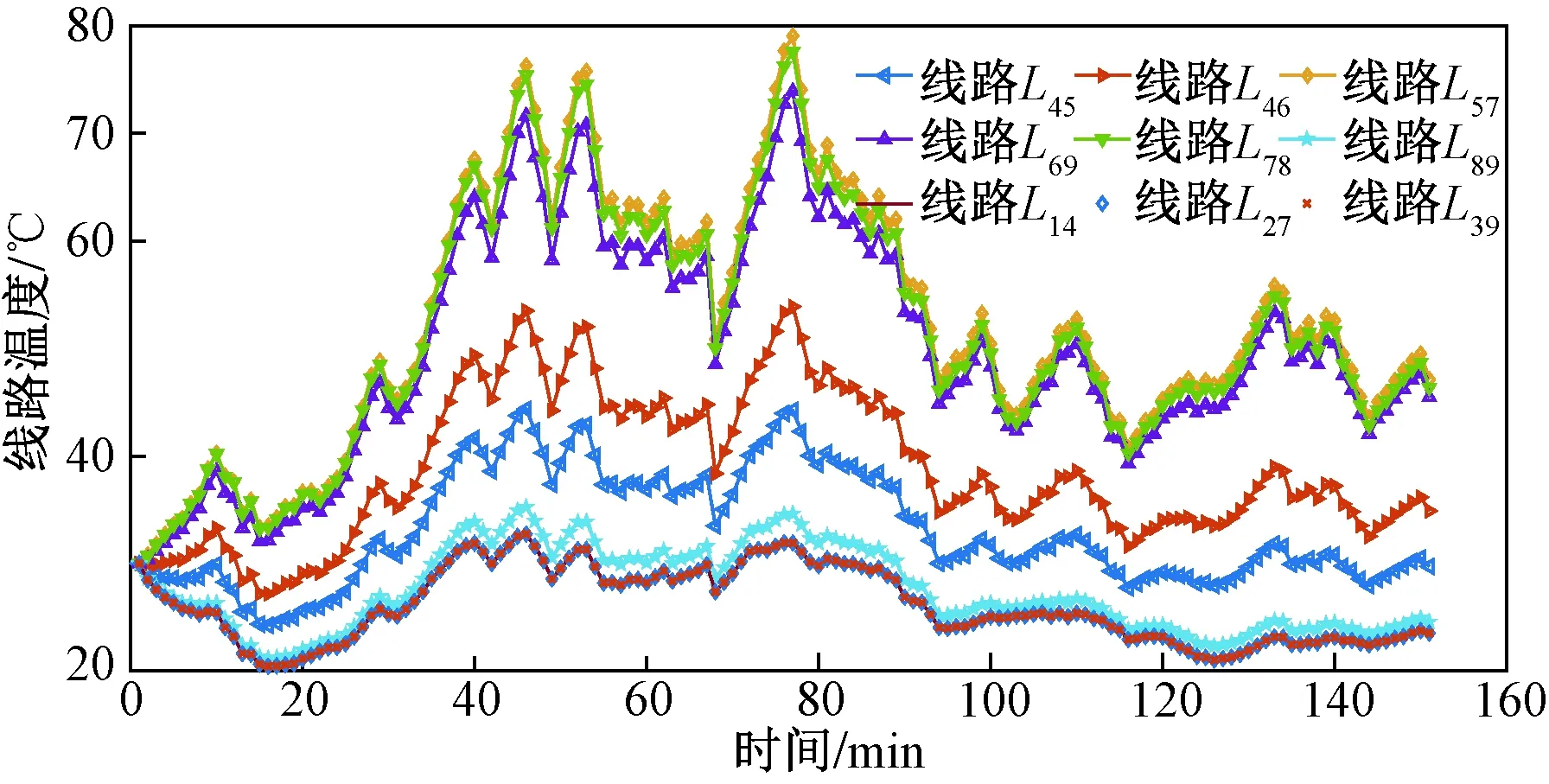
图9 本文模型所得线路温度曲线Fig.9 Line temperature curves obtained from the ETC power flow model proposed in this paper
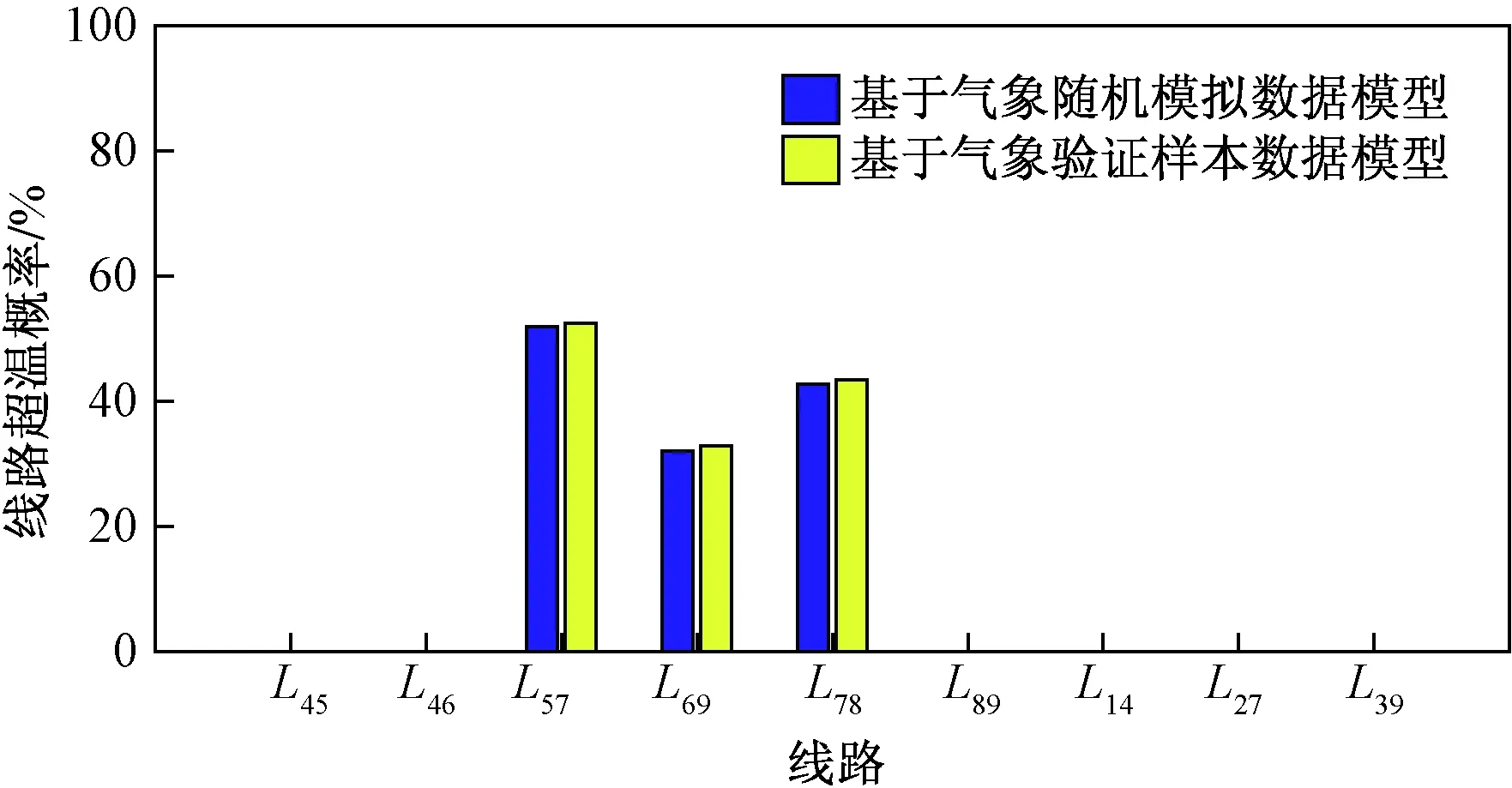
图10 导线超温概率Fig.10 Probability of line overtemperature
4 结论
在传统ETC潮流模型基础上,通过引入环境气象随机模拟方法,提出了一种计及线路气象随机影响的ETC潮流模型,并通过IEEE-9节点算例系统进行了验证。所得结论如下。
(1)本文模型能够在计算电网潮流的同时,准确描述气象随机性对导线温度变化影响。
(2)本文模型能够有效反映潮流与线路过热风险之间的关系。
(3)本文模型仅考虑了环境气象随机性对ETC潮流的影响。未来可以结合电网负荷和发电量的随机特性,进一步开展电热协调潮流模型的研究,使电网运行的决策制订更加合理。
