基于混沌映射和置换有序二进制编码的密文域可逆信息隐藏

林文兵， 张敏情， 周 能， 孔咏骏

(武警工程大学网络与信息安全武警部队重点实验室， 西安 710086)

可逆信息隐藏技术[1-2]是信息隐藏研究领域的重要分支，是接收方在正确提取信息后，还能无差错地恢复原始载体。严格来讲，它属于一种脆弱水印。因此，通常应用于远程医学、司法取证等领域。近年来，可逆信息隐藏技术得到不断的发展，目前有三种典型的嵌入方式：无损压缩[3-4]、差分扩展[5-6]和直方图平移[7-9]。Thodi等[10]提出了预测误差扩展算法。此后，该算法得到不断的改进，如直方图平移和预测误差扩展相结合等。

随着黑客攻击，网易邮箱泄露等信息安全事件的频繁发生，密文域可逆信息隐藏受到了广泛的关注[11-13]。它要求用于嵌入信息的载体是经过加密的，并且在正确提取信息后能无损地恢复原始载体。同时，由于云服务的推广，密文域可逆信息隐藏技术作为密文信号处理技术与信息隐藏技术的结合也得到了持续的研究。

为了提高嵌入容量，Ma等[14]提出了加密前预留空间的方法，通过将像素值的最低有效位嵌入到其他像素值中，从而得到预留空间进行信息嵌入。虽然该方法可以提高嵌入容量，但是存在发送方不能提前知道嵌入信息的长度和复杂预处理增加系统负担的问题。因此，不能满足实际应用。相反，加密后预留空间[15-17]是对加密后的像素进行修改，从而得到预留空间。Zhang[15]提出加密后预留空间的方法，通过翻转每个块中的三个最低有效位，从而进行信息的嵌入。Hong等[16]通过更好地运用空间相关性，将Zhang的算法进一步改进。Zhang[18]提出了可分离算法，即接收方可以在明文和密文上正确提取秘密信息。Qian等[19]运用信源分布编码将Zhang的方法进一步改进。Ren等[20]将置换有序二进制(permutation ordered binary，POB)编码技术引入密文域可逆信息隐藏。

受文献[20]的启发，为了进一步解决嵌入信息时造成溢出问题和加密后图像分块内仍存在一定的相关性问题。同时，提高秘密信息的嵌入容量。现将混沌映射和POB编码运用于密文域可逆信息隐藏。首先，图像拥有者运用混沌映射对原始图像进行加密，得到加密图像。然后，数据隐藏者对加密图像进行预处理后，运用POB编码技术在满足嵌入条件的像素点上进行秘密信息的嵌入。以期实现秘密信息的正确提取和原始图像的无损恢复。

1 相关知识

1.1 POB编码系统

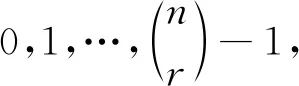
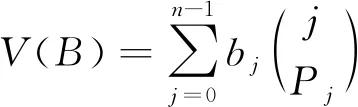
(1)

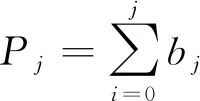
(2)

式中：i为二进制字符串的位置；j为POB编码系统中的数值位置；bj为二进制字符串各个位置的数值，如0或1；Pj为二进制字符串各个位置的数值之和；V(B)为POB编码系统中的数值。

1.2 混沌映射系统

1.2.1 Logistic映射

Logistic映射[22]是一种非线性方程，具有混沌特性，可表示为

xn+1=uxn(1-xn)

(3)

式(3)中：u为控制参数，取值范围为[0,4]；xn为输出的混沌序列。

1.2.2 Sine映射

Sine映射与Logistic映射相类似，也具有简单的混沌特性，可表示为

xn+1=rsin(πxn)

(4)

式(4)中：r为控制参数，取值范围为(0,1]；xn为输出的混沌序列。

1.2.3 改进的混沌映射

张静等[23]为了解决区间受限和点分布不均匀问题，将Logistic映射和Sine映射结合越来，得到改进后的混沌映射，可表示为

xn+1=r{usin(πxn)[1-sin(πxn)]×2kmod1}

(5)

式(5)中：r= 20；k为控制参数，取k= 18。

2 算法设计

基于混沌映射和POB编码的密文域可逆信息隐藏算法流程如图1所示。

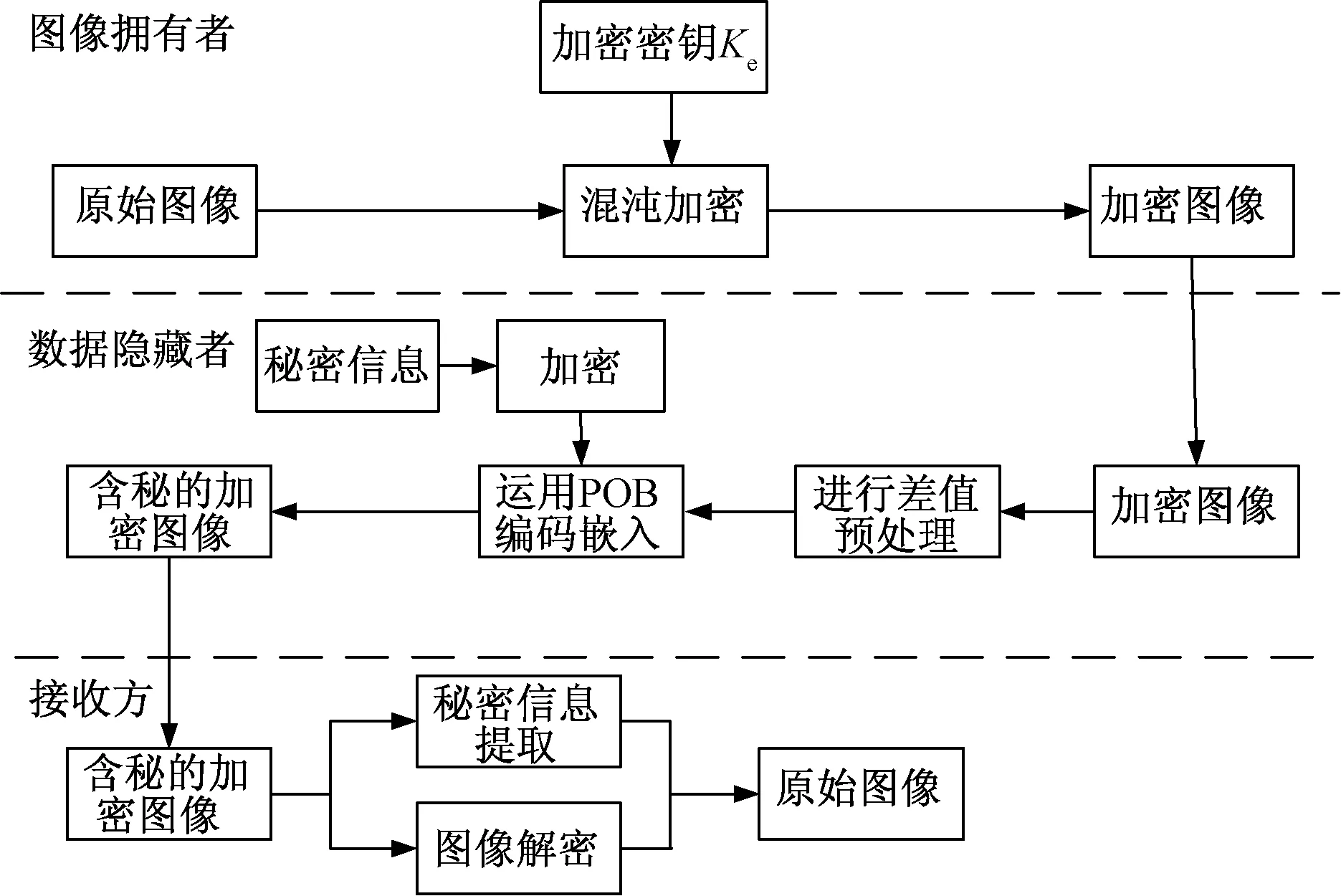
图1 方案流程图Fig.1 Scheme flow chart

2.1 初始化与加密

2.1.1 混沌系统初始化

在图像加密过程中，由SHA-256哈希函数生成一个256位的密钥K。将该密钥等分成32组。如K=k1,k2,…,k32,其中，ki= {ki,0,ki,1,…,ki,7}(i=1,2,…,32)。同时，通过密钥K和4个预设密钥可对混沌系统进行初始化，表示为

x=x0+

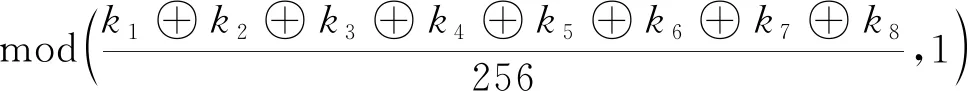
(6)

y=y0+

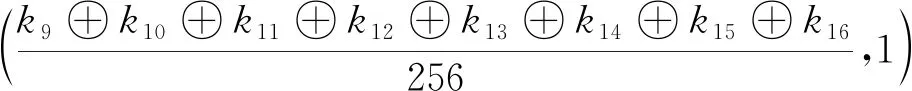
(7)

u=mod(u0+k17⊕k18⊕k19⊕k20⊕k21⊕

k22⊕k23⊕k24/256,1)

(8)

r=mod(r0+k25⊕k26⊕k27⊕k28⊕k29⊕

k30⊕k31⊕k32/256,1)

(9)

2.1.2 图像加密

图像拥有者将大小为M×N的原始图像I转化成大小为L的8位二进制图像I′，其中，L=M×8N。同时，通过混沌系统初始化得到的x、u、r代入式(5)中进行N+L次迭代。然后，舍弃前N次后可得到混沌序列S= {s1,s2, …,sL}，并将其按升序进行排列得到序列Sn= {sn,1,sn,2, …,sn,L}和相应的位置索引index = {d1,d2, …,dL}。将转化后的图像I′通过位置索引index进行置乱得到图像I″，表示为

I″i=I′di，i=1,2,…，L

(10)

同理可得，将混沌系统初始化的y、u、r代入式(5)中，经过N+L次迭代，得到序列XS。而后，通过式(11)，可得到扩散图像C。

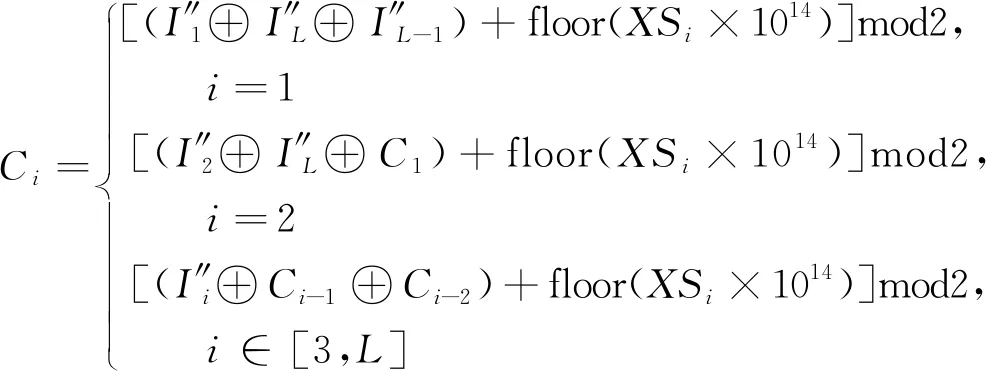
(11)

同时，将Ci进行合并可得到大小为M×N的图像Ic。再将混沌序列S、XS代入式(12)和式(13)中，可得S1、Xt，即

S1=mod[floor(1016S),M×N]+1

(12)

Xt=104XS-fix(104XS)

(13)

再将S1和Xt相加，组合成大小为16的数组bs,如式(14)所示。

bs(k)=S1(k2+80)+Xt(256k),k=1,2,…,16

(14)

将得到数组bs按升序进行排列，可得到相应的位置索引Tb= {tb1,tb2, …,tb16}。最后，将图像Ic分成16份，按位置索引Tb进行置乱，可得到密文图像Im。同时，将加密密钥K、初始值x、y、r、u和迭代次数N运用算术编码进行压缩后，嵌入到最后一行的最低有效位中。

2.2 差分直方图生成与信息嵌入

2.2.1 差分直方图生成

数据隐藏者收到加密图像后，将其划分成不重叠、大小为3×3的小分块。同时，标记为B(1,1)、B(1,2)、B(1,3)、B(2,1)、B(2,2)、B(2,3)、B(3,1)、B(3,2)、B(3,3)，并以中心像素点B(2,2)为参考像素点。分块内的参考像素与其相邻像素的差值可通过式(15)计算得到，即

di,j=B(i,j)-B(2,2),B(i,j)≠B(2,2)

(15)

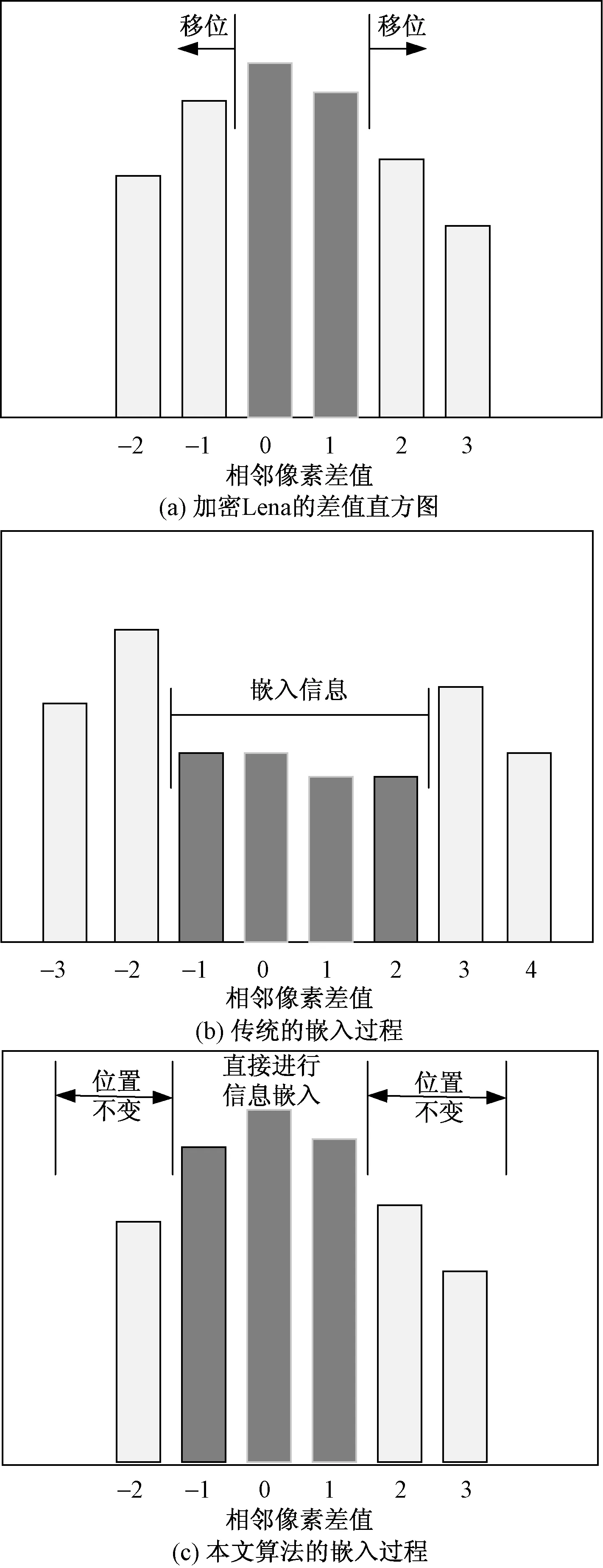
图2 传统的移位嵌入与本文算法的直接嵌入对比Fig.2 Comparison of traditional shift embedding and direct embedding of the algorithm in this paper

由于图像加密后仍存在一定的相关性，所以分块内相邻像素间的差值一般集中在[-1,1]，生成的直方图如图2所示。传统的运用预测误差扩展算法进行信息嵌入时，会先移位以腾出嵌入空间。而后，在差值为0或1上进行信息的嵌入。以Lena为例，嵌入过程如图2(a)、图2(b)所示。但是，传统的嵌入方法会不可避免地造成溢出问题或者会引入辅助信息，从而增加系统运算的负担。图2(c)是本文算法的嵌入过程，该方案在满足参考像素与其相邻像素的差值为-1、0、1时，在相应的像素点上直接进行信息的嵌入。同时，嵌入信息后不会产生溢出问题。

2.2.2 信息嵌入

对加密图像进行分块后，利用参考像素与其相邻像素之间的差值生成直方图。同时，通过差值直方图中-1、0、1的高度来预估可嵌入的容量。如果，待嵌入秘密信息的长度L大于可嵌入容量时，则不能进行信息嵌入的操作。如果，待嵌入秘密信息的长度L小于可嵌入容量时，则对每个满足条件的像素点进行秘密信息的嵌入。而后，利用POB编码系统转化为对应的POB值。根据POB编码的特性，如果向每个像素点中嵌入1 bit秘密信息时，则转化成POB系统中的最大值是125；如果向每个像素点中嵌入2 bit秘密信息时，则转化成POB系统中的最大值是251。所以，本文选择在每个满足条件的像素点中嵌入2 bit秘密信息，一方面不超过灰度图像像素的最大值，另一方面还提高了嵌入容量。最后，当秘密信息嵌入完成后，将秘密信息的长度L和像素点嵌入的比特数进行压缩，然后嵌入到参考像素点的最低有效位。为了便于理解，以下通过一个具体例子来说明。

如图3所示，以Lena大小为3×3的局部分块来细节说明信息嵌入的过程。首先，将加密后的像素值转化成相应的8位二进制。由于加密后的分块间仍存在一定的相关性。所以，以分块中B(2,2)=169为参考像素点，并与其相邻的像素作差，可得到相应的差值di,j。同时，判断该差值是否在[-1,1]范围内。如果不满足条件，则跳过该像素点，进行下一轮的判断。如果满足条件，则对该像素点进行2 bit秘密信息的嵌入。假设待嵌入的秘密信息是011110…011，则对满足条件的d1,2、d2,1、d3,1依次进行秘密信息的嵌入，使其转化成10位二进制的POB序列。然后，运用POB编码系统将POB序列进行无损压缩，而后转化成相应的POB值。最后，将嵌入后的像素点按原来的位置进行还原，得到含秘的加密图像。同时，将秘密信息的长度L和嵌入的比特数进行算术编码压缩，嵌入到参考像素的最低有效位中。

2.3 信息提取与图像还原

当接收方收到含秘的加密图像后，先将含秘的加密图像划分成不重叠、大小为3×3的小分块。而后，从分块中参考像素点的最低有效位提取出秘密信息的长度L和嵌入信息的比特数，并进行解码。其次，根据嵌入的比特数，将分块里的B(1,1)、B(1,2)、B(1,3)、B(2,1)、B(2,3)、B(3,1)、B(3,2)、B(3,3)转化成10位的POB序列。然后，取相邻像素点的前8位与参考像素点作差值。如果差值在[-1,1]范围内，则提取出后两位秘密信息。如果差值不在[-1,1]范围内，则该像素点没有进行信息嵌入操作。

在秘密信息提取完成后，从加密图像的最后一行中提取出加密密钥K、初始值x、y、r、u和迭代次数N。然后运用算术编码进行解压缩，根据得到的辅助信息，进行加密的反向操作就可以无损地恢复原始图像。

3 实验结果与分析

为了测试该算法性能，选用USC-SIPI图像库中大小为512×512的256级灰度图像进行实验，实验环境为：CPU: Intel(R) Core(TM) i7-8550U @ 2.00GHz, RAM: 16 GB, OS: Windows 10, Programming: MATLAB R2018a。并以4张测试图像来显示结果，如图4所示。主要从三个方面加密性能、嵌入容量与峰值信噪比和文献性能比较进行分析。

3.1 加密性能

利用混沌系统对图像进行加密，为了验证该算法加密的安全性和抗攻击能力，实验分析了加密图像的相关性、直方图和信息熵以及选择明文攻击下的鲁棒分析。为了更好演示结果，以Lena图像为例进行实验。

3.1.1 图像的相关性分析

原始图像的相邻像素之间具有一定的相关性，但是加密图像在理想状态下，相关系数几乎为0，如图5所示。

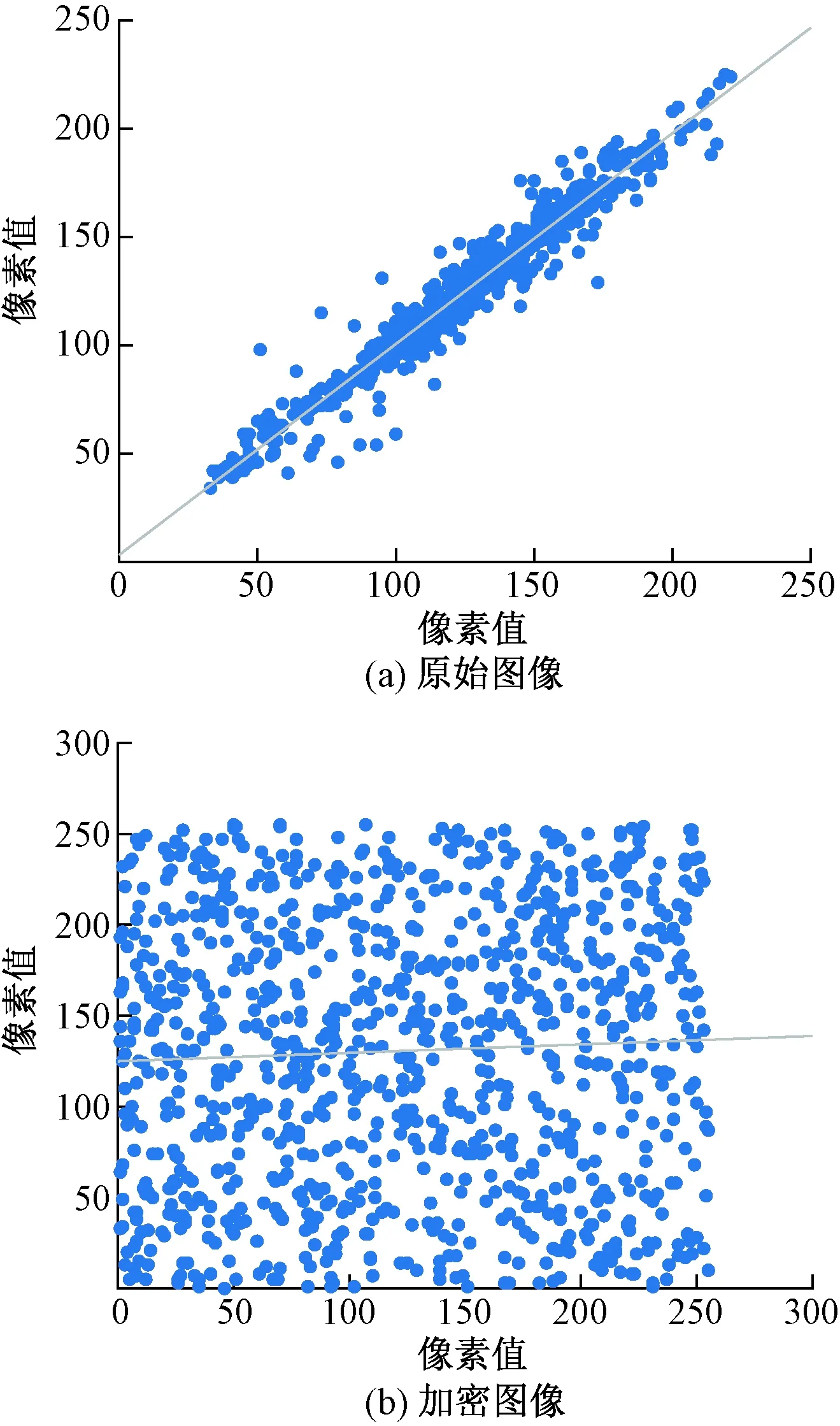
图5 原始图像与加密图像的相关性Fig.5 Correlation between original image and encrypted image

从图5可以看出，原始图像相关性比较明显，在对角线上的分布各不相同。然而，加密图像接近于随机均匀分布。因此，加密后不会造成信息泄露。

3.1.2 图像的信息熵分析

信息熵是系统有序程度的度量，不确定性越大，熵也就越大。因此，对原始图像和加密图像的信息熵进行分析。其中，信源s的信息熵计算公式为

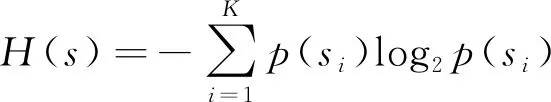
(16)

式(16)中：P(si)为像素si的概率。通过实验可得，原始图像和加密图像的信息熵如表1所示。

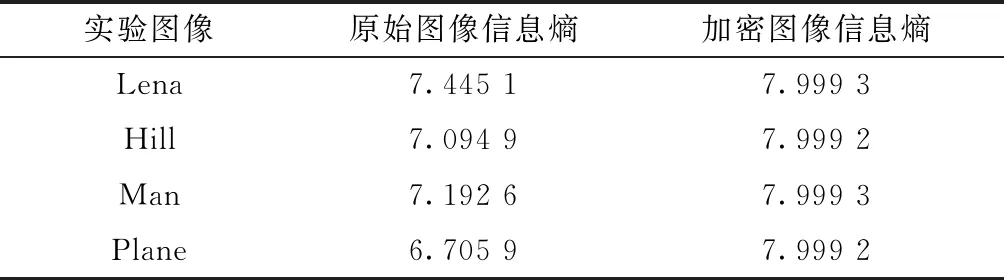
表1 原始图像与加密图像的信息熵

从表1中可以得出一般情况下，原始图像的信息熵比相应的加密图像小。在理想情况下，8位的灰度图像在加密后得到的信息熵等于8。本文运用混沌映射系统对原始图像进行加密后，图像的信息熵近似等于8。因此，原始图像在该加密算法进行加密后具有较高的安全性。

3.1.3 图像的直方图分析

直方图是图像的最基本的统计特征，用来表示图像中像素不同灰度值出现的频率。其中，Lena的原始图像与加密图像的直方图如图6所示。

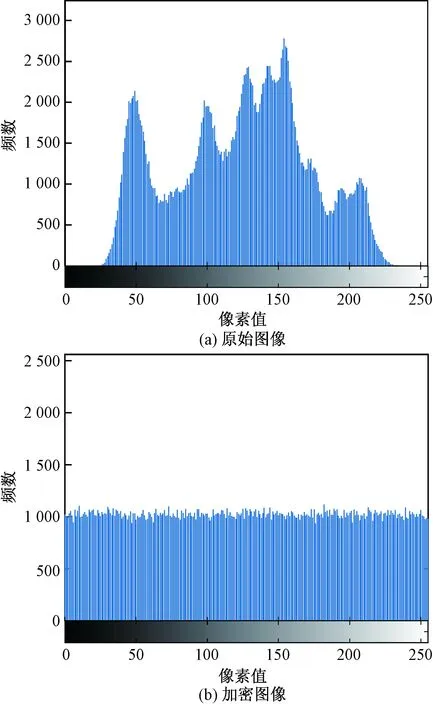
图6 原始图像与加密图像的直方图Fig.6 Histogram of original image and encrypted image

如图6所示，一般情况下，原始图像的直方图分布是不均匀的，具有较大的波动性。但是，加密图像的直方图分布是均匀的、一致的。因此，原始图像经过加密后得到的加密图像是安全的。

3.1.4 选择明文攻击下的鲁棒分析

已知明文攻击是指攻击者拥有用于待破解的密文相同密钥加密的一个或多个明密文对，密码学中认为选择明文攻击的难度比已知明文攻击要复杂。所以，只要能够抵抗选择明文攻击就能抵抗已知明文攻击。

图7 差异分析Fig.7 Difference analysis

如图7所示，虽然图7(b)相比于原始图像只改变了1 bit。但是，加密后的图像完全不同。所以选择任何图片运用混沌映射进行加密，都能抵抗选择明文的攻击。

3.2 嵌入容量与峰值信噪比

为了显示嵌入信息后图像的视觉变化，通常运用峰值信噪比(PSNR)来表示。其中PSNR可以通过式(17)和式(18)进行计算。同时，本文结合结构相似性(SSIM)对还原后的图像是否具有可逆性进行判别，结构相似性可通过式(19)计算。

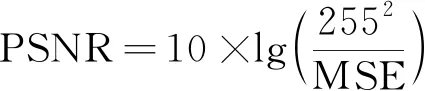
(17)

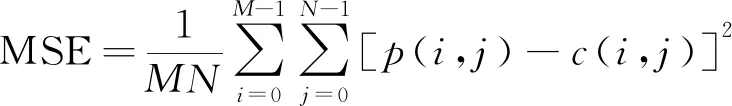
(18)

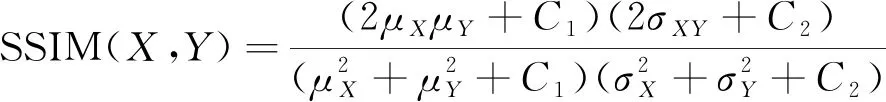
(19)

式中：M、N为图像的尺寸；p(i,j)为原始载体的像素值；c(i,j)为加密后图像的像素值；μX、μY为图像的像素；σX、σY为图像像素的标准差；σXY为图像像素的协方差。

通过测试图像在最大嵌入容量下进行PSNR、SSIM的测试。由于该算法只能在差值为[-1, 1]的范围内进行信息嵌入。所以，最大嵌入容量是可嵌像素点的2倍，即最大嵌入率Ec通过式(20)计算。如表2所示，4张测试图像本身平滑度各不相同，所以最大嵌入容量也不相同。由于Plane图像整体上较为平滑，分块内像素值差异较小。因此，最大嵌入容量可达到0.502 bpp(bits per pixel)。同时，还原后图像的PSNR = ∞，SSIM = 1，表明该算法具有真实的可逆性。

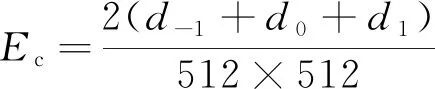
(20)

式(20)中：d-1为参考像素与相邻像素的差值为-1；d0为参考像素与相邻像素的差值为0；d1为参考像素与相邻像素的差值为1。

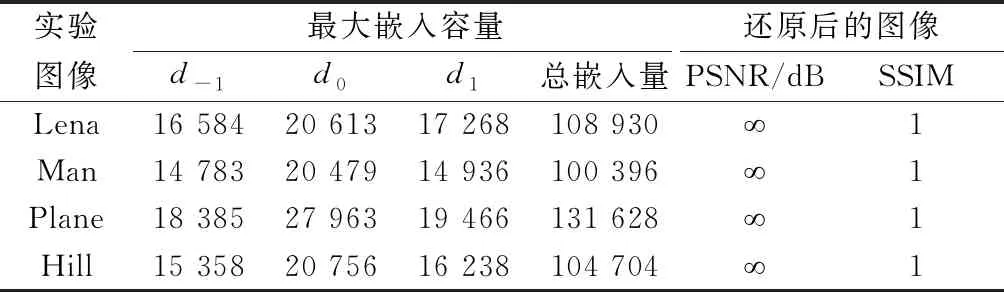
表2 加密图像中秘密信息的最大嵌入容量

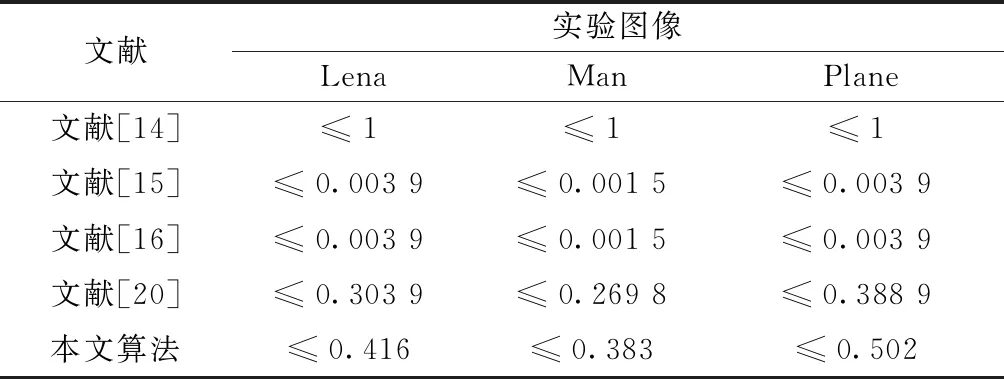
表3 本文算法与相关文献的最大嵌入率比较

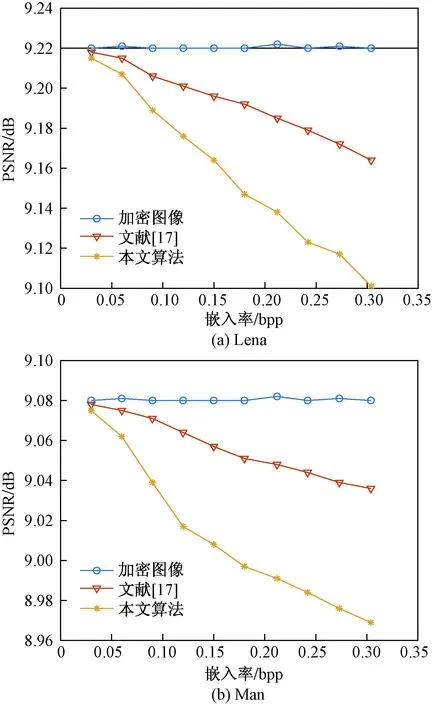
图8 不同嵌入率下加密图像中PSNR值的变化Fig.8 Changes in PSNR values in encrypted images at different embedding rates

从表3中可以得出，加密图像中的最大嵌入容量取决于图像的平滑度。同时，与近期相关文献相比，该算法的最大嵌入容量的优势比较明显。例如，在Lena图像中，运用本文算法进行信息嵌入，嵌入率相比于文献[20]提高了0.112 1 bpp。

3.3 文献性能比较

本小节主要对加密图像中相关性问题以及是否能无损恢复原始图像进行比较。假设向加密后的Lena、Man中嵌入79 665 bit秘密信息。从图8可以看出，文献[17]在最低有效位进行信息嵌入，会产生一些微小的变化。但是，运用POB编码进行信息嵌入后的PSNR会发生新的、较大的改变，从而进一步破坏块内的相关性,提高了加密算法的安全性。同时，本文测试了还原图像的准确率。从图9可以看出，与文献[15]和文献[18]相比，随着嵌入率增大时，文献[15]和文献[18]在图像还原过程中会存在失真情况。但是，运用POB编码进行信息嵌入，能够无损地恢复原始图像。

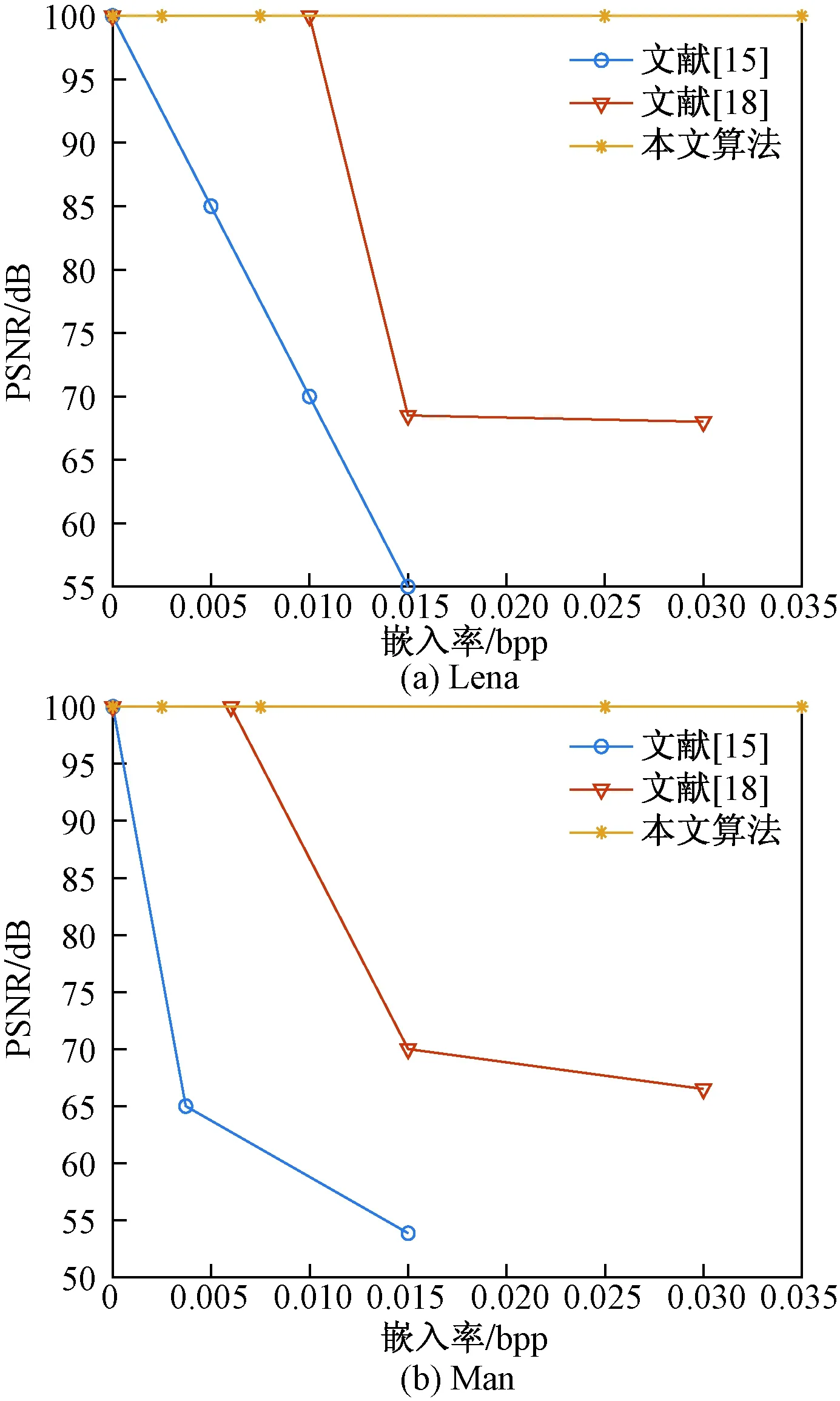
图9 不同嵌入率下还原图像的PSNR值Fig.9 PSNR values of restored images at different embedding rates

4 结论

将POB编码引进密文域可逆信息隐藏，不仅能够解决嵌入信息时造成的溢出问题，而且可以进一步破坏加密图像中的相关性。同时，运用参考像素点与其相邻像素点作差值，使得嵌入容量有了较大的提高。但是，运用POB编码进行信息的嵌入，会使直接解密的图像存在一定的失真。所以，下一步要研究在保证嵌入容量的条件下，如何提高图像的峰值信噪比。