煤矸光电分选输送机上料段物料冲击稳定性研究*

2021-12-07杨健王焕萍蒋庆楠张伟李飞

煤矿机电 2021年5期

杨健，王焕萍，蒋庆楠，张伟，李飞

(1.安徽理工大学机械工程学院，安徽淮南 232000；2.浙江西子富沃德电机有限公司，浙江杭州 311305)

0 引言

煤炭是我国主要能源之一，随着煤炭开采的同时，塌陷区又对地表环境造成破坏[1]。实现煤矸石的地下分选显得尤为重要，在提高原煤质量的同时，还能节省运费，进一步达到绿色采煤。现阶段，井下煤矸分选技术分为全粒级分选、煤矸分离和毛煤排矸3类，光电分选属于毛煤排矸，可将原煤中的矸石快速地排出，具有智能化、效率高、准确率高等优点[2]。近年来，国内外专家对煤矸石自动分选展开了大量的研究。2016年，50～300 mm大块煤智能分选机在晋煤集团赵庄煤业投入生产[3]。煤矸石运输至带式输送机时和输送带冲击后会产生反弹和滚动，输送带也相应会有一定振幅，导致光电分选时难以定位矸石的位置，影响分选的效果。史飞龙等[4]运用EDEM软件，建立了整个物料转运站，数值模拟了整个过程，得到了物料流对上料段的冲击力随时间变化的关系。徐瑞银等[5]对受料段的冲击特性进行分析，建立了输送带冲击动力学微分方程式，并对上料段结构参数进行优化。这些研究多是针对输送带受到的冲击力进行研究，而对于冲击后物料的运动状态尚未关注。上料段冲击引起的振动会破坏物料稳定性，对后续的定位分选不利。为了使煤矸石能够在输送带上保持稳定，现阶段采取的方法是延长带式输送机的长度，因此占用了过大的井下空间，降低了井下空间的使用率。

1 输送带材料本构模型

工程上对于橡胶材料的非线性力学问题，普遍假设橡胶材料具有各向同性，橡胶材料的本构关系可以用应变能函数W表达：

W=f(I1,I2,I3)

(1)

式中:I1、I2和I3为3个Green变形张量的不变量，基于应力—应变关系，如式(2)所示。

(2)

式中:λ1、λ2和λ3为轴向伸长比，对于不可压缩的材料，I3=1。

Yeoh提出一种模型，可以只根据单轴拉伸试验数据拟合参数来预测大变形的力学行为，描述的应变区域宽，适合于模拟橡胶大变形行为时应力应变关系。

Yeoh模型的应变能函数为[6]：

(3)

式中:N为多项式阶数；Ci0和Dk为材料参数，MPa；J为弹性体积比。

假设橡胶不可压缩，所以J=1，Yeoh应变能函数的三次项展开式为：

W=C10(I1-3)+C20(I1-3)2+C30(I1-3)3

(4)

式中:C10、C20和C30为材料参数，MPa。

根据应变能函数和式(2)，可得柯西应力张量σ为：

(5)

式中:p为假设橡胶不可压缩引入的水静压力，MPa。

(6)

将式(6)代入式(5)可得单轴拉伸柯西应力表达式为：

(7)

将式(4)代入式(7)可得：

(8)

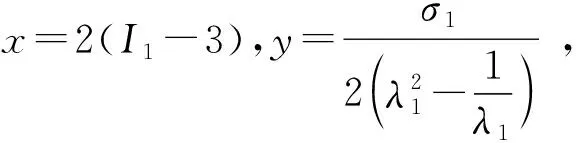
y=C10+C20x+0.75C30x2

(9)

式(9)中C10、C20和0.75C30为三次项式的3个系数，根据橡胶材料的应变和应力数据，通过MATLAB计算可得C10=1.505 9，C20=-0.050 4，C30=0.008 4。

将数据代入式(4)可得Yeoh应变能函数的三次项展开式为：

(10)

将式(10)中的数据添加进ANSYS材料库中，建立输送带橡胶材料。

2 有限元模型的建立

2.1 带式输送机上料段模型简化

假设冲击振动波仅在上料段传播，对带式输送机上料段进行简化，如图1所示。左端支撑为滚筒，右端支撑为托辊。带式输送机拉紧力为F，具有一个横向自由度且速度为v。

图1 带式输送机上料段简图

2.2 仿真模型及网格划分

如图2所示为在ANSYS/Explicit Dynamics中建立的有限元模型。将形状不规则的煤块简化为球体，研究单煤块下落首次冲击过程。A为输送带运动方向和速度，B和C为仅允许X轴方向滑动的约束，D和E为张紧力，F为重力。图3为网格划分示意图，煤块和输送带均用六面体网格，运用显式动力学方法求解。

图2 上料段仿真模型及边界条件示意图

图3 网格划分示意图

煤块的密度为1 400 kg/m3，泊松比为0.4，弹性模量为30 MPa，球状煤块直径为50 mm。输送带材料按照橡胶本构模型设置。假设煤矸石与输送带冲击时速度为3 m/s，方向与输送带垂直。分别设置输送带带宽为400 mm、500 mm、600 mm和700 mm，上料段长度为100～550 mm之间的变量，在ANSYS/ Explicit Dynamics中模拟煤矸石与输送带冲击过程，研究上料段长度和输送带带宽对煤矸石反弹速度和输送带振幅的影响。

2.3 碰撞过程分析

选取上料段长度400 mm，宽度220 mm。图4所示为下落过程示意图，小球与输送带碰撞，输送带中心向下凹并逐渐往外扩展。图5所示为反弹过程示意图，输送带收缩后将小球向上弹起，小球脱离输送带后输送带开始振动。

图4 下落过程示意图

图5 反弹过程示意图

3 结果与分析

3.1 上料段长度对煤矸石反弹速度的影响

图6所示为400 mm、500 mm、600 mm和700 mm带宽下煤矸石反弹速度与上料段长度的关系折线。上料段长度为100～200 mm时，反弹速度急剧下降;上料段长度为200～340 mm时，反弹速度随带宽的不同呈现出不同的趋势;上料段长度超过340 mm时，反弹速度基本不受带宽影响，且在0.15～0.3 m/s。总体呈反比例函数走势。

图6 反弹速度随上料段长度变化折线

3.2 上料段长度对输送带最大振幅的影响

图7为400 mm、500 mm、600 mm和700 mm带宽下输送带最大振幅与上料段长度的关系折线。上料段长度为100～240 mm时，输送带最大振幅与带宽关系不大；上料段长度超过240 mm时，输送带最大振幅随带宽的不同发生改变。其中，在上料段长度相同的情况下，输送带最大振幅随着带宽的增大有下降的趋势，但是下降的幅度越来越小。

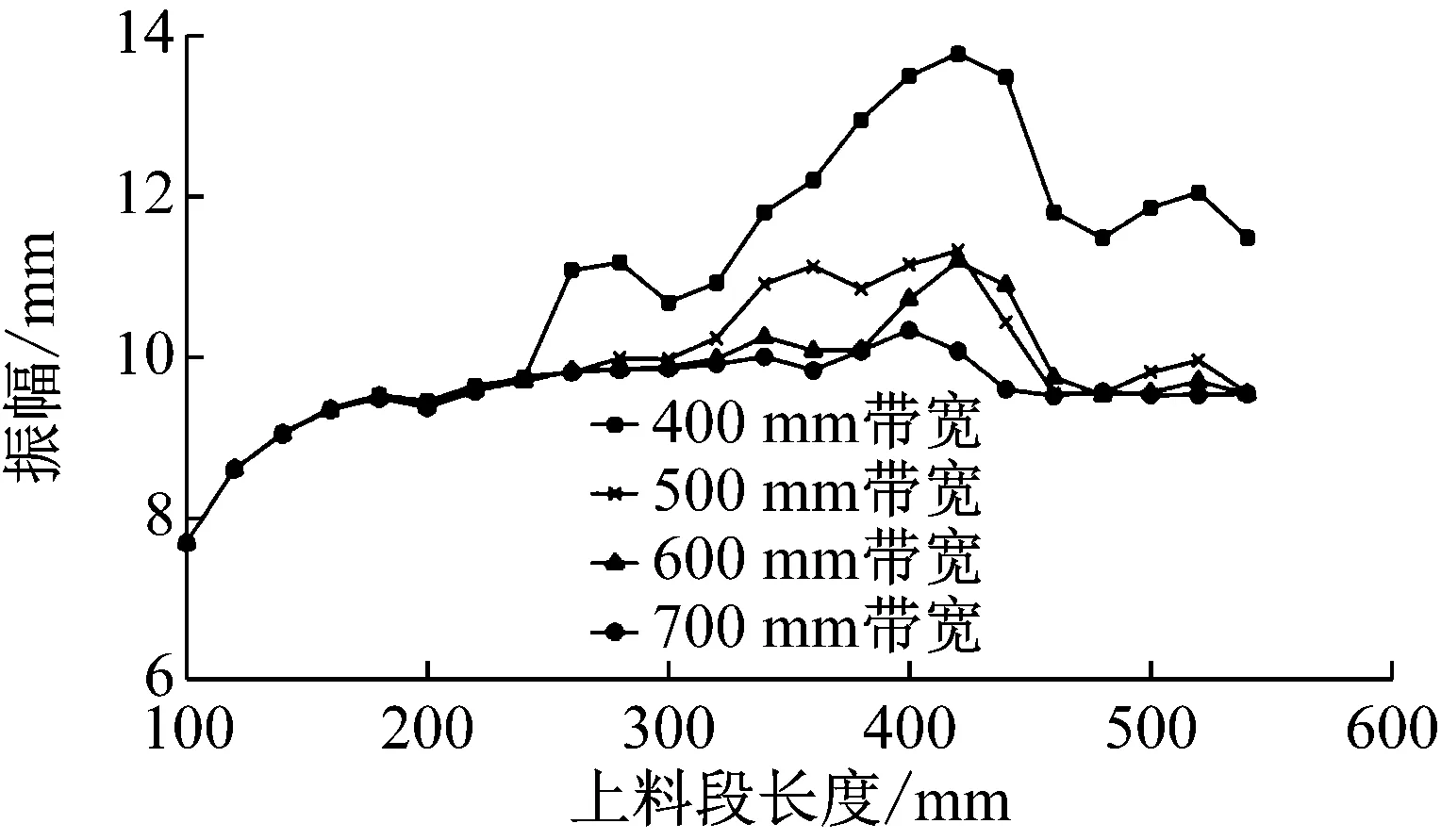
图7 输送带最大振幅上料段长度变化折线

结合图6和图7来看，上料段长度超过340 mm时，各个带宽下的反弹速度保持在0.15～0.3 m/s，600 mm和700 mm带宽下最大振幅在9.5～10 mm。综合来看，从缩短带式输送机的角度考虑，上料段长度优先选择340 mm。

3.3 带宽对反弹速度和最大振幅的影响

图8和图9反映了在3.2节中上料段长度选择340 mm的情况下，带宽对反弹速度和输送带最大振幅的影响。从图8中可知，带宽在600～1 200 mm时，反弹速度略有微涨，在小于0.3 m/s时，可根据实际需要选择大于600 mm的带宽。从图9可得，带宽超过800 mm时，输送带最大振幅基本保持10 mm不变，总体走势呈反比例函数关系。