基于干扰观测器的含风电互联电网频率稳定控制

庄 园， 徐天奇， 滕 昊， 李 琰*

(1.云南民族大学电气信息工程学院， 昆明 650504； 2.北京航空航天大学自动化科学与电气工程学院， 北京 100191)

风力发电已日渐渗入现代社会的电力系统中[1-2]，风能属于随机波动的不稳定能源，大规模的风电并入系统，必将会对系统的稳定性带来新的挑战，所以对风功率的预测技术应运而生[3]，然而对于风功率预测难以达到理想的效果，这与风本身存在随机性、不可控性等特征有关，因此将风电场输出的功率送入电网系统中存在较大的不确定量，这使得互联电网负荷频率产生波动，严重影响电网的平稳运行[4-6]。所以对于电网负荷频率的稳定控制势在必行。

负荷频率控制(load frequency control，LFC)在技术高度发达的今天已经有了一些解决方法，集中体现在控制器的设计上，较为普遍的比例积分微分(proportion intergration differentiation,PID)控制，直接连接入区域控制偏差(area control error，ACE)信号中，与电网模型构成闭环控制[7-10]，该方法简单可用，对风功率偏差有着一定的抑制效果，但也存在较大的局限性，若风功率偏差较小时，则由积分项引起的动态特性变差，而且对于微分项的难以捕捉问题，也难以解决；针对PID存在较大的控制问题，文献[11]提出模糊逻辑控制器，同样将ACE信号作为控制器的输入，通过专家系统规则库不断调整控制律，对于风功率偏差的影响可以有效跟踪并抑制，然而避免不了响应速度的较慢问题；与模糊逻辑控制器类似，神经网络启发式控制器[12-13]，作为对风功率偏差的抑制问题也是具有“高准确，低响应”的特征。

以上方法仅仅对对风功率偏差有所抑制，不能从根本上解决风功率偏差的影响，存在较大的局限性，而现代控制理论的进步，滑模控制算法以其较高的快速性在互联电网负荷频率稳定控制中得到了应用[14]，针对负荷频率波动时能够调整发电机出力，使得频率以较快的速度收敛至期望值，但其也存在一定的问题，其响应过快很容易使频率超过平衡点，并进行二次波动，同时出力较大，浪费能源，且算法本身存在抖振[15]，对于频率稳定控制有一定的局限性。Thakallapelli等[16]将自适应控制算法应用到电网负荷频率的控制中，通过不断调整未知参数，以修正频率的变化，自适应算法能取得良好的控制效果，但受到应用条件的限制，且对扰动如负荷突增敏感。Jia等[17]、曾实等[18]将飞控中经常应用的模型预测控制应用到了电网频率控制中，对ACE未来N步状态进行预测，根据未来状态值调整发电机出力，从而稳定负荷频率，该方法对风功率偏差有着较好的抵消作用，但是在线计算量巨大对于中央处理器有着较大的损伤，所以需要强大的硬件系统作为后备。文献[19]提出了事件驱动通信机制与动态输出反馈控制器相结合的控制方法，对于通信进行了优化。然而电网通信随着软件定义网络(software defined network，SDN)等技术的应用已然成熟[20]，而单使用输出反馈控制，对抵消风功率偏差以及负荷偏差等造成的影响仍然有限。

上述方法是通过提高控制系统的鲁棒性以尽量少地受风功率偏差的影响，但仍未从根本上解决风功率偏差的影响，鲁棒性稍显不足。基于以上分析，考虑到风功率偏差具备不确定性、不可控性、非周期性的特点[21]，采用观测器估计此偏差值，同时电网运行中存在负荷功率偏差、模型不确定性以及外界干扰等多源干扰环境下，可以将多源干扰视为变化率有界的集总扰动，在内层设计干扰观测器(disturbance observer，DO)对集总扰动进行估计，并反馈至控制器中进行抵消控制；再由电网控制系统的时不变特性，结合PID的优势，在外反馈环利用PID良好的控制性能设计反馈控制器并除去集总干扰项以抵消风功率偏差和负荷突增等干扰的影响，保证控制性能。所以，提出一种复合分层控制器，从根本上抵消风功率偏差以及其他干扰的影响，提高含风电互联电网负荷频率的控制性能与鲁棒性。

1 含风电互联电网建模

以典型4机双区域作为被控对象，建立模型如图1所示。

模型中，被控对象主要包括调速器、作为原动机的汽轮机、回转质量与负荷即电力系统负荷以及联络线等子模型，上下两个区域对称，在回转质量与负荷模型的输入端引入汽轮机输出ΔPti、风功率偏差ΔPw、负荷偏差ΔPl、联络线偏差ΔPtie以及不确定干扰等，输出端为负荷频率偏差Δf。由于模型结构中Δf需要经过联络线送入控制器，联络线模型不可忽略，所以可以将ACE作为输出状态量，记为y，进行控制，将控制信号输送给调速器经汽轮机更新回转质量与负荷，达到调节频率的目的。首先建立各个子模型的数学表达式。

1.1 风功率偏差模型

单一区域风功率偏差模型如图2所示。

在实际工作中风功率预测不可能准确估计风电机组的实际功率值，因此将风功率偏差作为电网的扰动输入到电力系统模型中，其值记为

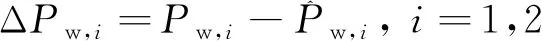
(1)

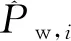
ΔPti为汽轮机输出变化功率；ΔPgi为调速器输出变化功率；ΔPtie为联络线偏差功率；ΔPw为风功率偏差；ΔPl为负荷功率偏差；Δf为负荷频率偏差；αi,βi,Ri,Tij为系统参数图1 四机双区域含风电互联电网模型Fig.1 Model of four machine two area interconnected power grid with wind power

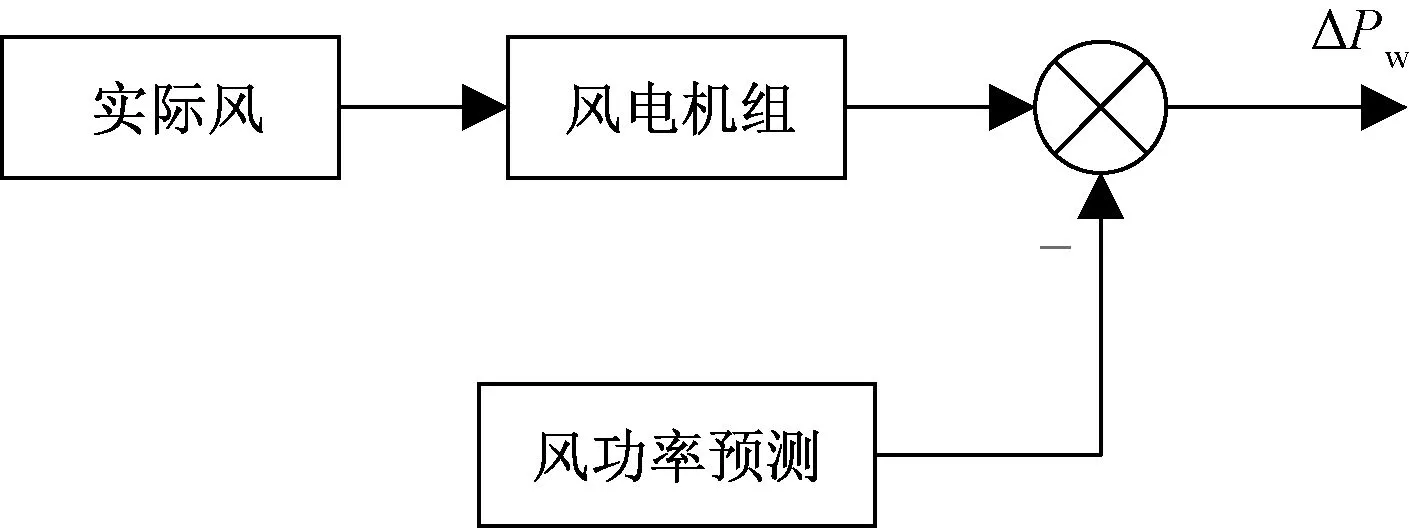
图2 风功率输出偏差Fig.2 Wind power output deviation

风功率预测按风电场出力预测时间尺度划分，包括：长期预测、中期预测、短期预测以及超短期预测，而在此，为分析方便，记风功率预测为超短期预测。另外，由于风电机组多采用桨矩角控制，跟踪最大功率输出，但由于风电场/群汇集效应和风电机组叶轮自身的转动惯性的存在，风电场/群有功输出的随机性能够在一定程度上得到平抑，因此，影响电网频率变化的风功率主要集中在中、低频范围内。

为保证研究意义及客观性，假定风为随机风，预测出的功率与实际功率偏差波动范围稍大，具体波形在仿真部分给出。

1.2 调速器模型

调速器将控制器的信号转化为速度量输入汽轮机中，其状态方程可表示为

(2)

式(2)中：Pgi为调速器输出功率；Tgi为时间常数；αi为参与系数；ui为控制输入。

1.3 汽轮机模型

由于受到汽轮机调节汽门和喷嘴之间空隙的影响，这里假定将汽门的开度值设置得较大，结合汽容现象，此部分模型可表示为

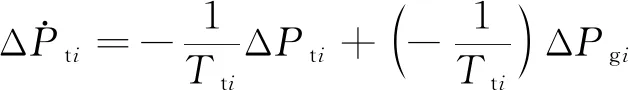
(3)

式(3)中：Pti为汽轮机功率；Tti为汽容时间常数。

1.4 回转质量与负荷模型

回转质量与负荷的模型可表示为

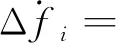
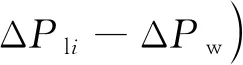
(4)

式(4)中：Di为等效阻尼系数；Hi为等效惯性系数。

1.5 联络线模型

联络线的主要任务是在扩大电网规模同时兼具优化利用各区域，实现各个区域的互联及资源的合理分配。各子区域之间的互联可通过以下方程进行描述：

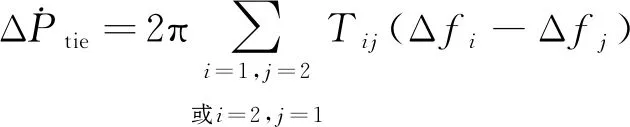
(5)

式(5)中：Tij为联络线同步系数。

综合式(1)～式(5)，针对图1区域1，令状态量x=[Δf1,ΔPtie,ΔPt1,ΔPt2,ΔPg1,ΔPg2]T，干扰量f=[ΔPl1,ΔPl2,ΔPw1,ΔPw2,T12Δf1,T21Δf2]T，则有

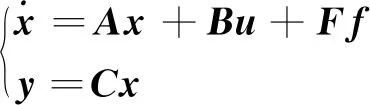
(6)

式(6)中：

为分析方便，令d=B-1Ff，则式(6)可改写为

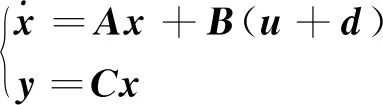
(7)

综上模型建立完毕，下面设计控制系统。

2 控制系统设计

基于干扰观测器的复合控制结构如图3所示。

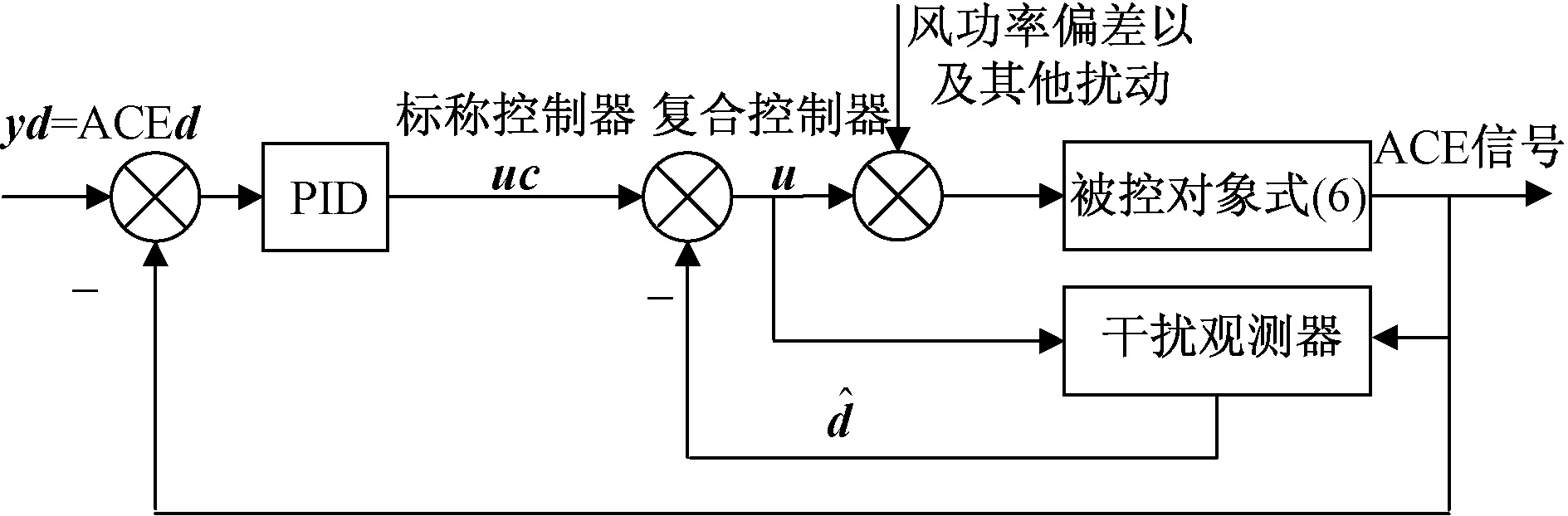
图3 基于干扰观测器的复合控制结构图Fig.3 Structure diagram of compound control based on disturbance observer

2.1 复合控制器设计

根据被控系统[式(7)]的特征,设计干扰观测器为

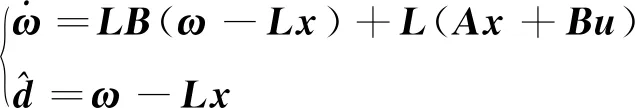
(8)

式(8)中：L为干扰观测器的增益，需要设计。

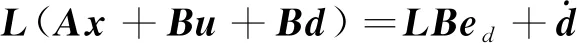
(9)

设计控制律，以抵消风功率偏差、负荷突增等其他干扰，表达式为

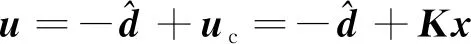
(10)

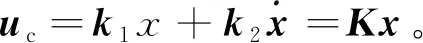
(11)

由式(11)可得看出，观测器与控制器可分层，由分离原理，可分别设计L、K，使得LB、A+BK为Huiwitz阵。

2.2 复合控制系统稳定性分析

针对式(7)被控对象，考虑一致有界收敛约束，使用线性矩阵不等式(linear matrix inequality，LMI)设计方法来计算控制器和干扰观测器的增益，首先给出定理：

定理：针对含风电互联电网负荷频率控制模型[式(7)]，对于α1>0，β1>0和β2>0，如果存在矩阵Q1>0，P2>0，且R1、Q2满足

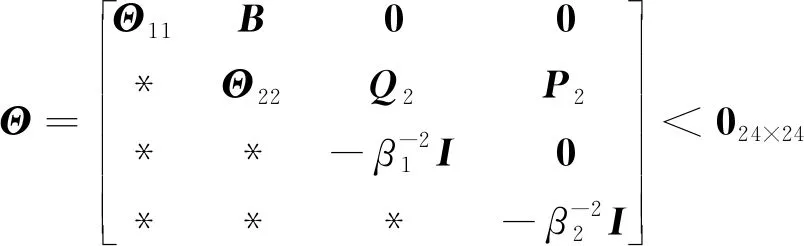
(12)

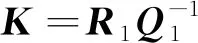
证明：

设

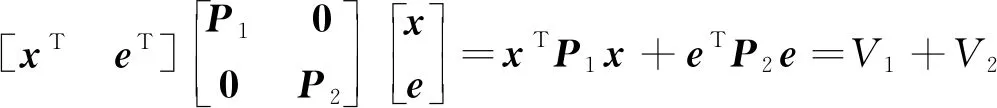
(13)

对V1求微分可得

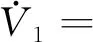
(14)

同理，V2求微分可得

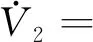
-eTsym(P2LB)e+2eTP2d≤

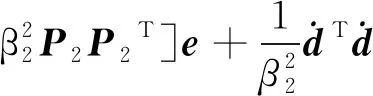
(15)

综合式(14)、式(15)可得

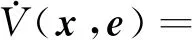
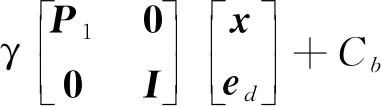
(16)

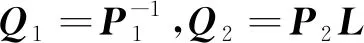
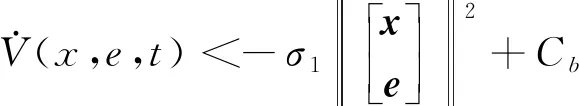
(17)

求解式(17)可得

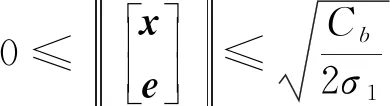
(18)

同时，可根据MATLAB计算出Q1、Q2、P2、R，进一步可得观测器参数与控制器参数分别为

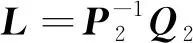
(19)

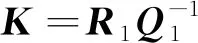
(20)

下面通过仿真验证所设计算法的可行性与先进性。

3 仿真验证

为验证文中提出的负荷控制器算法的性能，下面对4机双区域系统进行仿真，设定风渗透率为10%，系统状态初值设为0，系统模型参数如表1所示。

根据定理1，取α1=1 600、β1=1、β2=1 000，得到区域1与区域2的控制器参数分别取k11=-4.351 5、k12=-0.435 1、k21=-5.5、k22=-0.55；区域1与区域2干扰观测器增益取值L1=L2=[0.3,0.2,0.3]T。所比较的PID算法根据粒子群算法取得每一时刻的最优值。

设计风功率偏差图如图4所示。

图4中，风速用MATLAB函数产生的随机值代表随机风功率偏差。

考虑在区域1接入如图4所示风功率偏差工况，分别对区域1、2的功率偏差、ACE响应，以及联络线进行仿真得到如图5所示结果。

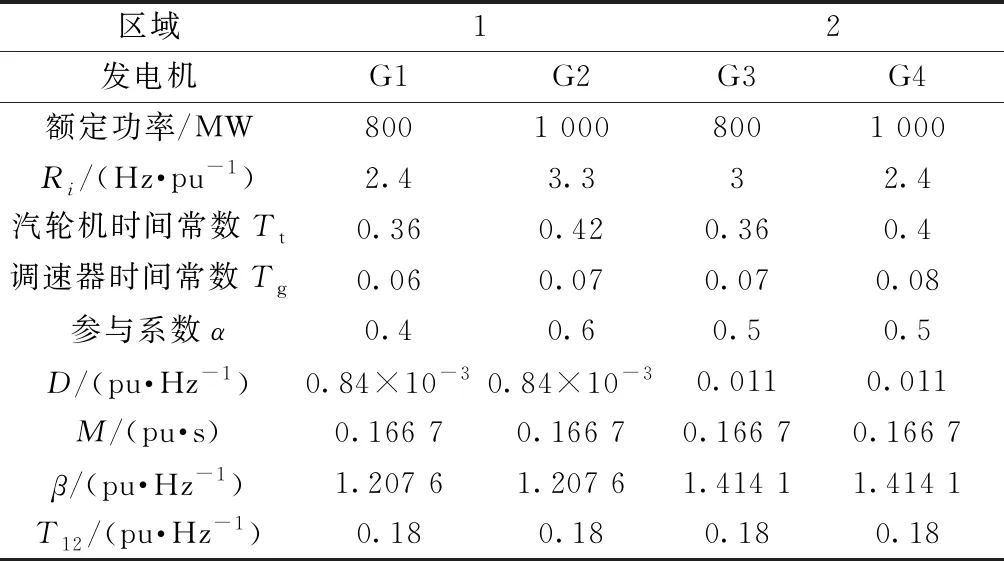
表1 系统模型参数

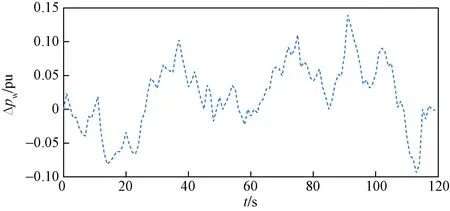
图4 风功率偏差Fig.4 Standard deviation of wind power deviation

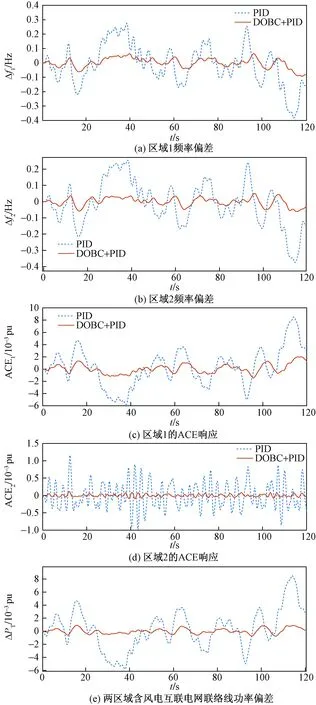
图5 双区域互联电网仅在区域1风功率存在波动时的系统响应曲线Fig.5 System response curve of two regional interconnected power grids when single region wind power fluctuates

由图5(a)可知，PID控制在区域1存在风功率偏差的情况下控制效果远不如负荷控制器的控制效果，尤其在风功率偏差波动较大的35～40 s、90～100 s以及110～120 s区间内，PID控制下的区域1频率偏差波动范围超出了电网安全稳定运行的范畴，相比之下，复合控制器可以补偿风功率偏差干扰的影响，将区域1的频率稳定在一个较小的区间内。由于互联电网的影响，区域2的频率偏差依然会受到区域1风功率偏差的影响，这从式(7)也能得到验证，同样PID控制也不能有效抑制或抵消区域1风功率偏差的影响，而所设计的复合控制算法则可以有效抵消风功率偏差的影响，如110 s处，PID控制下的频率波动较大，而复合控制器则取得了较好的控制效果。

图5(c)区域1的ACE响应在PID算法下的波动同样十分明显，特别在15、35、95、110 s附近出现了较大的波动，而所设计算法则使得ACE响应较为平缓，并保持在一个小范围内。

相较于区域1比较大的波动，对于图5(d)区域2的ACE响应来说，无论是PID还是所设计的算法，都能保证区域2的ACE响应在较小的范围内波动，且所设计的算法使得ACE响应更为稳定。

对于图5(c)中的ACE，PID算法下的ACE波动范围较大，所设计算法却能将区域控制偏差维持在较小的范围。而对于区域2的ACE来说，虽然ACE在仅区域1加风功率偏差的情况下波动范围较小，但仍能看出复合控制算法相比于PID控制方法有较强的鲁棒性。在图5(e)所示联络线的对比图中，也看到所设计算法优于PID。

上述仿真仅验证在单区域有风电接入情况，在实际中，可能同时出现风功率波动和负荷突增的情况，故需要进一步验证算法的有效性与鲁棒性。

考虑两区域同时接入风电，生成的风功率偏差如图6所示。在此工况条件下，为体现算法较强的鲁棒特性，在10 s和50 s分别在区域1和区域2处增加负荷突增阶跃干扰如图7所示。

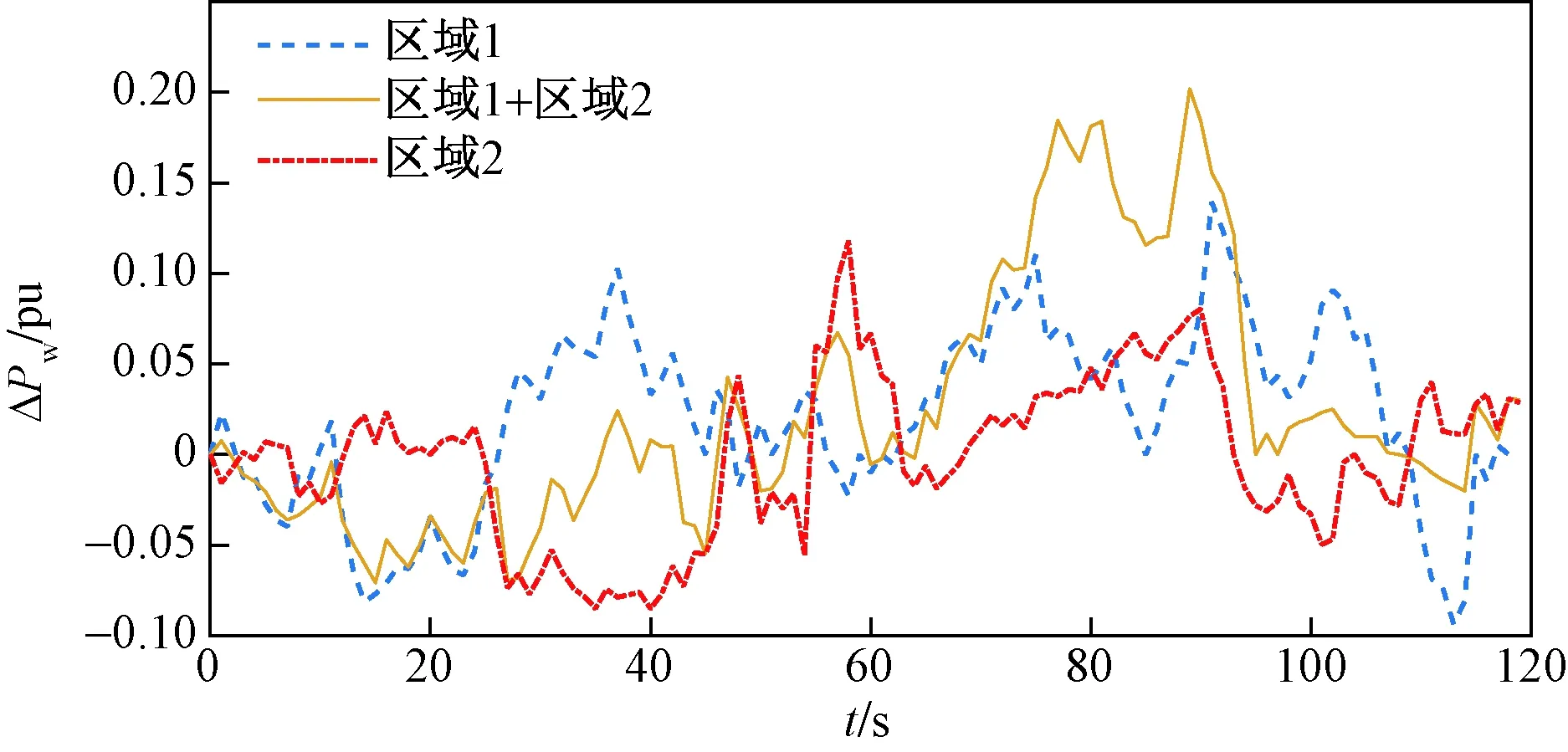
图6 双区域互联电网风功率偏差Fig.6 Standard deviation of wind power deviation between two regions

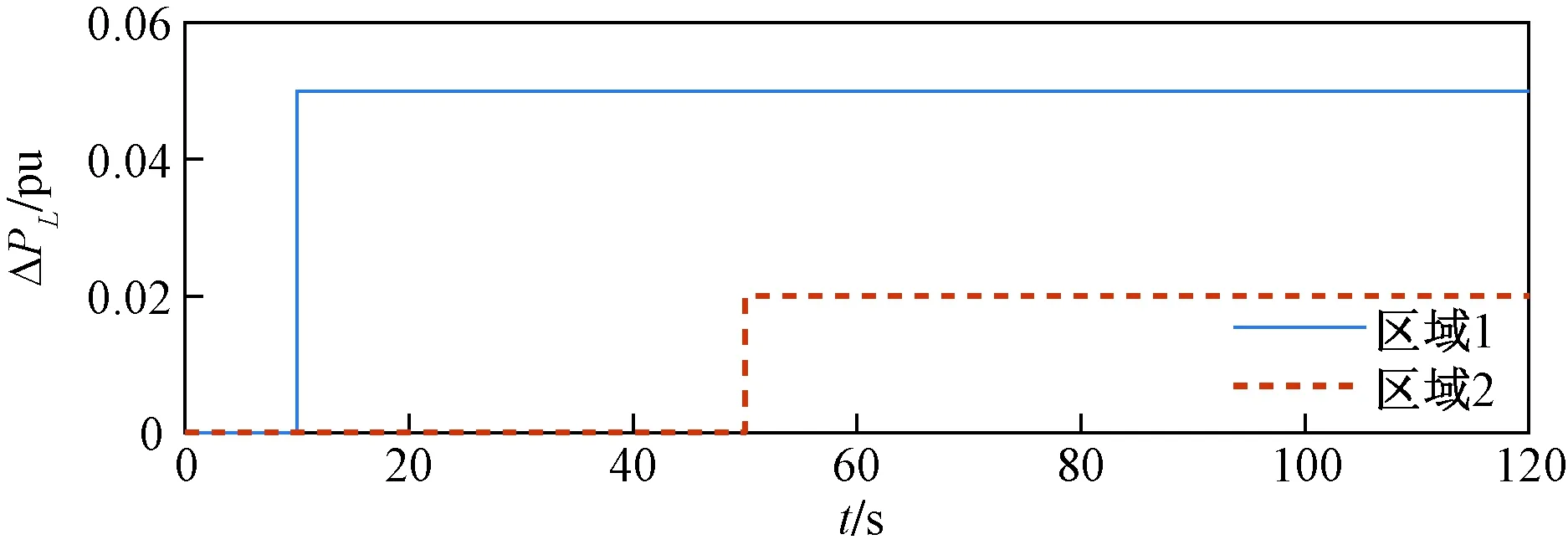
图7 阶跃响应干扰Fig.7 Step response disturbance

基于以上多源干扰情况下，对双区域进行仿真分析，如图8所示。

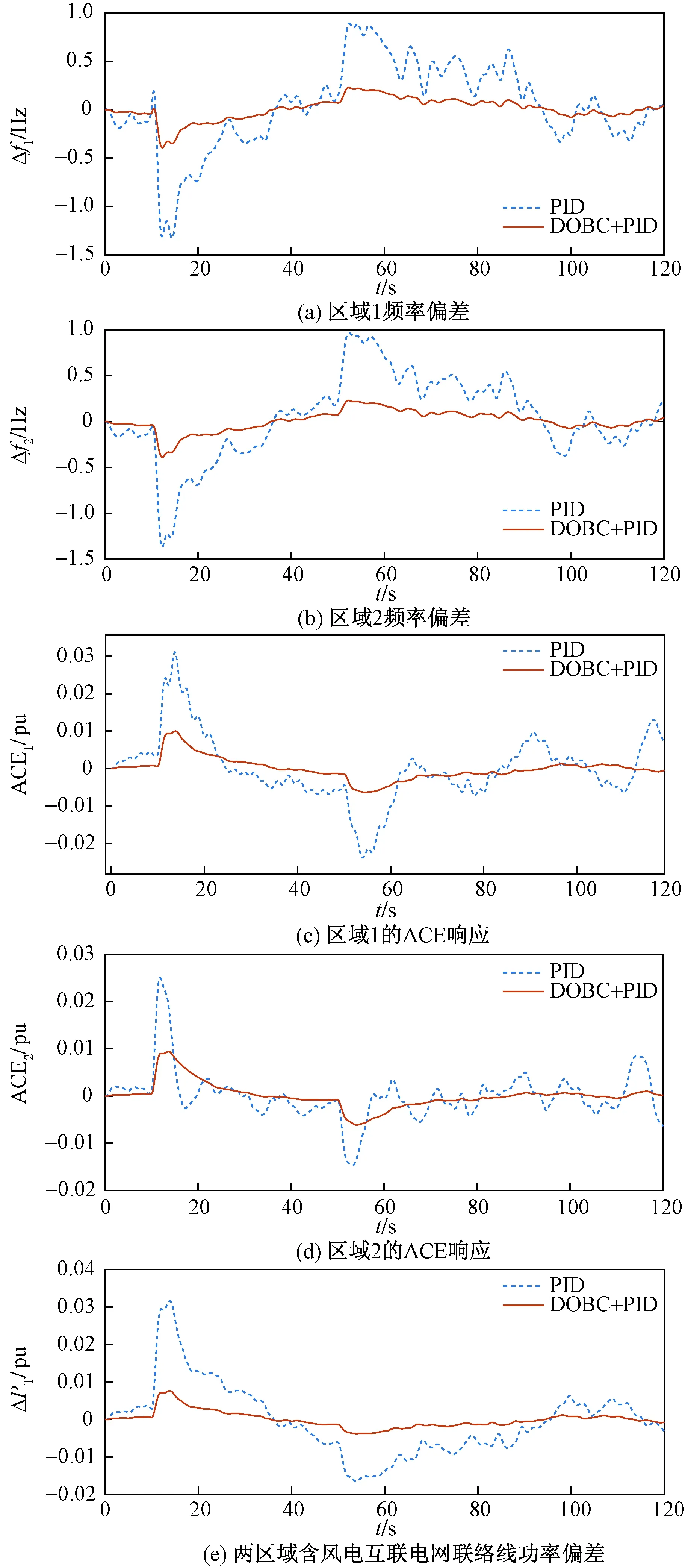
图8 两区域互联电网在风功率偏差和负荷突增同时存在时的系统响应曲线Fig.8 System response curve when the load of the two regions’ interconnected power grids increases suddenly

由图8(a)所示，在区域1中，PID方法在20～40 s频率偏差已经出现了较大的波动反应，在10 s及50 s负荷突增干扰存在的情况下，偏差误差较大，严重危害电网的稳定运行，而所设计算法在仿真时段表现稳定，效果较好，尤其在负荷突增的时刻，表现了较强的鲁棒性能，于极短时间内达到期望裕度，相比PID需要的收敛时间，有着非常大的提升；图8(b)与图8(a)类似，可以看出所设计算法明显优于现在普遍使用的PID控制。

由图8(c)和图8(d)两个区域的ACE响应来看，PID算法下的ACE波动范围较大，而所提出的复合控制算法则非常稳定，在负荷突增情况下仍然能较快收敛。在图8(e)所示联络线的对比中，也看到所设计算法明显优于PID。

由图8(c)和图8(d)两个区域的ACE响应来看，PID算法下的ACE变化十分明显，而所设计算法使得ACE响应更为平缓，除了受到区域接口量的影响外，基本可以稳定在极小的范围内。

综上，所提出的控制算法能够有效提升控制性能，增加电网频率控制的鲁棒性。为验证算法的实用性，下面对所提算法进行半物理实验验证。

4 半物理实验验证

所谓半物理实验，就是将实际被控对象中主要的影响设备以实物的方式引入回路进行实验，这样既弥补的数字仿真的虚拟性的不足，以及全物理仿真成本高的缺点。

为了验证所提出控制策略的可靠性与实用性，根据实验室条件，通过半物理仿真平台对文中提出的算法进行实际验证，实验平台如图9所示。

实验时，通过发电机2用来模拟实际发电机的作用，飞轮4能反映真实的发电机出力，实时仿真机6作为虚拟互联电网模型，通过陀螺仪8模拟产生风功率偏差，机械可变电阻器9用来模拟负荷偏差，风功率偏差值与负荷功率偏差值并通过RS422通讯传输至主控板3，实验数据通过液晶显示器5显示。

设置风电渗透率为10%，控制参数取值与第3节一致，实验时长为300 s。由于电阻器的特殊调节性，不能长时间置0，所以在85 s及180 s时刻提高电阻器9的电压，并在200 s关闭电阻器，以测试抵消负荷突增的控制效果。陀螺仪模拟的风功率偏差、电阻器模拟负荷突增与互联电网负荷频率偏差的实验结果分别如图10～图13所示。

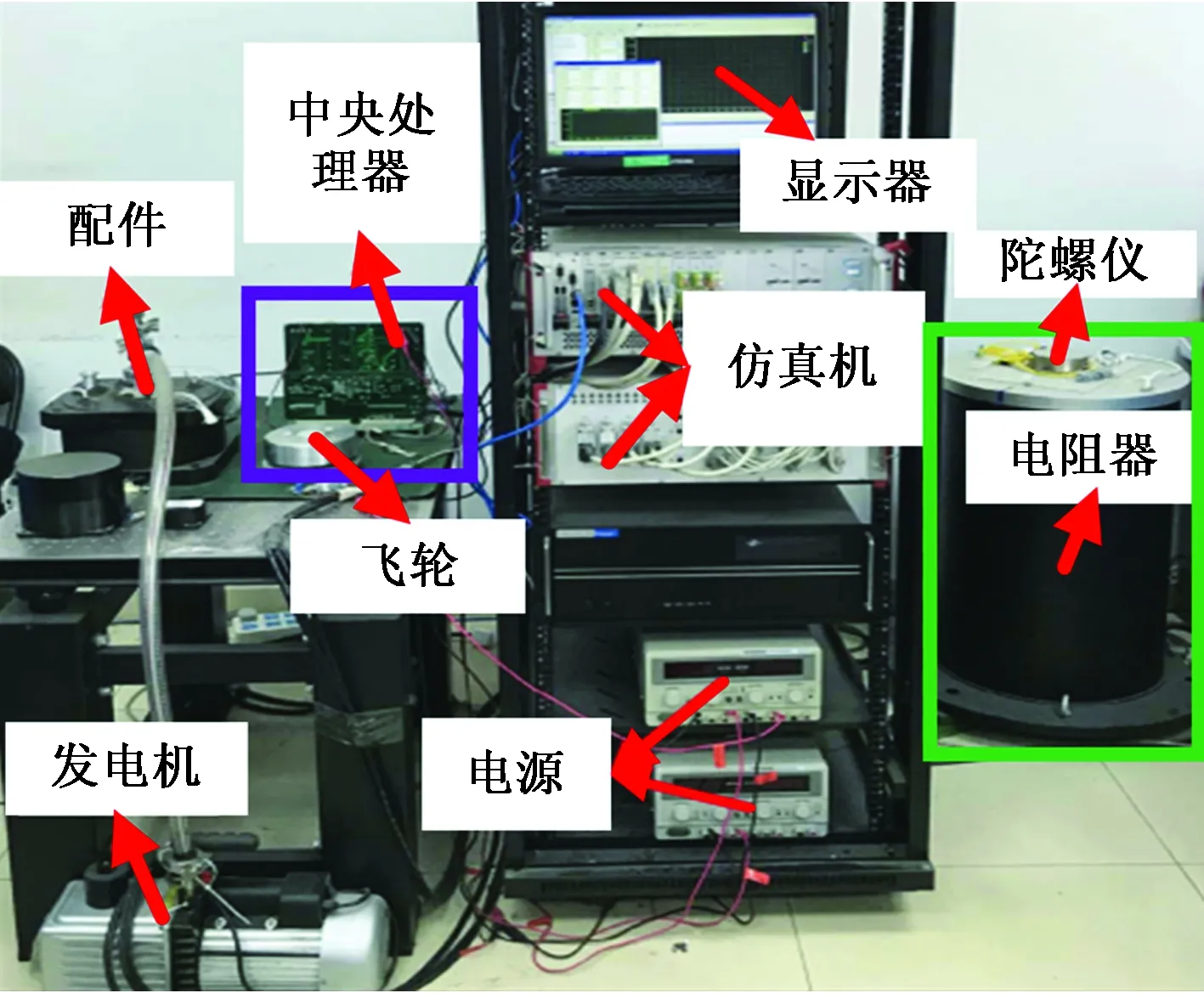
图9 含风电互联电网负荷频率控制实验平台Fig.9 Experimental platform for load frequency control of interconnected power grid with wind power

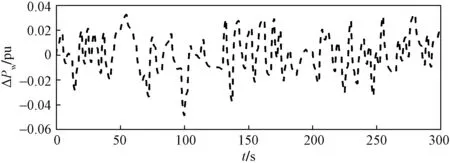
图10 陀螺仪模拟风功率偏差曲线Fig.10 Simulated wind power deviation curve of gyroscope

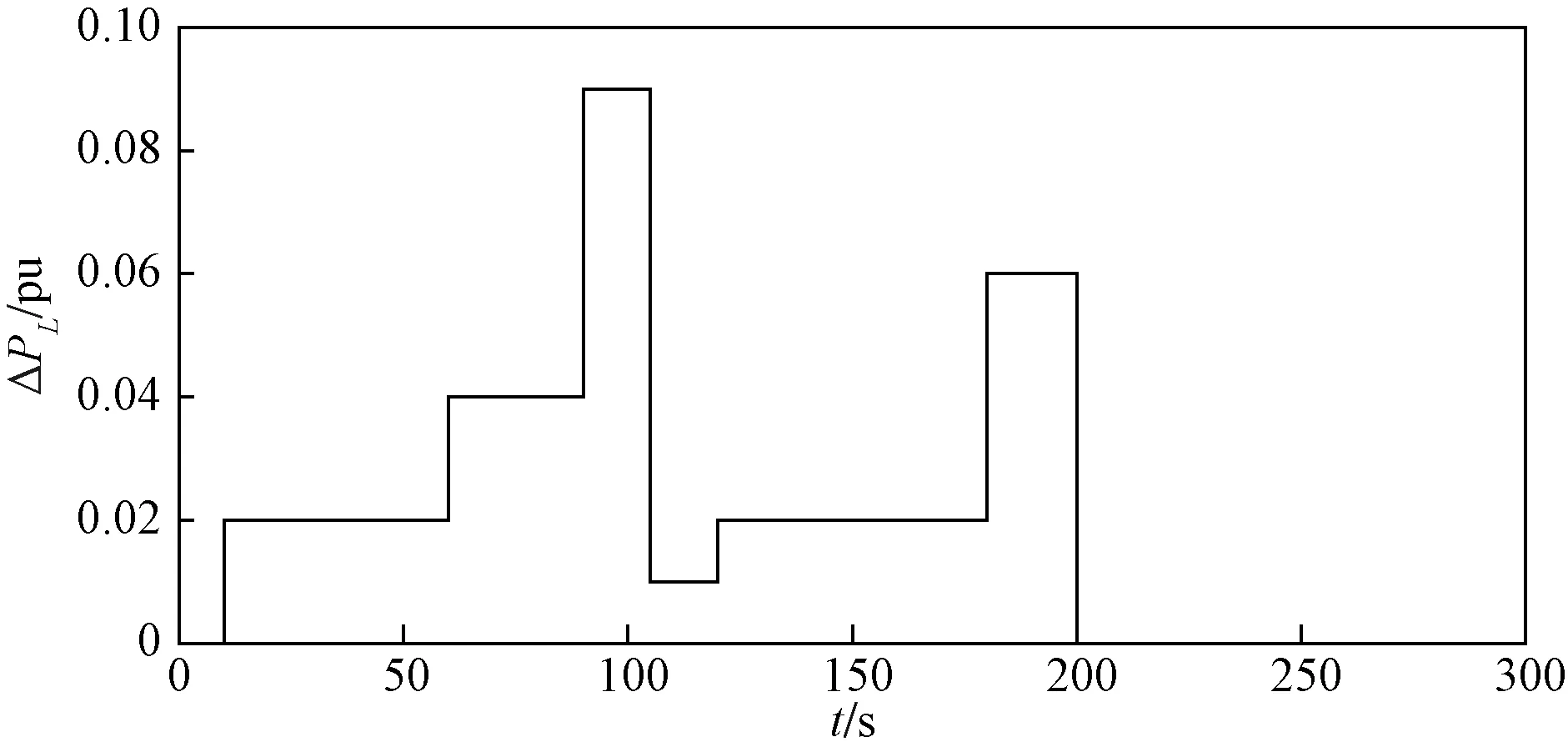
图11 电阻器模拟负荷突增曲线Fig.11 Simulated load surge curve of resistor

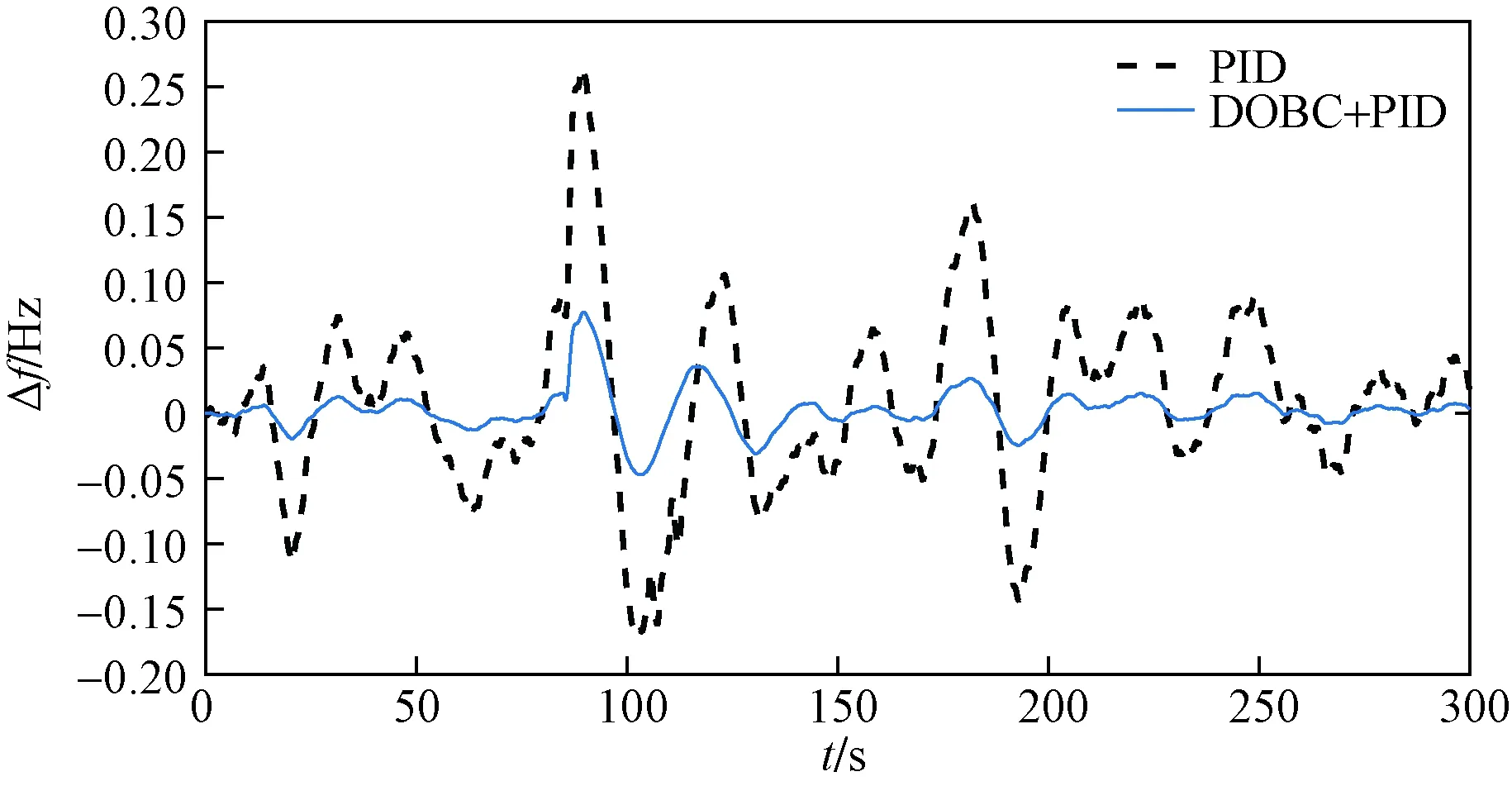
图12 负荷频率偏差曲线Fig.12 Load frequency deviation curve

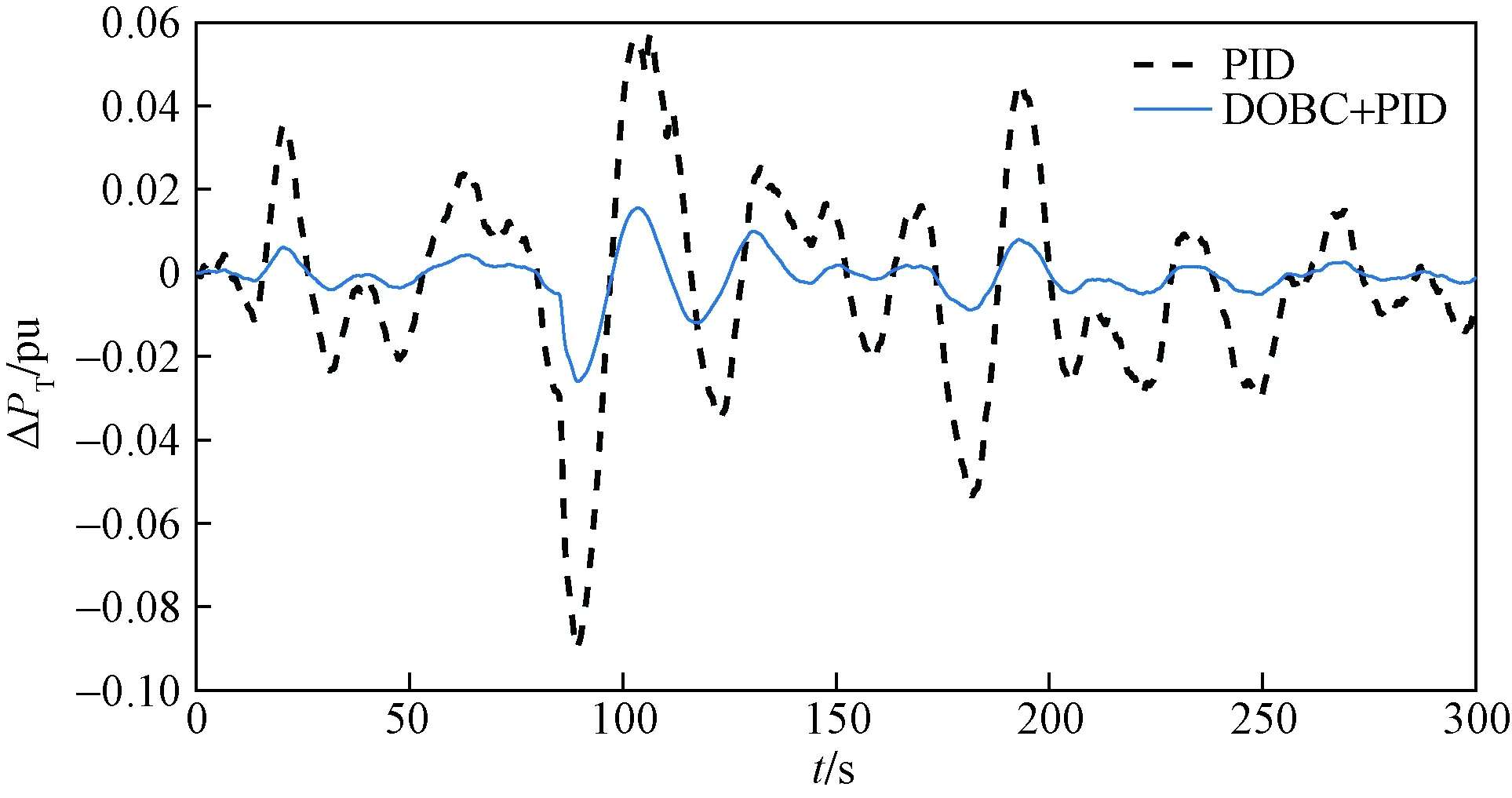
图13 联络线功率偏差实验曲线Fig.13 Power line deviation test curve of tie line

根据实验结果所示，在图10、图11的影响下，所提出的复合控制器能够较好地抵消风功率偏差的影响，尤其是在20 s、60 s、230 s、250 s时，风功率偏差较大，所提出的算法能较好地抵消风功率偏差的作用，相比于PID算法，负荷频率偏差波动更小，收敛更快；对负荷突增也有较快的响应，在85 s以及180 s的时刻能使负荷频率偏差收敛，而PID算法则出现了较大的波动。在联络线功率偏差实验曲线图中，也能明显比较出所提算法拥有较出色的性能以及较强的鲁棒性，有效减少联络线的负担。

综上，实验结果表明，所提出的控制算法能够有效抵消风功率偏差及负荷突增的影响，使得电网负荷频率偏差收敛。验证了该算法的可行性、有效性，并且具有高性能、强鲁棒性的特点。

5 结论

针对风功率偏差的影响，同时考虑负荷突增以及模型不确定性及外界干扰存在的多源干扰破坏了电网负荷频率稳定的问题。首先对电力系统进行建模，然后基于模型提出改进控制器的优化策略，针对模型的特点设计复合控制器包括干扰观测器与PID控制器以抵消风功率偏差以及负荷突增对电网负荷频率的影响。基于分离原理与线性矩阵不等式求取了观测器与控制器参数。通过仿真可得复合控制器有着出色的控制性能与鲁棒性。通过半物理实验验证，所设计算法能够有效抵消风功率偏差及其他扰动的影响，有较好的实用性，有效提升了电网频率的安全与稳定性，对电网频率控制有着较大的参考价值。

下一步的研究可以从以下两个方面进一步思考。

(1)算法的快速性，可以增加滑模控制以提高系统的快速响应能力，但应保证消除抖振影响。

(2)还可以多角度分析含风电互联电网环境、模型等“干扰”对电网负荷频率的影响，对部分干扰进行精细化表征，针对干扰模型的特点进一步设计相应的控制器。