基于压缩感知的Logistic多涡卷混沌保密通信
2021-05-07黄沄,张鹏
黄 沄,张 鹏
(1.重庆邮电大学资产管理处, 重庆 400065; 2.重庆邮电大学教务处, 重庆 400065)
混沌信号具有非周期性、类似随机噪声的宽频谱特性、良好的相关性等统计特性,因此在保密通信中有着巨大的潜在价值[1]。混沌在保密通信系统中的研究取得了一定的研究成果,如张定梅[2]提出了一种基于3个半导体环形激光器进行双路混沌通信的方案,引入交叉反馈后,混沌信号的质量得到了明显的改善,但在传输距离上对通信质量的提升有一定的制约。Zirkohi[3]提出一种基于多项式模糊模型的同步多涡桨混沌系统的安全通信设计方法,采用基于多项式-模糊模型的混沌同步方法实现了系统的自适应混沌同步,但效率不高。肖成龙等[4]运用Lyapunov指数与NIST测试验证了该混沌系统的混沌特性及随机性,提高安全性,但对信号传输性能有一定的影响。王灿妮等[5]以Logistic映射迭代的数据替换驱动系统的参数,建立一种参数调制的混沌保密通信方案,但仅局限于图像保密通信方案。刘林芳等[6]应用混沌阵子相空间对称阵子和同步,提出了基于相空间对称混沌阵子的保密通信系统,可满足其在大规模保密通信中的应用,又能保持原混沌阵子的优良特性,但复杂度比较高。
针对目前混沌保密系统存在的问题和不足[7-10],现以Logistic混沌为研究对象,从混沌信号的复杂度与传输长度角度,引入多涡卷思想,将Logistic混沌进行改进,同时引入压缩感知思想,采用Logistic混沌对信号进行长度的控制,得到的重构信号用于异步数字保密通信系统,并验证该信号保密通信处理方法的可行性。
1 压缩感知理论
假设X∈RB×1表示一维信号,信号X在一组B×B维正交基η={η1,η2,…,ηB}上展开为
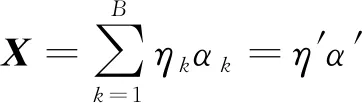
(1)
式(1)中:αk=
将信号XB×1投射到一组测量矩阵φA×B(B≪A)上,从而得到X的A个采样数据YA×1,即
Y=φX
(2)
在函数的表示上,可以将式(1)、式(2)相结合,得到采样数据Y与变换系数α之间的函数关系为
Y=φ×X=φ×η×α
(3)
根据上面的描述,压缩感知的数据采集描述如图1所示。
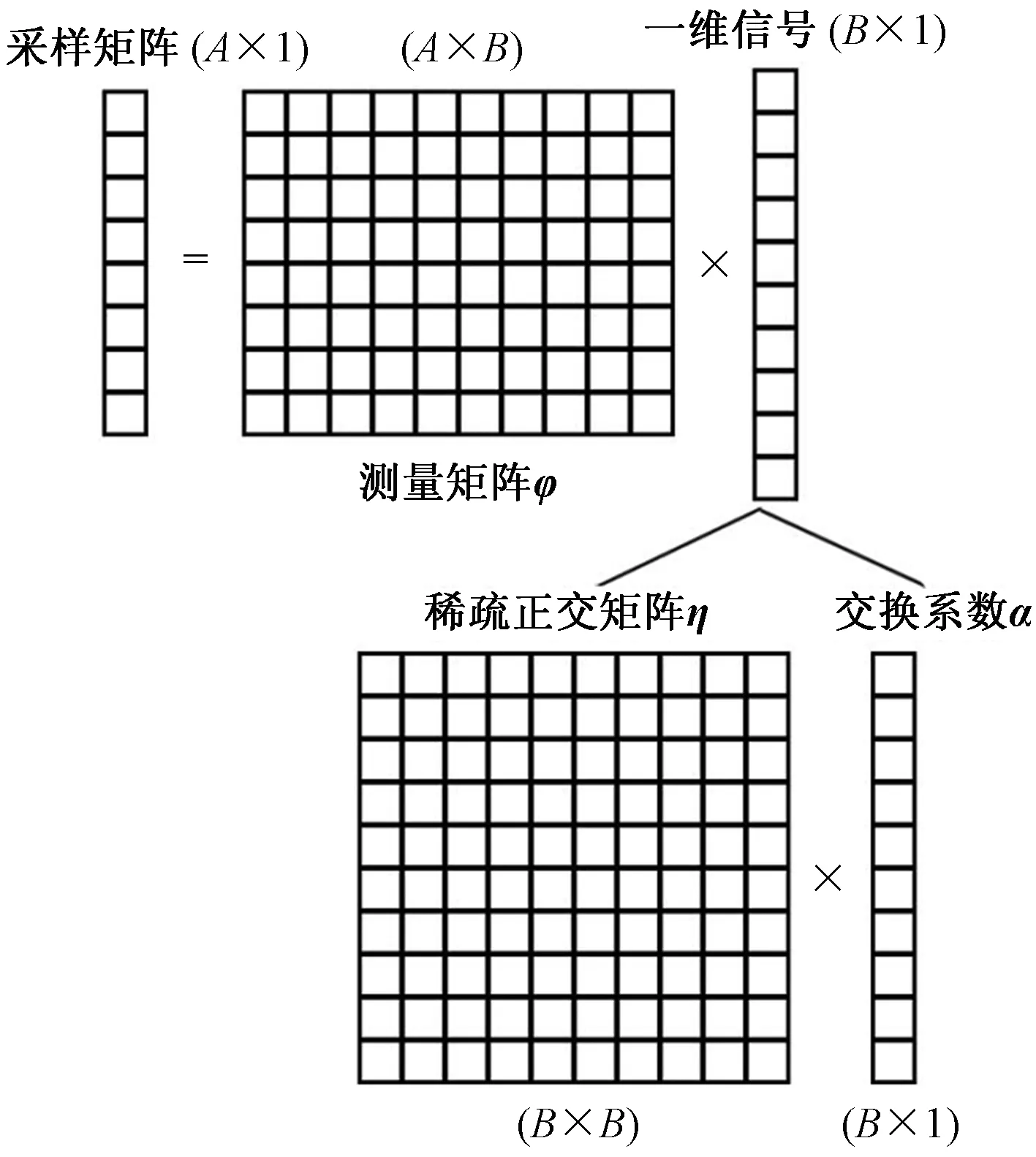
图1 压缩感知的数据采集过程Fig.1 Acquisition process of compressed sensing data
由图1可知,待测信号矩阵,假定它是一个二维矩阵(A×B),通过压缩后变为一个一维矩阵(A×1),同时需要考虑基于一维矩阵(A×1)需要还原为待测的信号矩阵(A×B),即需要保证正交稀疏基η、待测矩阵φ不相关,文献[11-12]中还进一步提到φ必须满足限制等距性(restricted isometry property, RIP)准则,即对任意含有k个值的B维向量h,β为信号的变换系数,待测矩阵φ应该满足:
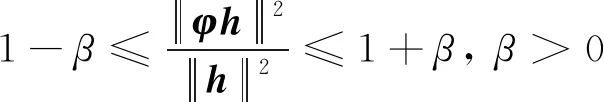
(4)
2 Logistic混沌的多涡卷改进研究
由于Tent混沌[13]与Logistic混沌[14]在信号表示上存在拓扑共轭的关系,引入多涡卷思想,Tent混沌已经可以拓展为分段Tent混沌,相应地,Logistic混沌也可以采用分段的形式,从而有助于改善其密钥空间小、序列复杂度低的问题。其中范九伦等[15]提出一种分段Logistic混沌映射方法,在试验过程中对分段映射的执行效率及信号传输的安全性进行了验证,其中,分段Logistic混沌表示为
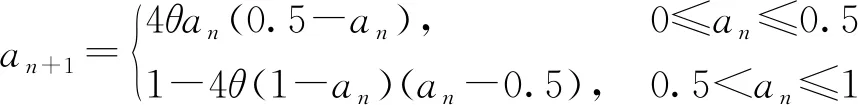
(5)
式(5)中对应的参数an∈(0,1),θ∈[0, 4],需要强调的是分段Logistic混沌具有较强的非线性性质,因为分段并不会改变该非线性函数的初始值区间、参数范围。蔡丹等[16]在范九伦研究的基础上进一步分段,提出了三段式的Logistic混沌信号处理方法,定义为
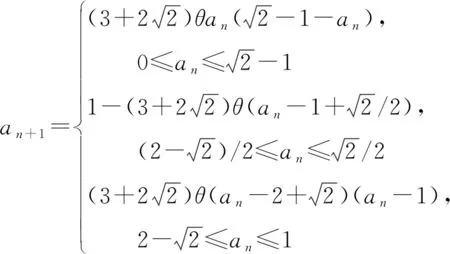
(6)
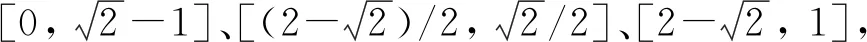
王亥等[17]进一步改进Logistic混沌,但是这个改进并不是分段,混沌函数定义为
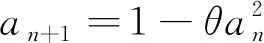
(7)
该函数在表示上与一般Logistic混沌函数相同,但是在参数的取值上有明显的改进,其中an的取值范围为[-1, 1],同时将θ的取值范围缩减为[0, 2],但是整体映射空间与原有Logistic混沌映射一致。
范九伦在王亥算法基础上进一步引入多涡卷的思想,将Logistic混沌进行分段[18],通过试验仿真证明该分段Logistic混沌的各项性能均好于一般Logistic混沌,张薇等[19]在研究扩频通信领域的通信保密性问题时,也引用了该方法,该算法的函数为
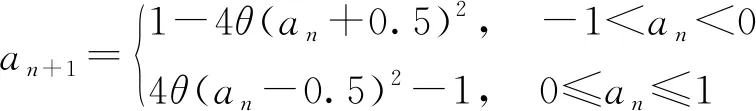
(8)
式(8)中继承了王亥算法的优点[17],即将an的取值范围设置为[-1, 1],将θ的取值范围调整为[0, 2],同时引入了分段的方法,但是算法在实现过程中适当增加了复杂度,保证了加密运算的安全性。现从Logistic混沌的安全性角度,引入范九伦等提出的两段式Logistic混沌数据处理算法[18]。
3 基于Logistic的改进混沌-伯努利测量矩阵算法
混沌是非线性系统所独有且一直都存在的一种非周期运动形式,因为混沌系统产生的数据集具有确定性、随机性等特点,因而在非线性关系、信号调制、保密通信等领域都具有较好的应用。
结合王亥等提出的Logistic混沌模型,在θ取值范围调整设置为[1.872, 2]内,a0的取值设置为0.23、0.36或者0.68时,对应的Lyapunov指数均大于0,由Logistic系统产生的随机序列{an}经过式(9)符号函数映射成序列{gn},其中:
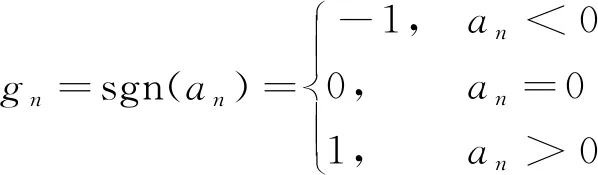
(9)
在文献[20]中提到将θ设置为2.0时,当前的Logistic系统产生的{gn}满足伯努利(Bernoulli)分布,同时也满足RIP性质,此时经由Logistic系统产生的序列{gn}可以作为压缩感知的测量矩阵。首先对Logistic混沌进行二段式处理,使其复杂度提高,整体映射空间与原有Logistic混沌映射一致,具体构造测量矩阵算法步骤如下。
(1)经过反复试验对比,证实在θ设置为2.0,a0的初值设置为0.23、0.36或者0.68时,重构后的均方误差(MSE)分别为0.096 57、0.083 15及0.088 71,取值略微存在差异,故将对应参数设置为θ=2.0,a0=0.36,通过改进Logistic混沌系统产生的混沌序列{gn},对应序列长度为n=A×B-1。
(2)将步骤1生成的序列{an}通过式(9)得到符号函数映射序列{gn}。
(3)对生成的序列{gn}进行长度为B的截取,从而得到A×B维的测量矩阵φ。根据文献[21]分析,传统的Logistic混沌算法的时间复杂度超过O(B2),而本文模型对应的时间复杂度为O(A×B),其中A≪B,通过仿真可以对本文改进混沌-伯努利(Chaos-Bernoulli)算法得到的序列与常规伯努利随机序列进行对比,如图2所示。
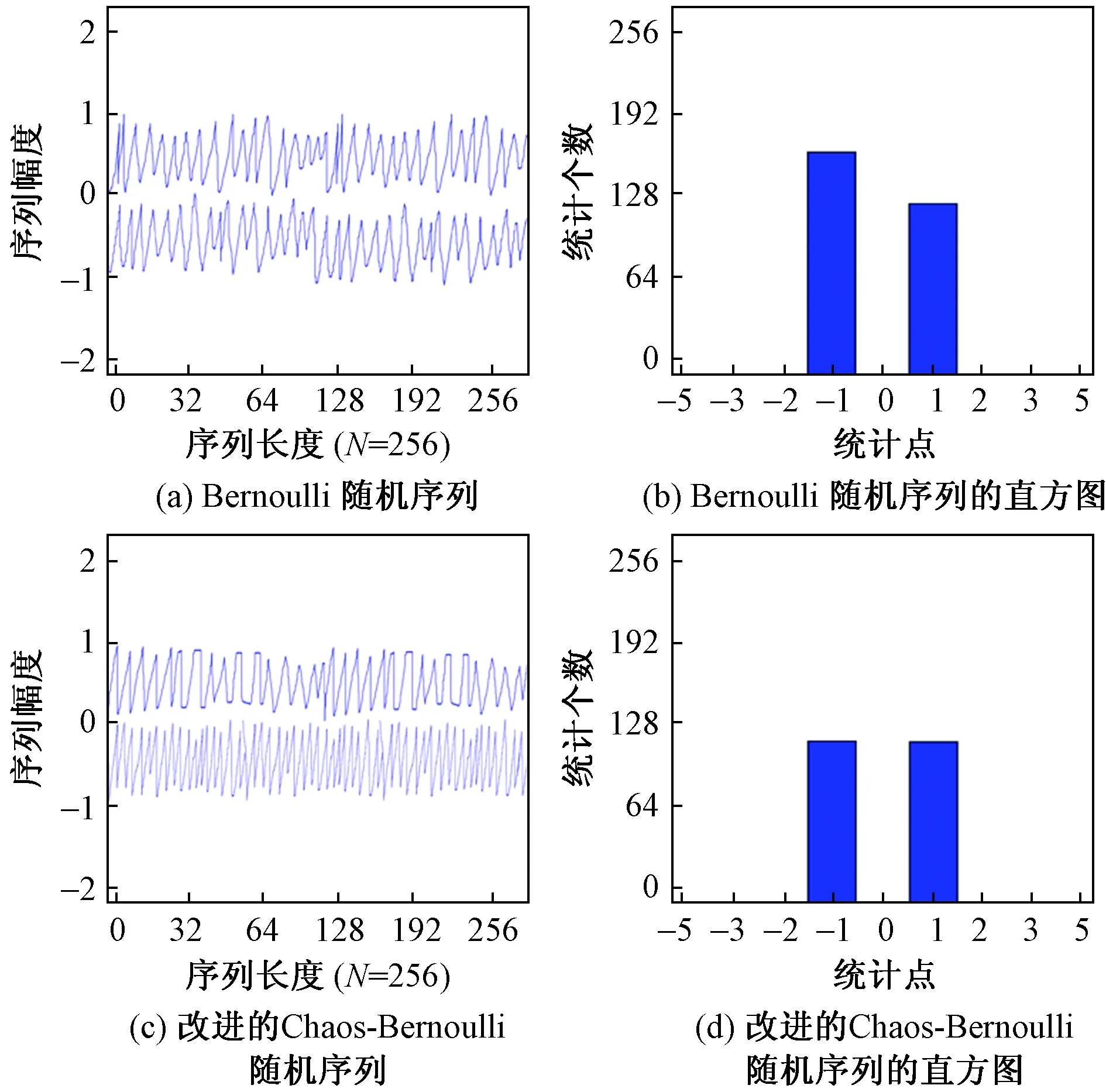
图2 伯努利随机序列与改进混沌-伯努利序列对比Fig.2 Comparison of Bernoulli random sequences with improved Chaos-Bernoulli series
在图2中对比采用混沌-伯努利生成的随机序列、伯努利生成的随机序列,会发现前者产生的随机序列具有更好地平均性、稳定性,在对应统计点-1、1的个数趋近于相同。
4 实验仿真与分析
以Logistic混沌作为研究对象,分别从信号的保密性和长度角度,引入了多涡卷、压缩感知思想,从而生成改进型混沌-伯努利测量矩阵。首先对通过一维信号进行仿真,从而验证测量矩阵抗干扰特性,然后将该矩阵信号用于异步数字保密通信系统中,验证信号的还原性及安全性。
4.1 一维信号的仿真试验
选取长度B=256的一维信号,测量数A为B的一半,即压缩比A/B=1/2,信号重构借鉴正交匹配追踪(orthogonal matching pursuit, OMP)算法,测试结果如图3所示。
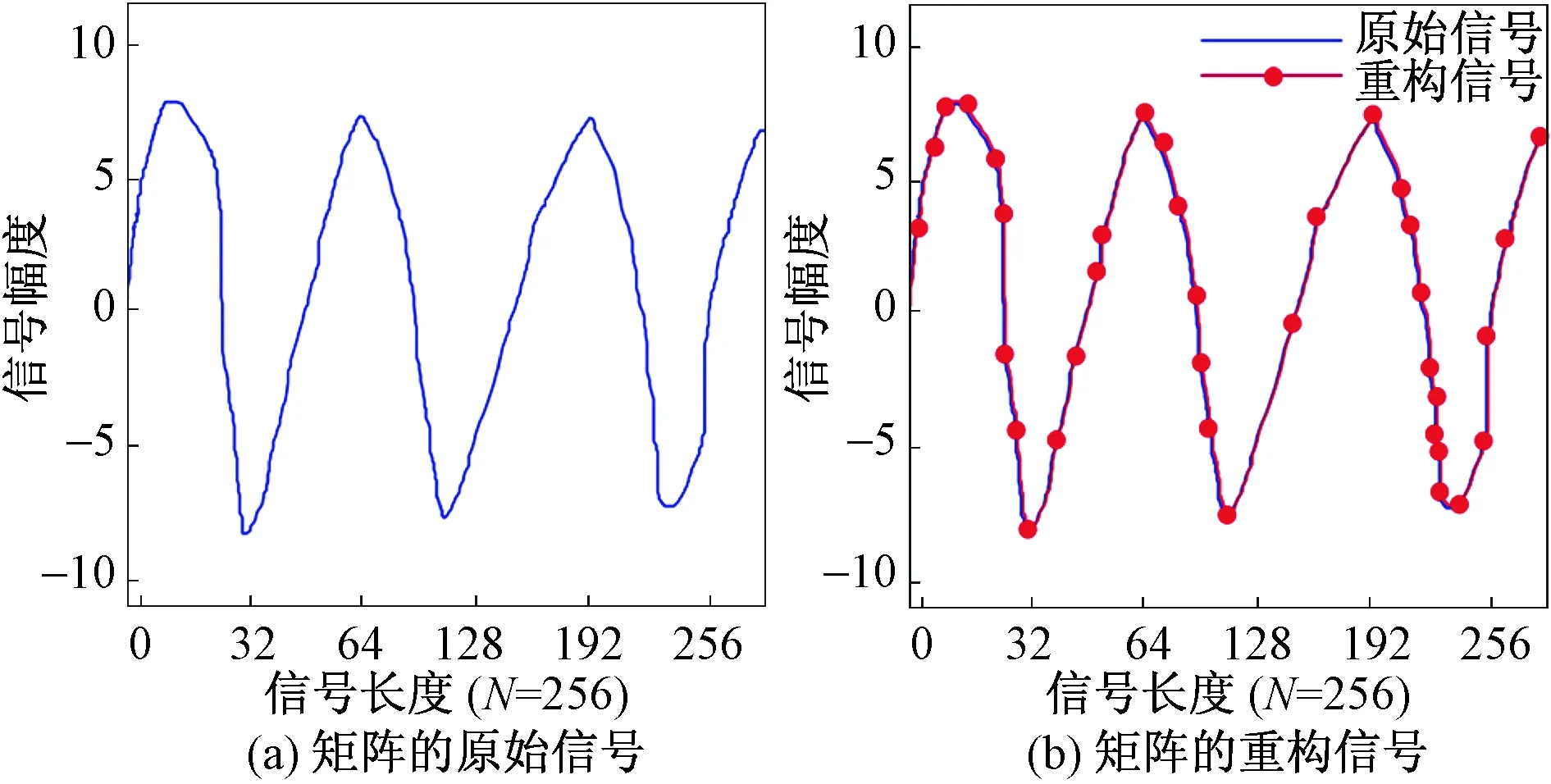
图3 一维信号的改进混沌-伯努利测量矩阵的重构结果 Fig.3 Reconstruction results of one-dimensional signal measurement matrix based Improved Chaos-Bernoull
由图3可知,采用的改进混沌-伯努利测量矩阵可以对原始信号进行重构,重构信号波形与原有的波形几乎一致。在信号长度为B=256,同时测量数A=128的情况下,即压缩比A/B=1/2时,重构信号波形与原有的波形几乎一致;当信号长度B和测量数A取不同值时测试各个测量矩阵的峰值信噪比(peak signal to noise ratio, PSNR),如图4所示。

图4 一维信号在不同测量矩阵下的PSNR对比Fig.4 PSNR comparison of one-dimensional signals under different measurement matrices
由图4可知,采用改进混沌-伯努利测量矩阵所得到的波形表现较为平稳,即伴随着压缩比的不断提高,对应的PSNR也稳步上升,同时PSNR值均优于其他测量矩阵。
4.2 异步数字保密通信系统的设计
假设p(s)是原始二进制信号序列,对每个比特进行预处理,经由式(10)得到对应的p′(s),函数表达式为
p′(s)=p(s)-{[p(s)+1]mod2}
(10)
经由式(8)可以得到A(t),其中含有a1(t)、a2(t)、a3(t)及a4(t)共4个状态变量,它们的值对应的区间不同,按照一定比例将状态变量A(t)的振幅调整到同一个区间范围内[Amin,Amax],即B(t),通过式(11)可以将a1(t)、a2(t)、a3(t)及a4(t)转换为b1(t)、b2(t)、b3(t)及b4(t)转换公式为
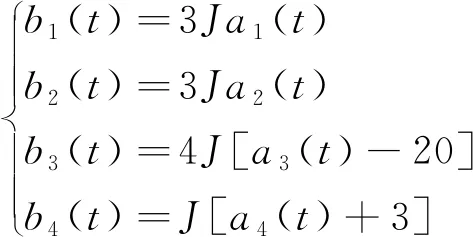
(11)
式(11)中:J为信号增益的倍数。
在B(t)中需要进行阈值的监测,即从B(t)内剔除部分在[-u,u]内的值,从而得到BC(t),其中u(u≥6)表示噪声系数,同时将BC(t)对应时刻的差值区间定义为[A,E],需要强调这里A表示的仅仅是BC(t)对应时刻的最小值,其中A=Amin-Amax,E=Amax-Amin,同时将[A,E]划分为4个子区间,分别为[A,B)、[B,C)、[C,D)及[D,E]。
对于p′(s)中每一个连续比特p′(2i-1)、p′(2i),由ni∈N决定从BC(t)的4个状态变量中选择其中bni(t)∈BC(t),取其中ci+2个连续变量值,对每个变量序列的最后两个值进行修改,从而得到b(t),如图5所示。
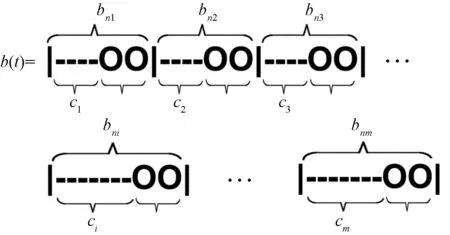
图5 b(t)的组成Fig.5 The composition of b(t)
在图5中,对于每一个选中的状态变量bni(i),其中有限个不变状态用连接符“-”代替,其中长度ci∈Ck,其中两个连续的符号“○”表示已修改的变量值,将其用于掩盖p′(s)中两个连续比特p′(2i-1)、p′(2i),因而b(4)是经由4个状态变量混合而成的序列。假定ti=[2(i-1)+1+sum(C[1∶i])]×Tb,其中i=(1,2,3,…,n)/2,k=Tb。Tb表示两个连续发射信号之间的时间间距。
对于任意b(ti),b(ti+k)∈b(t),如果|b(ti)|-|b(ti+k)|∈[-L,L],则需要调整其值使得|b(ti)|-|b(ti+k)|不在[-L,L]的范围内,否则在接收端信号无法正常恢复,通过式(12),实现从b(t)转化为b′(t),在该公式里需要根据[A,E]的4个子区间进行转换,转换公式为
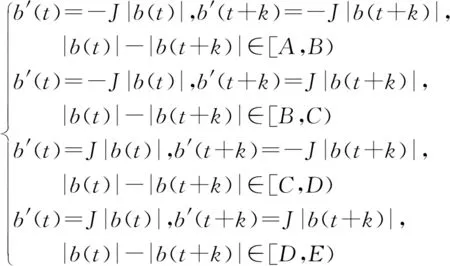
(12)
e(t)=p′(s)b′(t)
(13)
假定t=t0时刻,应用式(13),可以掩盖信号p′(s)、状态变量信号b′(t),其中b′(t)、ci以及e(t)之间的关系如图6所示,经过处理后,e(t)成为加载有意义信号的混沌信号,但是此时只能在无噪声的物理信道中传输。
考虑到物理信道肯定有噪声干扰,因而添加高斯噪声r(t)到e(t)中模拟信道噪声,从而实际发送信号e′(t)表示为
e′(t)=e(t)+r(t)
(14)
经由上述的分析,本研究搭建的异步保密通信系统,涉及状态变量的转换[b(t)]、时钟信号的变换[p(s)]以及输出信号[e(t)]的计算等,整个模型如图7所示。
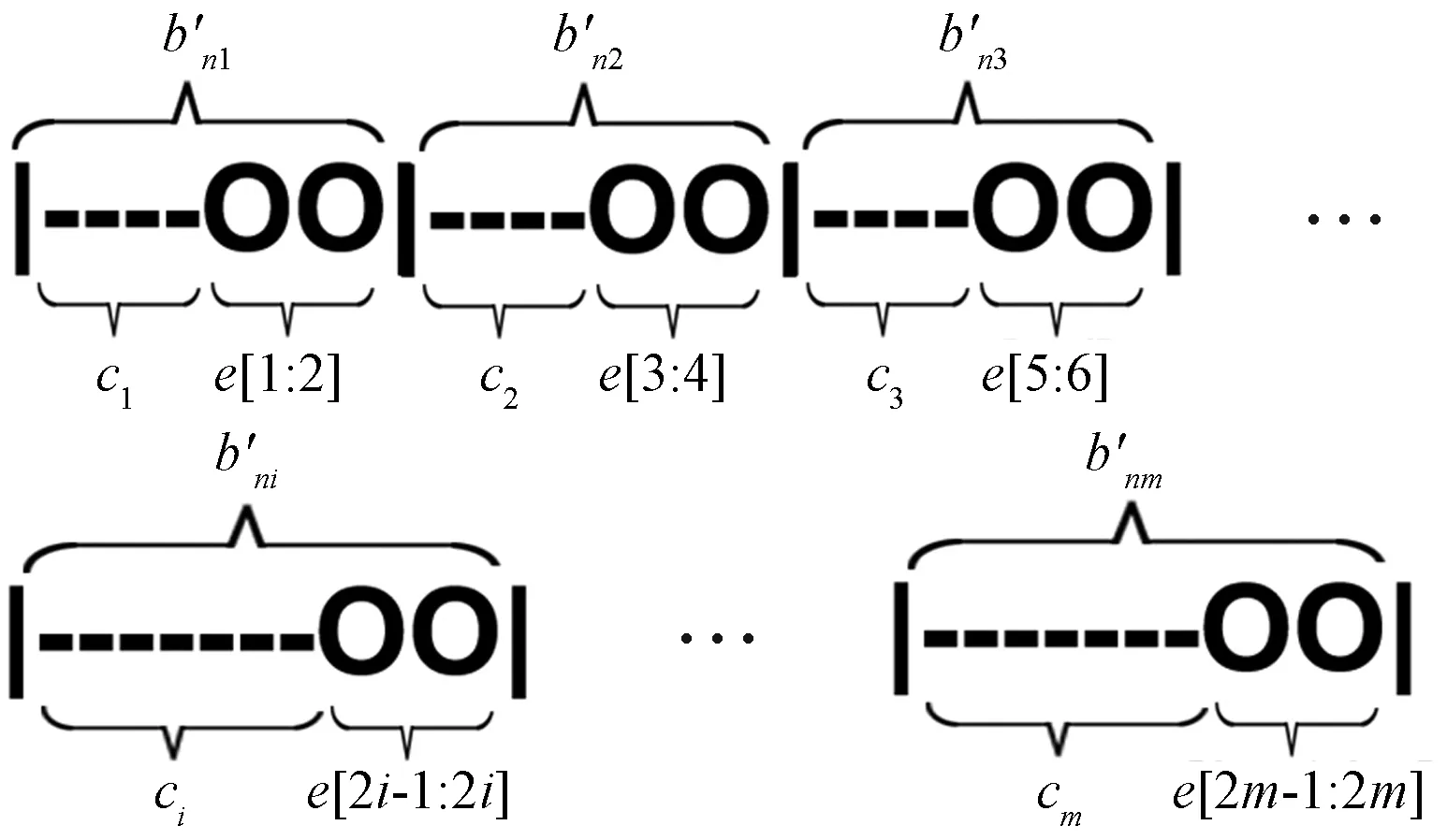
图6 b′(t)、ci以及e(t)之间的关系Fig.6 The relationship among b′(t),ci and e(t)

图7 异步保密通信系统的发送端信号调制流程Fig.7 The process of signal modulation at the sending end of an asynchronous secure communication system
由图7可知,存在3个过程:首先,状态信号变量的调制,从改进Logistic混沌矩阵获取信号后经由信号放大,明显噪声信号的剔除;其次,通过随机选取得到b(t+k),经过信号调制得到b′(t),同时设置一个时钟信号p(s)用于确定状态变量的类型;最后,将上述信号进行混合得到e(t),再添加一定噪声得到e′(t)。
异步通信系统接收端,需要对信号进行解调,即接收信号e′(t)后,通过延时得到e′(t+k),其中t∈(2QTb, (2Q+1)Tb),Q=0, 1, 2, 3,…,同时k=Tb。假定|e′(t)|-|e′(t+k)|在BC(t)对应时刻值区间[A,B)内,且e′(t)<0,e′(t+k)<0,通过式(12)、式(13)可以得到p″(s)=11,具体的信号解调计算方法如图8所示。

图8 异步保密通信系统的接收端信号解调方法Fig.8 The receiving end signal demodulation method of asynchronous secure communication system
由图8可知,信号解调根据不同的状态值域[A,B)、[B,C)、[C,D)及[D,E]可以分为4类,不同类别根据算式e’(t)、e’(t+k)的值域可以进一步划分为16种子信号值。
4.3 基于改进Logistic混沌信号的安全性模拟分析
在状态变量BC(t)的区间内,设置信号增益J=2,噪声系数L=6,采用基于改进Logistic混沌得到的3组测试值用于该异步保密通信系统,对应的误比特率/信噪比(bit error rate/signal noise ratio, BER/SNR)关系如图9所示。
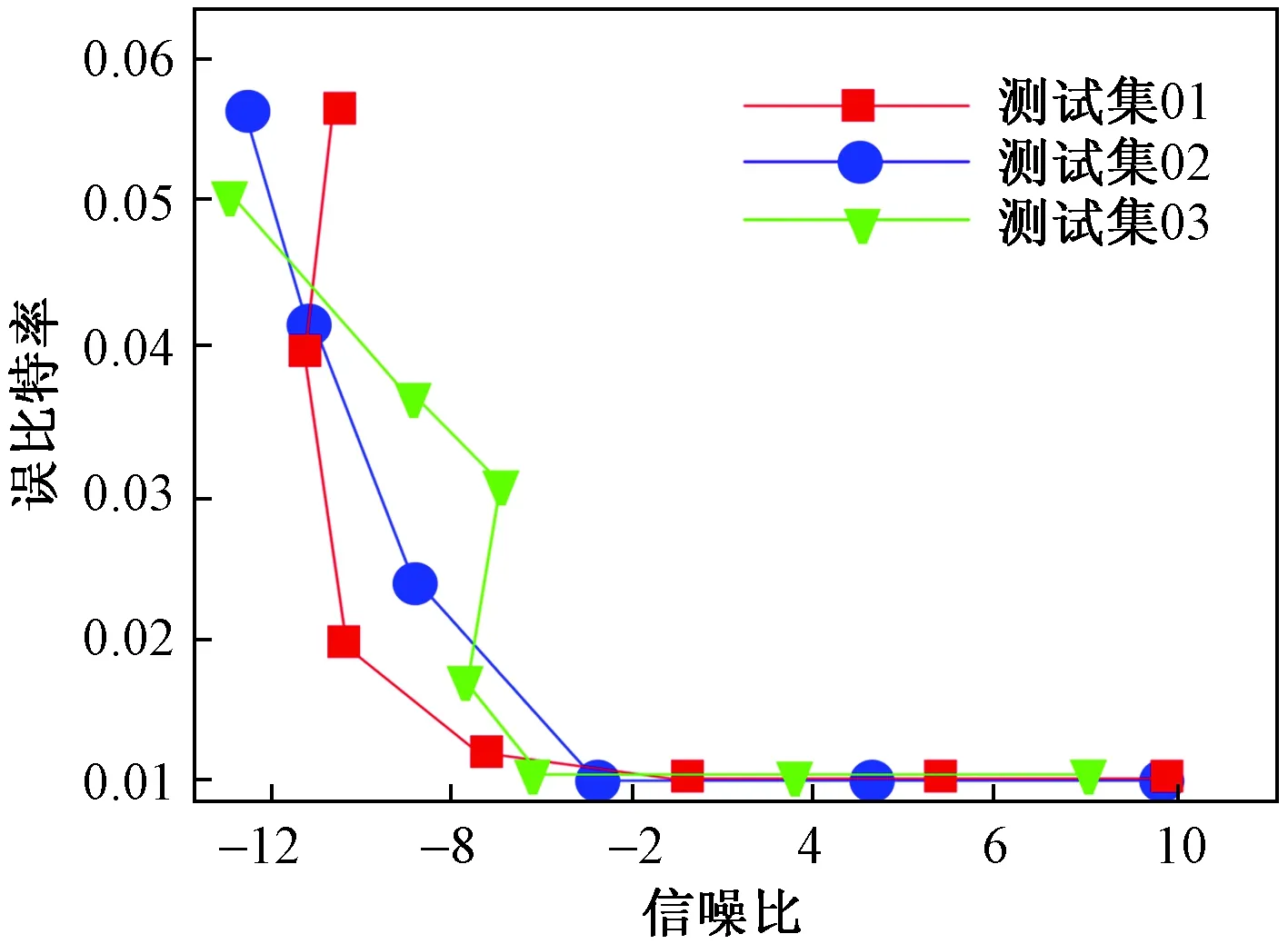
图9 在保密通信系统中SNR-BER之间的关系Fig.9 The relationship between SNR and BER in secure communication systems
由图9可知,伴随着信噪比的提高,误比特率明显下降,当信噪比提高至4及以上,对应的误比特率会进一步下降至0,即增加信噪比,数字信号可以从混沌信号中恢复。
对于定义的4种不同区间的状态变量A(t),首先需要将其调整在同一个区间内,剔除部分噪声系数在[-u,u](u≥6)内的值,从而得到BC(t),否则该区间的值会被高斯噪声掩盖,会导致解调时发生比特错误,其中,BC(t)对应b1(t)、b2(t)、b3(t)及b4(t)对应时间变换的曲线如图10所示。
假定原始信号p(s)的长度为270,通过混沌得到的信号b′(t)如图11(a)所示,该信号是由式(8)得到不同状态调整后的结果,可以看出信号还是混沌的,通过原始信号、混沌信号合并输出得到的e(t)以及加了高斯噪声的e′(t)也是混沌的信号,如图11(b)所示。
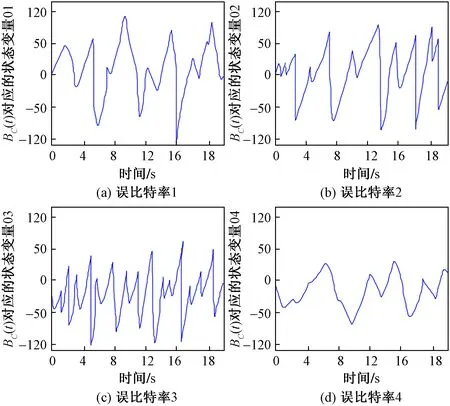
图10 BC(t)中不同时刻的状态变量值Fig.10 The values of the state variables at different time in BC(t)
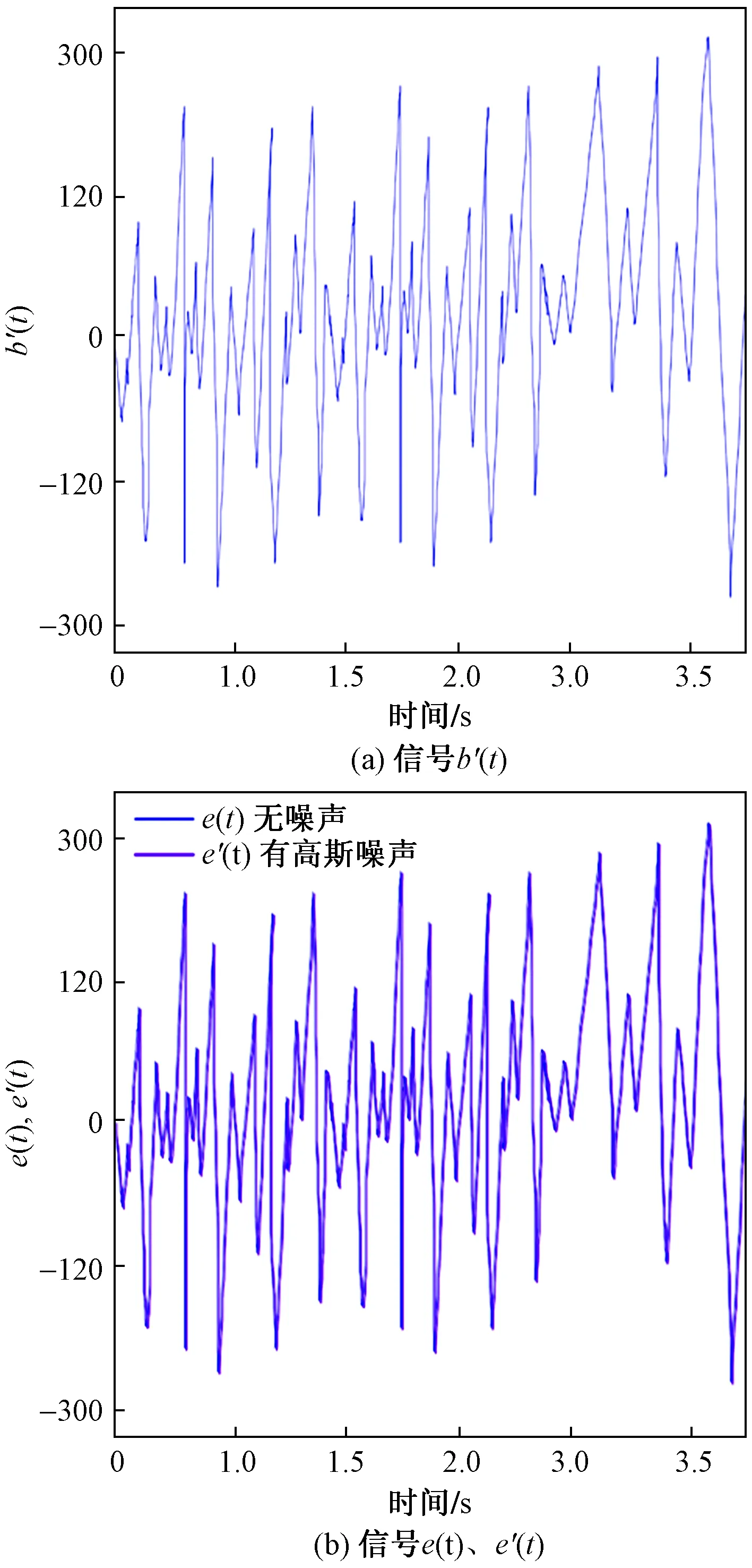
图11 混沌信号中的b′(t)、e(t)以及e′(t)Fig.11 b′(t),e(t) and e′(t) in chaotic signals
这里假定原始信号p(s)表示为101110111011010110110111010001000,此处设置状态变量信号增益J=2,噪声系数u=6,信噪比控制在[-5, 10]的范围内,可以看到经由混沌信号混合的信号p′(s)可以还原成p(s),如图12所示。

图12 信号解调前后的p(s)、p′(s)以及p″(s)Fig.12 p(s),p′(s) and p″(s) before and after signal demodulation
由图12可知,原始信号p(s)通过混合后,波长幅度增加,经过还原后,发生变换的波形p″(s)还原为p(s),即通过信号解调,混沌处理后的信号可以被还原。在信号调制过程中,信号的变换过程为:A(t)→B(t)→BC(t)→b(t)→b′(t)→e(t)→e′(t),发送信号e′(t)是由混沌信号p′(s)和高斯噪声合成的,攻击者即便拦截e′(t),如果不知道改进Logistic混沌的初值,同时又不知道该混沌系统的段函数,同时不知道子区间的峰值(B,C,D,E),就不可能解调出有意义的信号。
首先就Logistic混沌在信号保密性和信号长度分别引入多涡卷思想、压缩感知的方式,使得Logistic混沌的难度得到进一步增加,同时密码长度并没有明显增加,即保证了信号的保密性,同时并没有增加解码量,从而证明设计的改进Logistic混沌在保密通信领域是有效的。
5 结论
针对混沌密码在保密通信领域的应用,以Logistic混沌作为研究对象,针对该混沌方式存在的不足,从信号保密难度及信号长度的角度,分别引入多涡卷、压缩感知等方式,提出改进Logistic混沌的信号重构方式。相比于伯努利测量矩阵,采用本文方法进行信号重构可以取得较好的效果,同时信噪比指标出现一定幅度的提升,混沌处理后的信号增加信噪比,对应的信号误比特率明显降低,同时信号可以被还原,在改进Logistic混沌方式的信号调制下,信号难以被解码,从而证明采用该混沌方式可以提升通信信号的保密性,具有一定实用价值,今后可以在通信系统应用中做进一步的性能分析。
