最大公因数与最小公倍数方法探讨

【摘要】在求两个数的最大公因数时，新课标明确指出不再由公因数或最大公因数，引进互质数的概念，是精简数论初步知识的一个具体体现。而《标准》中有关求最大公因数的要求是：“能找出两个自然数的公因数和最大公因数”。建议学生采用“找”的方法，不再需要分解质因数与短除法。事实上，即便在过去学了分解质因数和短除法之后，也极少有学生在约分时用到。这一改进，虽说大大降低了学生学习的难度，但在教学中，笔者在课堂上和学生把其中的各种规律性知识与解决方法归拢后，很多学生对本部分的知识能够做到进一步系统化，解决方法多样化[1]。

【关键词】质数  合数  互质  质因数

【中图分类号】623.5          【文献标识码】A 【文章编号】2095-3089（2021）41-0104-02

笔者在教学过程中发现学生在寻找两个数最大公因数时，方法过于单调，几乎是机械化去找、去操作。而且在碰见一些稍复杂的因数时，往往存在丢失现象，最后导致错误连连。针对最大公因数的求法问题，笔者认为完全可以发动学生多渠道去求，不必拘泥于一标，毕竟本节内容和后面的约分、最小公倍数、通分有太多联系。联系日常教学实际，结合一些习题和资料，笔者针对本部分进行了简要梳理，期望对学有余力的孩子有所帮助，也望同行指正交流。

一、最大公因数的几条探索性规律及解决方法

1.互质的两个数最大公因数是（以下情况均是互质的情况）

（1）1与其他任意自然数互质。

（2）2和任何奇数都互质。

（3）连續的两个自然数互质。.

如：8和9;14和15;111和112……

（4）相邻的两个奇数互质。

（5）不同的两个质数互质。

如：5和7;7和19;31和89……

（6）当一个是合数，一个为质数时（合数不是质数的倍数），这两个数互质。

2.当两个数成倍数关系时，小的那个数就是这两个数的最大公因数[2]。

如：4和8;16和32……。

3.两个数的所有公因数都是最大公因数的因数（最大公因数是所有公因数的倍数）。如18与27的公因数有1、3、9。其中他们的最大公因数9也是其他公因数1、3、9的倍数。本条结论笔者认为，可以让学生以此来判断自己所找的最大公因数是否合适。

二、其实除了以上几种方法外，在寻找两数最大公因数时还可以采用以下几种方法[3]

1.列举法求18与27的最大公因数：

先分别找出18和27的因数，然后看18和27的因数中公有的部分，再从中找出最大的一个。

例如：求18与27的最大公因数。

18的因数有：1、2、3、6、9、18。

27的因数有：1、3、9、27。

18与27的公因数有：1、3、9。

18与27的最大公因数是9。

2.筛选法求18与27的最大公因数。

可以先找出18的因数，再在这些因数中圈出27的因数，进而找出两者最大的那个因数。

18的因数：①，2，③，6，⑨，18。

在18的因数中，1，3，9是27的因数，自然9是18和27的最大公因数。

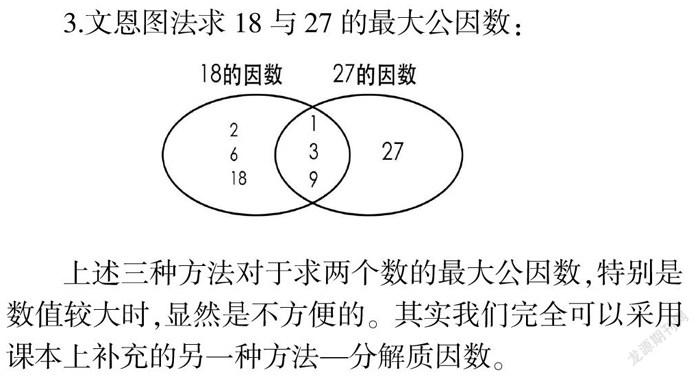
3.文恩图法求18与27的最大公因数：

上述三种方法对于求两个数的最大公因数，特别是数值较大时，显然是不方便的。其实我们完全可以采用课本上补充的另一种方法—分解质因数。

4.分解质因数法求18与27的最大公因数。

首先我们把18和27分别分解成几个质数相乘的形式，18=2×3×3，27=3×3×3。因为18和27的公因数必定包含18和27公有的质因数，而最大公因数是其中最大的一个。自然它必须包含18和27共有的质因数3与3，这样3乘3就是18和27的最大公因数。

18=2×3×3

27=3×3×3

鉴于上面的方法，我们还可以用经典的做法——短除的形式找到公因数和最大公因数。

5.短除法求18与27的最大公因数。

首先用3（18和27的最小质因数）去除这两个数，看除完的商是否互质，如果不互质，接着继续用他们的公因数（质数）往下除，一直除到商互质为止，然后把所有除数相乘，得到的积就是18和27的最大公因数。

与前边的分解质因数法相比较，我们不难发现：他们结果相同，而短除法所用到的两次除数正是这两数的公有质因数。而这两个数的最大公因数，则是这两个数的公有质因数的连乘积。无疑给学生的学习带来了一丝新意。

在通过短除法求出最大公因数9后，我们结合第三条规律——最大公因数是所有公因数的倍数（所有的公因数都是最大公因数的约数），依次求出他们的其他公因数——1，3，当然我们也可以借助短除法解决三个数或者更多数的最大公因数问题。

6.缩小倍数法求18与27的最大公因数。

当把18缩小到原来的1/2时，发现9恰好也是27的因数，通过进一步验证会发现9是18与27的最大公因数，同样的研究策略，我们可以按照相同的方法求得两个数或者三个数的最小公倍数。

虽说在教学过程中，我们不要求学生对知识过于求全求深，但作为从教者来说，让我们把知识内涵研细，研透。夯实了个人素养才会让孩子们“人人都能在数学上获得发展，不同的学生获得不同发展”。

三、结语

准确快速地求出两个数的最大公因数与最小公倍数的学习是学生很难掌握的内容，又是至关重要的。通过研究不难发现：当两数成倍数关系或互质关系时可直接写出它们的最大公因数或最小公倍数，当既要求最大公因数又要求最小公倍数时，用短除法或分解质因数法比较简便;当只求最大公因数时，用短除法或缩小倍数法比较简便;当只求最小公倍数时用大数翻倍法比较简便，当两个数比较大，比较复杂时，用短除法比较简便。

总之在探求最大公因数与最小公倍数时，需要学生看清数字之间关系，看清数据特征，看清条件与要求，用好最佳方法，认真细心计算，才能减少后期的计算迷茫。

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准[S];北京师范大学出版社，2012-1

[2]刘来刚.名师解教材 五年级数学下 人教课标改进版[M].吉林大学出版社，2011.04

[3]吴国和.求最大公因数和最小公倍数的几种方法[J].数学大世界（小学五六年级适用），2011-Z2（24）

作者简介：

胡顺治（1980年8月26日-），男，汉族，江苏省连云港市人，大学学历，一级教师（中一），研究方向：数学教育教学与班级管理。