不定方程x2+y2+z2=2(xy+yz+xz)的解及其性质
2011-04-11常秀芳
李 高,常秀芳
(山西大同大学煤炭工程学院,山西大同037003)
对于方程[1-3]

的任意一组解x=a,y=b,z=c可看成是空间一点的坐标(a,b,c)。而方程的左端总是正的,结合右端可知a,b,c同时为正,或同时为负,二者必居其一。只要把(a,b,c)写成(|a|,|b|,|c|)即同为正,为此,下面只研究正数解的情形。若(a,b,c)是方程的解,由方程的对称性知,则方程一定存在(a,c,b)、(b,a,c)、(b,c,a)、(c,a,b)、(c,b,a)的五组解,这六组解实际是坐标a,b,c的不同排列,只与坐标值有关,而与次序无关,这六组解不妨称为同组解。在同组解中,已知其中的一个,其余五组解便知。规定方程的解指的是同组解中的一个,同组解中其余五组解不作探究。
1 关于方程x2+y2+z2=2(xy+yz+xz)解的概念
1.1 邻解
若(a,b,c)是方程(1)的解,则a是方程
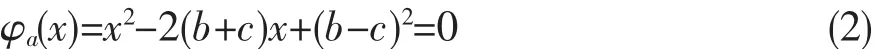
的一个根,则必存在另一个根a′,且满足
a+a′=2(b+c) aa′=(b-c)2
显然 a′>0,(a′,b,c)也是方程(1)的解,则把(a′,b,c)称为方程解(a,b,c)的a的邻解,即(a,b,c)与(a′,b,c)互为邻解。
同理,b和c也有各自的邻解(a,b′,c)和(a,b,c′)。
1.2 奇解
由于我们研究的是方程的正整数解,若有一个坐标值为零,不预考虑,应把它排除之外。为此我们规定在方程解(a,b,c)的邻解中,若有一个坐标值为零,则称(a,b,c)为方程的奇解,否则称为非奇解。
在方程解(a,b,c)中,若有两个坐标值相等,不妨b=c,可得一解(4,1,1),则称(4,1,1)为方程最简单的解。将b=c=1代入(2)式可得关于4的邻解(0,1,1),显然(4,1,1)是奇解。
1.3 互质解
方程解(a,b,c)的三个坐标中,若两两互质,则称该解为互质解。
2 关于方程x2+y2+z2=2(xy+yz+xz)解的性质
性质1 若(a,b,c)是方程的解,则(ka,kb,kc)是方程的解[4-5]
性质2若方程的解中,若有两个坐标值相等,则必得奇解,且奇解只有一个邻解。
一般地,非奇解(a,b,c)都有三个邻解(a′,b,c)、(a,b′,c)、(a,b,c′),其中 a′,b′,c′可按下式求得
a′=2(b+c)-a,b′=2(a+c)-b,c′=2(a+b)-c。
假如b=c,可得(4b,b,b),由性质1得奇解(4,1,1),又由
42+y2+12=2(4y+y+4)
得奇解(4,1,1)一邻解(4,9,1)。 该邻解(4,9,1)有除(4,1,1)外,还有(16,9,1)、(4,9,25)的邻解。
若a与b的公因子d>1,则d也是c的公因子,这与a,b,c的最大公因子为1相矛盾。故a,b,c两两互质。
性质4 互质解的邻解也是互质解。
(a,b,c)是互质解,它的三个邻解(a′,b,c)、(a,b′,c)、(a,b,c′)中,不妨设(a′,b,c)不是互质解,则 a′与b,或a′与c有公因子d>1,两者必居其一。 不妨a′与 b 有公因子 d>1,有 a′=nd,b=md。
由根与系数关系有 aa′=(b-c)2,即 aa′=and=(bc)2=(md-c)2=m2d2-2mde+c2,所以 d|c2。从而 b 与 c 有公因子 d>1,这与(a,b,c)是互质相矛盾,故(a′,b,c)是互质解。
性质5 方程互质解中,三个坐标必两奇一偶。
性质6 方程互质解(a,b,c)中,a,b,c均为平方数。
此外,每一中不同的用地类型有着不同的生境适宜性,对受生态威胁的敏感程度也不同,综合众多研究成果[26-27]的基础上,结合研究区域生态环境的具体情况,将土地利用类型分为人工地类、自然地类两大类,分别赋值0(人工)、1(自然),从人工地类到自然地类,敏感性由低到高,其取值范围为0-1,0表示不敏感,1表示高度敏感性。本文对应的地类对各威胁因子的敏感度具体如表2所示。
由方程φa(x)=x2-2(b+c)x+(b-c)2=0,φb(x)=x2-2(a+c)x+(a-c)2=0。可得
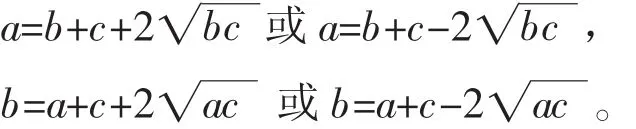
因为a,b,c是两两互质的正整数,所以a,b,c必然都是平方数。
性质7 方程非奇解(a,b,c)的三个邻解中,只有一个解的最大坐标比原来的小,另两个则具有较大的最大坐标。
不妨设 a>b>c,φa(x)=x2-2(b+c)x+(b-c)2=0 的两个根为a和a′。
因为
(b-a)(b-a′)=φa(x)=x2-2(b+c)b+(b-c)2=-c(4b-c)<0,即 b 介于 a与 a′之间,则 a>b>a′,故(a′,b,c)的最大坐标小于(a,b,c)的最大坐标。
同理,由(a-b)(a-b′)=φb(a)=a2-2(a+c)a+(a-c)2=-c(4a-c)<0 可知,a位于 b 与 b′之间,因 a>b,则 b′>a,故(a,b′,c)的最大坐标就大于(a,b,c)的最大坐标。(a,b,c′)的情况与之类似。
性质8 方程的任何一互质解都可由奇解(4,1,1)推得,即方程的任何互质解都与奇解(4,1,1)存在联系。
设(a,b,c)是方程的互质解,由性质4和性质7可知,它必有互质的邻解 (a1,b1,c1),且具有较小的最大坐标。若这个接也是非奇解,则它又能产生互质的邻解(a2,b2,c2),具有更较小的最大坐标。将这个过程继续下去,在自然数范围能从大到小是不能形成无穷递减的,所以此过程必在某个互质解具有相同坐标时停止,即该解为奇解(4,1,1)。从而从奇解(4,1,1)出发,就能逐步地并且无遗漏地得出方程的全部互质解来,再由性质2得到方程的全部解。
奇解(4,1,1)的非奇互质解是(4,9,1),而且(4,9,1)是所有非奇互质解中最小的。由非奇互质解(4,9,1)开始,每两个坐标不变,可得方程全部的互质解,如下图1所示。
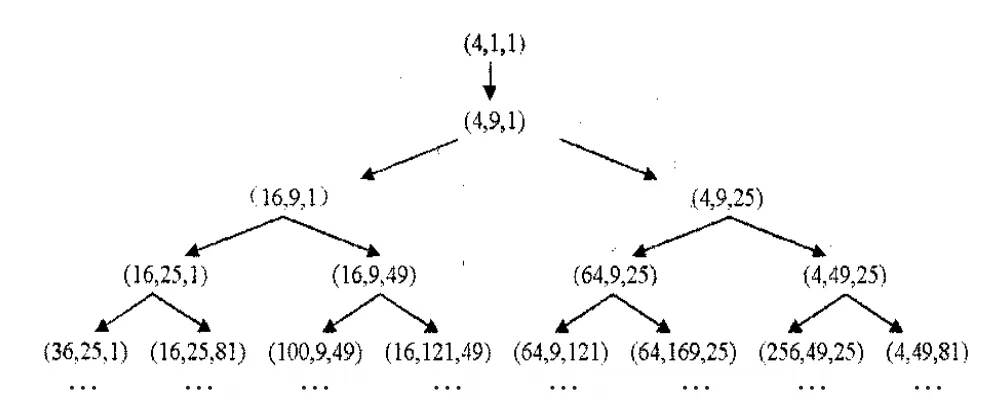
图1 方程的互质解谱树图
此图不妨称为方程的互质解谱树图,解谱树图是很容易上计算机运算的。
性质9 在解谱树图中,坐标反复轮换的一系列邻解,其坐标平方根序列中,包含着菲波纳契(Fibonacci)数列。
由性质6知,解谱树图中的任意一解的三坐标都是平方数,故解谱树图中的任一解可设为 (a2,b2,c2)的形式,则a2是二次方程
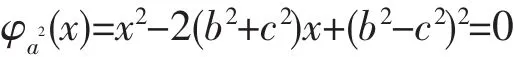
的一个根。设另一个根为a′2,有
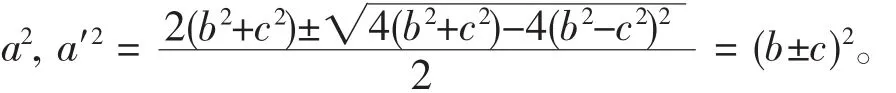
不妨令 a2=(b-c)2,a′2=(b+c)2,其中 a,a′,b,c>0,则a=b-c, a′=b+c,
同理,由方程
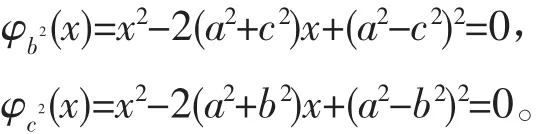
可得
b′=a+c, c′=a+b。
设(a20,b20,c20)是解谱树图中的任一解,其三坐标中两坐标不变反复轮换的一连串邻解为
(a20,b20,c20)→(a21,b20,c20)→(a21,b21,c20)→
(a21,b21,c21)→(a22,b21,c21)→(a22,b22,c21)→…
从而可得其坐标平方根序列为
a1=b0+c0b1=a1+c0=b0+2c0
c1=b1+c1=2b0+3c0a2=b1+c1=3b0+5c0
b2=a2+c1=5b0+8c0
…
令F1=b0,F2=c0,F3=a1,F4=b1,F5=c1,F6=a2,F7=b2,F8=c2,…,则有递推公式Fn=Fn-1+Fn-2。
当F1=F2=1,即b0=c0=1时,{Fn}即为菲波纳契(Fibonacci)数列。
[1]闵嗣鹤,严士健.初等数论[M].北京:高等教育出版社,1986.
[2]华罗庚.数论导引[M].北京:高等教育出版社,1957.
[3]李高,常秀芳.关于二阶变系数线性微分方程求解法的研究[J].河北北方学院学报,2010,26(6):12-14.
[4]常秀芳.掌握数学思想方法培育创新意识:以类比法为例[J].山西大同大学学报:自然科学版,2008,24(1):85-87.
[5]时宝,康淑瑰.时滞差分方程多重正周期解的存在性[J].山西大同大学学报:自然科学版,2009,25(1):1-2.
